山东省潍坊市潍城区安丘市2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列运算正确的是（　　）

A、a+a³＝a⁴ B、（a+b）²＝a²+b² C、a¹⁰÷a²＝a⁵ D、（a²）³＝a⁶

查看试题解析
2. 已知：如图，AB⊥CD于O ， EF为经过点O的一条直线，那么∠1与∠2的关系是（　　）

A、互为对顶角 B、互补 C、互余 D、相等

查看试题解析
3. 成人每天维生素D的摄入量约为0.0000046克.数据“0.0000046”用科学记数法表示为（）

A、 $46 \times 10^{- 7}$ B、 $4.6 \times 10^{- 7}$ C、 $4.6 \times 10^{- 6}$ D、 $0.46 \times 10^{- 5}$

查看试题解析
4. 如图是小希同学跳远时沙坑的示意图，测量成绩时先用皮尺从后脚印的点A处垂直拉至起跳线l的点B处，然后记录AB的长度，这样做的理由是（　　）

A、两点之间，线段最短 B、过两点有且只有一条直线 C、垂线段最短 D、过一点可以作无数条直线

查看试题解析
5. 现有四根木棒，长度分别为6cm ， 9cm ， 10cm ， 15cm ，从中任取三根木棒，能组成三角形的个数为（　　）

A、1 B、2 C、3 D、4

查看试题解析
6. 如图，可以判定AB $//$ CD的条件是（　　）

A、∠1＝∠2 B、∠BAD+∠B＝180° C、∠3＝∠4 D、∠D＝∠5

查看试题解析
7. 甲、乙两个城市，乙城市位于甲城市北偏东50°方向，距离为80km，那么甲城市位于乙城市（）

A、南偏东50°方向，距离为80km B、南偏西50°方向，距离为80km C、南偏东40°方向，距离为80km D、南偏西40°方向，距离为80km

查看试题解析
8. 下列因式分解正确的是（）

A、 $x^{2} - 2 x = x (x + 2)$ B、 $a^{2} - a - 6 = (a - 2) (a + 3)$ C、 $4 a^{2} + 4 a b - b^{2} = {(2 a - b)}^{2}$ D、 $4 x^{2} - y^{2} = (2 x + y) (2 x - y)$

查看试题解析
9. 如图，在△ABC中，点D、E、F分别是BC、AD、BE上的中点，若△ABC的面积为12cm² ，则△CEF的面积为（　　）

A、0.75 B、1.5 C、3 D、6

查看试题解析
10. 下列说法错误的是（）

A、在x轴上的点的纵坐标为0 B、点P（﹣1，3）到y轴的距离是1 C、若xy $<$ 0，x﹣y $>$ 0，那么点Q（x ， y）在第四象限 D、点A（﹣a²﹣1，|b|）一定在第二象限

查看试题解析
11. 已知a﹣b＝1，ab＝12，则a+b等于（　　）

A、7 B、5 C、±7 D、±5

查看试题解析
12. 已知关于x，y的方程组 ${\begin{cases} x + 3 y = 4 - a \\ x - y = 3 a \end{cases}$ ，给出下列结论：① ${\begin{cases} x = 5 \\ y = - 1 \end{cases}$ 是方程组的一个解；②当 $a = - 2$ 时，x，y的值互为相反数；③当 $a = 1$ 时，方程组的解也是方程 $x + y = 4 - a$ 的解；④x，y间的数量关系是 $x - 2 y = 3$ .其中正确的是（）

A、②③ B、①②③ C、②③④ D、①②③④

查看试题解析

二、填空题

13. 已知一个多边形的每个内角都是160°，则这个多边形的边数是.

查看试题解析
14. 若 $(x + 3) (x + a) = x^{2} - 2 x - 15$ ，则a= ．

查看试题解析
15. 已知 $a^{m} = 2$ ， $a^{n} = 3$ （ $m, n$ 为正整数），则 $a^{3 m + 2 n} =$ .

查看试题解析
16. 如图，将长方形纸片进行折叠，ED ， EF为折痕，A与A'、B与B'、C与C'重合，若∠AED＝25°，则∠BEF的度数为．

查看试题解析
17. 某车间 56 名工人，每人每天能生产螺栓 16 个或螺母 24 个，设有 x 名工人生产螺栓，有 y 名工人生产螺母，每天生产的螺栓和螺母按 1：2 配套，所列方程组是.

查看试题解析
18. 如图，点D是△ABC的边BC的延长线上的一点，∠ABC的平分线与∠ACD的平分线交于点A₁ ， ∠A₁BC的平分线与∠A₁CD的平分线交于点A₂ ，依此类推…，已知∠A＝α，则∠A₂₀₂₀的度数为．（用含α的代数式表示）．

查看试题解析

三、解答题

19.

(1)、因式分解：
①xy²﹣9x；

②（x﹣y）﹣2x（y﹣x）+x²（x﹣y）．

(2)、计算：
①利用乘法公式计算：2020×1980；

② ${(3 - π)}^{0} - 2^{3} + {(- 3)}^{2} - {(\frac{1}{2})}^{- 1}$ ．

查看试题解析
20. 解下列方程组：

(1)、 ${\begin{array}{l} x - 3 y = - 4 \\ \frac{x + 1}{2} + y = 1 \end{array}$ ；

(2)、 ${\begin{array}{l} \frac{x + y}{2} + \frac{x - y}{3} = 1 \\ (x + y) - 2 (x - y) = 10 \end{array}$ ．

查看试题解析
21. 化简求值：（2a+b）（2a﹣b）+b（2a+b）﹣4a² ，其中a＝﹣ $\frac{1}{2}$ ，b＝2．

查看试题解析
22. 如图，在平面直角坐标系中，O为坐标原点，点A（4，1）B（1，1），C（4，5），D（6，﹣3），E（﹣2，5）．

(1)、在坐标系中描出各点，并画出△AEC ， △BCD ．

(2)、求出△BCD的面积．

查看试题解析
23. 如图所示，点E在AB上，CE，DE分别平分∠BCD，∠ADC，∠1+∠2＝90°，∠B＝75°，求∠A的度数．

查看试题解析
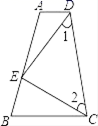24. 某生态柑橘园现有柑橘21吨，计划租用A ， B两种型号的货车将柑橘运往外地销售．已知满载时，用2辆A型车和3辆B型车一次可运柑橘12吨；用3辆A型车和4辆B型车一次可运柑橘17吨．

(1)、1辆A型车和1辆B型车满载时一次分别运柑橘多少吨？

(2)、若计划租用A型货车m辆，B型货车n辆，一次运完全部柑橘，且每辆车均为满载．
①请帮柑橘园设计租车方案；

②若A型车每辆需租金120元/次，B型车每辆需租金100元/次．请选出最省钱的租车方案，并求出最少租车费．

查看试题解析
25. 已知如图，四边形ABCD ， BE、DF分别平分四边形的外角∠MBC和∠NDC ，若∠BAD＝α，∠BCD＝β

(1)、如图1，若α+β＝150°，求∠MBC+∠NDC的度数；

(2)、如图1，若BE与DF相交于点G ， ∠BGD＝45°，请写出α、β所满足的等量关系式；

(3)、如图2，若α＝β，判断BE、DF的位置关系，并说明理由．

查看试题解析