山东省威海市文登区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列方程是二元一次方程的是( )A、 B、 C、 D、2. 一个事件的概率不可能是( )A、1.5 B、1 C、0.5 D、03. 下列成语描述的事件是必然事件的是( )A、守株待兔 B、翁中捉鳖 C、画饼充饥 D、水中捞月4. 已知方程组 ,则 的值为( )A、 B、 C、 D、5. 如图, ,下列结论正确的是( )
 A、 B、 C、 D、6. 某商场开业举行庆祝活动,凡是到商场的人均可参加“意外惊喜”的游戏,游戏规则为:一个袋中装有白球和红球共 个(些小球除颜色外都相同),任意摸出一个球,如果摸到红球就可获得商场免费提供的一份礼品.据统计,当天参加活动的人数约 人,商场发放了 份礼品,试估计袋中红球的个数为( )A、 B、 C、 D、7. 如果 ,则下列各式不成立的是( )A、 B、 C、 D、8. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中n的值可以是( ).A、 B、 C、 D、9. 小明、小颖、小亮玩飞镖游戏,他们每人投靶 次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分 分,小亮得分 分,则小颖得分为( )
A、 B、 C、 D、6. 某商场开业举行庆祝活动,凡是到商场的人均可参加“意外惊喜”的游戏,游戏规则为:一个袋中装有白球和红球共 个(些小球除颜色外都相同),任意摸出一个球,如果摸到红球就可获得商场免费提供的一份礼品.据统计,当天参加活动的人数约 人,商场发放了 份礼品,试估计袋中红球的个数为( )A、 B、 C、 D、7. 如果 ,则下列各式不成立的是( )A、 B、 C、 D、8. 判断命题“如果 ,那么 ”是假命题,只需举出一个反例,反例中n的值可以是( ).A、 B、 C、 D、9. 小明、小颖、小亮玩飞镖游戏,他们每人投靶 次,中靶情况如图所示.规定投中同一圆环得分相同,若小明得分 分,小亮得分 分,则小颖得分为( ) A、 分 B、 分 C、 分 D、 分10. 已知 ,按照以下步骤作图:①分别以点B,C为圆心,以大于 的长为半径画弧,两弧交于点M,N;②作直线 交 于点D,连接 .若 , ,下列结论错误的是( )
A、 分 B、 分 C、 分 D、 分10. 已知 ,按照以下步骤作图:①分别以点B,C为圆心,以大于 的长为半径画弧,两弧交于点M,N;②作直线 交 于点D,连接 .若 , ,下列结论错误的是( ) A、 B、 C、 D、11. 若不等式组 有解,则m的取值范围为( )A、 B、 C、 D、12. 某快递公司每天上午 为集中件和派件时段,甲仓库用来揽收快件,乙仓库用来派发件快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:① 分钟后,甲仓库内快件数量为 件;②乙仓库每分钟派送快件数量为 件:③ 时,甲仓库内快件数为 件;④ 时,两仓库快递件数相同( )
A、 B、 C、 D、11. 若不等式组 有解,则m的取值范围为( )A、 B、 C、 D、12. 某快递公司每天上午 为集中件和派件时段,甲仓库用来揽收快件,乙仓库用来派发件快件,该时段内甲、乙两仓库的快件数量y(件)与时间x(分)之间的函数图象如图所示,下列说法正确的个数为:① 分钟后,甲仓库内快件数量为 件;②乙仓库每分钟派送快件数量为 件:③ 时,甲仓库内快件数为 件;④ 时,两仓库快递件数相同( ) A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
13. 点 在第四象限,则m的取值范围是 .14. 一个小球在如图所示的地板上自由滚动,最终停在阴影区域的概率为.
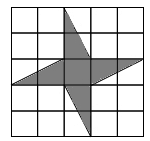 15. 如图, ,若 , ,则 .
15. 如图, ,若 , ,则 . 16. 某品牌电脑,成本价 元,售价 元,现打折销售,要使利润率不低于 ,最低可以打折.17. 如图, +∠G= .
16. 某品牌电脑,成本价 元,售价 元,现打折销售,要使利润率不低于 ,最低可以打折.17. 如图, +∠G= .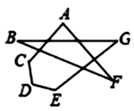 18. 如图, 中, 的角平分线 和 边的中垂线 交于点D, 的延长线于点M, 于点N.若 , ,则 的长为 .
18. 如图, 中, 的角平分线 和 边的中垂线 交于点D, 的延长线于点M, 于点N.若 , ,则 的长为 .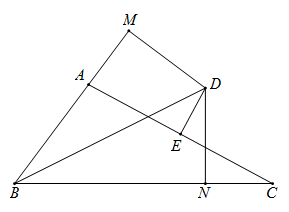
三、解答题
-
19.(1)、解不等式组,并将解集在数轴上表示出来:(2)、关于x,y的方程组 的解x与y的值互为相反数,求m的值.20. 如图, , .

求证: .(请注明每一步的推理依据)
21. 七年级(1)班的同学分成男生女生两个组做游戏.现有长度分别为 , 的两根小木棒和一个被平均分成 份的转盘,转盘上标有数字 , , , .游戏规则如下:每个小组分别派出一名代表各转动转盘一次,指针指向的数字作为第三根小木棒的长度.若三根小木棒能够组成三角形,则女生获胜;若三根小木棒能够组成等腰三角形,则男生获胜. (1)、这个游戏对谁有利?请说明理由;(2)、请只改动转盘上一个数字,使游戏公平:将数字改成 .22. 如图,一次函数 经过点 ,与一次函数 交于点 .
(1)、这个游戏对谁有利?请说明理由;(2)、请只改动转盘上一个数字,使游戏公平:将数字改成 .22. 如图,一次函数 经过点 ,与一次函数 交于点 . (1)、求函数 的表达式;(2)、利用函数图象写出方程组 的解 .23. 在抗击新冠肺炎疫情期间,各省市积极组织医护人员支援武汉.某市组织医护人员统一乘车去武汉,若单独调配45座客车若辆,则有15人没有座位;若只调配30座客车,则用车数量将增加3辆,并空出15个座位.(1)、该市有多少医护人员支援武汉?(2)、若同时调配 座和 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?
(1)、求函数 的表达式;(2)、利用函数图象写出方程组 的解 .23. 在抗击新冠肺炎疫情期间,各省市积极组织医护人员支援武汉.某市组织医护人员统一乘车去武汉,若单独调配45座客车若辆,则有15人没有座位;若只调配30座客车,则用车数量将增加3辆,并空出15个座位.(1)、该市有多少医护人员支援武汉?(2)、若同时调配 座和 座两种车型,既保证每人有座,又保证每车不空座,则两种车型各需多少辆?

