山东省青岛市西海岸新区、黄岛区2019-2020学年七年级下学期数学期末试卷
试卷更新日期：2021-04-28 类型：期末考试
一、单选题
-
1. 下列交通指示标识中，是轴对称图形的有（ ）
A、1个 B、2个 C、3个 D、4个2. 已知一个三角形两边的长分别是5和7，则此三角形第三边的长不可能是（ ）A、2 B、5 C、7 D、103. 下列计算正确的是（ ）A、 B、 C、 D、4. 甲、乙两位同学在一次实验中统计了某一结果出现的频率，给出的统计图如图所示，则符合这一结果的实验可能是（ ）
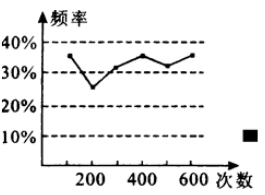A、掷一枚正六面体的骰子，出现5点的概率 B、掷一枚硬币，出现正面朝上的概率 C、任意写出一个整数，能被2整除的概率 D、一个袋子中装着只有颜色不同，其他都相同的 两个红球和一个黄球，从中任意取出一个是黄球的概率5. 如图，直线 ，点A在直线 上，以点A为圆心，适当长度为半径画弧，分别交直线 、 于B、C两点，连结AC、BC.若 ，则 的大小为（ ）
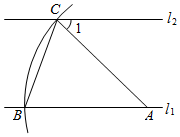A、 B、 C、 D、6. 如图，在 中， 是 上的任意两点．若 ，则图中阴影部分的面积为（ ）
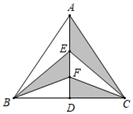A、12 B、20 C、24 D、487. 在正方形方格纸中，每个小方格的顶点叫做格点，以格点的连线为边的三角形叫做格点三角形．如图是5×5的正方形方格纸，以点D，E为两个顶点作格点三角形，使所作的格点三角形与△ABC全等，这样的格点三角形最多可以画出（ ）
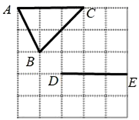A、2个 B、4个 C、6个 D、8个8. 如图，在长方形 中，动点P从A出发，以相同的速度，沿 方向运动到点A处停止．设点P运动的路程为 的面积为y，如果y与x之间的关系如图所示，那么长方形 的面积为（ ）
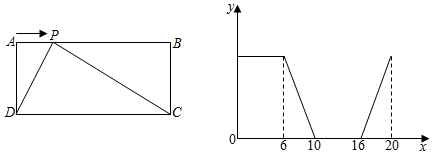A、12 B、24 C、20 D、48二、填空题
-
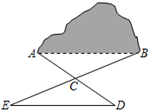
9. 3D打印技术日渐普及，打印出的高精密游标卡尺误差只有±0.000 063米.0.000 063这个数用科学记数法可以表示为 ．10. 如图，有一座小山，现要在小山A ， B的两端开一条隧道，施工队要知道A ， B两端的距离，于是先在平地上取一个可以直接到达点A和点B的点C ， 连接AC并延长到D ， 使CD＝CA ， 连接BC并延长到E ， 使CE＝CB ， 连接DE ． 经测量DE ， EC ， DC的长度分别为800 m，500 m，400 m，则A ， B之间的距离为m．
11. 某商场为了吸引更多的顾客，安排了一个抽奖活动，并规定：顾客每购买100元商品，就能获得一次抽奖的机会．抽奖规则如下：在抽奖箱内，有100个牌子，分别写有1，2，3，．.100这100个数，抽到末位数字是5的可获得20元购物券，抽到数是88的可获得200元购物券，抽到数是66或99的可获得100元购物券，某顾客购物130元，他获得购物券的概率是 ．12. 如图，在等边三角形网格中，已有两个小等边三角形被涂黑，若再将图中其余小等边三角形涂黑一个，使涂色部分构成一个轴对称图形，则有种不同的涂法．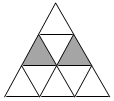
13. 如图， 平分 ，若 ，则 ．
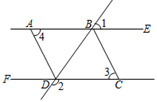14. 如图，如果小球在用七巧板拼成的正方形中自由地滚动，并随机地停留在某区域，它最终停留在5号区域的概率为 ．
15. 如图，在△ABC中，AB=AC=8cm，BC=5cm．D、E分别是AB、AC边上的点，将△ADE沿直线DE折叠，点A落在点A′的位置，点A′在△ABC的外部，则阴影部分图形的周长为cm．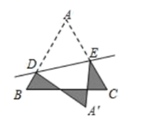
16. 一根绳子弯曲成如图1所示的形状．当用剪刀像图2那样沿虚线把绳子剪断时，绳子被剪为5段；当用剪刀像图3那样沿虚线 把绳子再剪一次时，绳子就被剪为9段；若用剪刀在虚线 之间把绳子再剪若干次（剪刀的方向与a平行）．按上述规律用剪刀一共剪2020次时绳子的段数是 ．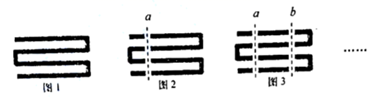
三、解答题
-
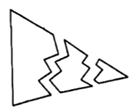
17. 如图，小明不慎将一块三角形模具打碎为三块，请利用学过的知识画出一个与原来三角形模具一样的三角形．
18. 计算：(1)、﹣14+（﹣2）3+（π﹣3.14）0+（﹣ ）﹣2；(2)、（﹣a）3•a5+（﹣4a4）2；(3)、（3ab3﹣a2b+ ab）÷（﹣ ab）；(4)、先化简，再求值：（2a﹣b）2+（a+1﹣b）（a+1+b）﹣（a+1）2 ， 其中a＝ ，b＝﹣2．19. 如图，已知BE∥FG，∠1＝∠2，∠ABC＝40°，试求∠ADE的度数．
20. 在一个口袋中装有4个红球和8个白球，它们除颜色外完全相同．(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件，并写出其发生的概率；(2)、求从口袋中随机摸出一个球是红球的概率；；(3)、现从口袋中取走若干个白球，并放入相同数量的红球，充分摇匀后，要使从中随机摸出一个球是红球的概率是 ，问取走了多少个白球？21. 如图，AB//CD，∠B＝∠D，O是CD的中点，连接AO并延长，交BC的延长线于点E.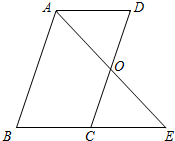
(1)、试判断AD与BE有怎样的位置关系，并说明理由；(2)、试说明△AOD≌△EOC.22. 甲、乙两个批发店销售同一种苹果．在甲批发店，不论购买数量是多少，价格均为6元/千克，在乙批发店，购买数量不越过50千克时，价格为7元千克；购买数超过50千克时，超出部分的价格为5元千克．假设小王在某批发店购买苹果的数为x千克 ．(1)、根据题意填表：购买数量/千克
30
50
150
…
甲批发店费用/元
300
…
乙批发店费用/元
350
…
(2)、假设在甲批发店购买苹果的费用为y元，求y与x之间的关系式；(3)、根据题意填空①若小王在甲、乙两个批发店购买的苹果的数量相同．且花费也相同，则他购买的苹果的数量为千克；
②若小王计划购买的苹果的数量为120千克，则他去批发店购买时的花费少；
③若小王购买苹果时花费了360元，则他去批发店购买的数量多．
23. 若一个两位数十位、个位上的数字分别为m ， n ， 我们可将这个两位数记为 ，易知 =10m+n；同理，一个三位数、四位数等均可以用此记法，如 =100a+10b+c ．(1)、（基础训练）解方程填空：
①若 + =45，则x=；
②若 – =26，则y=；
③若 + = ，则t=；
(2)、（能力提升）交换任意一个两位数 的个位数字与十位数字，可得到一个新数 ，则 + 一定能被整除， – 一定能被整除， • –mn一定能被整除；（请从大于5的整数中选择合适的数填空）
(3)、（探索发现）北京时间2019年4月10日21时，人类拍摄的首张黑洞照片问世，黑洞是一种引力极大的天体，连光都逃脱不了它的束缚．数学中也存在有趣的黑洞现象：任选一个三位数，要求个、十、百位的数字各不相同，把这个三位数的三个数字按大小重新排列，得出一个最大的数和一个最小的数，用得出的最大的数减去最小的数得到一个新数（例如若选的数为325，则用532–235=297），再将这个新数按上述方式重新排列，再相减，像这样运算若干次后一定会得到同一个重复出现的数，这个数称为“卡普雷卡尔黑洞数”．
①该“卡普雷卡尔黑洞数”为 ▲ ；
②设任选的三位数为 （不妨设a＞b＞c），试说明其均可产生该黑洞数．
24. 如图，在 ABC中，∠ACB＝90°，AC＝BC，AB＝8cm，过点C作射线CD，且CD∥AB，点P从点C出发，沿射线CD方向匀速运动，速度为3cm/s；点Q从点A出发，沿AB边向点B匀速运动，速度为1cm/s，当点Q停止运动时，点P也停止运动．连接PQ，CQ，设动点的运动时间为t（s）（0＜t＜8），解答下列问题：
(1)、用含有t的代数式表示CP和BQ的长度；(2)、当t＝2时，请说明PQ∥BC；(3)、设 的面积为S（cm2），求S与t之间的关系式．