山东省青岛市市北区2019-2020学年七年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列事件为必然事件的是（）

A、射击一次，中靶 B、画一个三角形，其内角和是 $180 °$ C、掷一枚质地均匀的硬币，正面朝上 D、12人中至少有2人的生日在同一个月

查看试题解析
2. 下列运算正确的是（）

A、a²⋅a³=a⁶ B、a⁵+a³=a⁸ C、（a⁴）²=a⁶ D、a⁵÷a⁵=1（a≠0）

查看试题解析
3. 下面图标中，是轴对称图形的是（）

A、 B、 C、 D、

查看试题解析
4. 用三角板作 $△ A B C$ 的边 $A C$ 上的高，下列三角板的摆放位置正确的是（）

A、 B、 C、 D、

查看试题解析
5. 下面四个实验中，实验结果概率最小的是（）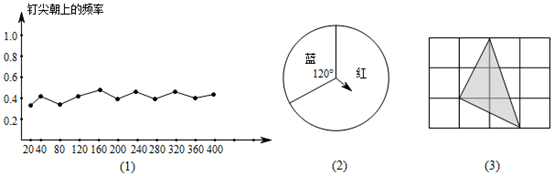

A、如（1）图，在一次实验中，老师共做了400次掷图钉游戏，并记录了游戏的结果绘制了下面的折线统计图，估计出的钉尖朝上的概率 B、如（2）图，是一个可以自由转动的转盘，任意转动转盘，当转盘停止时，指针落在蓝色区域的概率 C、如（3）图，有一个小球在的地板上自由滚动，地板上的每个格都是边长为1的正方形，则小球在地板上最终停留在黑色区域的概率 D、有7张卡片，分别标有数字1，2，3，4，6，8，9，将它们背面朝上洗匀后，从中随机抽出一张，抽出标有数字“大于6”的卡片的概率

查看试题解析
6. 如图所示的正方形网格中，网格线的交点为格点，已知A，B是两个定格点，如果C也是图中的格点，且使得 $△ A B C$ 为等腰三角形，则点C的个数是（）

A、6个 B、7个 C、8个 D、9个

查看试题解析
7.
下列各情景分别可以用哪一幅图来近似的刻画？正确的顺序是（　　）
①汽车紧急刹车（速度与时间的关系）
②人的身高变化（身高与年龄的关系）
③跳过运动员跳跃横杆（高度与时间的关系）
④一面冉冉上升的红旗（高度与时间的关系）

A、abcd B、dabc C、dbca D、cabd

查看试题解析
8. 乐乐观察“抖空竹“时发现，可以将某一时刻的情形抽象成数学问题：如图，已知AB∥CD，∠BAE＝92°，∠DCE＝115°，则∠E的度数是（）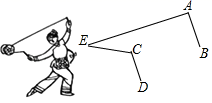

A、32° B、28° C、26° D、23°

查看试题解析

二、填空题

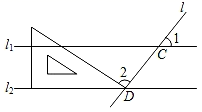
9. 小颖已有两根长度分别为 $5 c m$ 、 $7 c m$ 的木棒，再给一根多长的木棒，能方便她把三根木棒首尾相接摆成一个三角形？请你提供一个合适的木棒长度，你提供的长度是 $c m$ ．

查看试题解析
10. 生物学家发现了一种病毒，其长度约为 0.0000000052mm，数据 0.0000000052 用科学记数法表示为．

查看试题解析
11. 如图，直线l₁//l₂ ，且分别与直线l交于C，D两点，把一块含30°角的三角尺按如图所示的位置摆放，若∠1＝58°，则∠2的度数为．

查看试题解析
12. 如图，已知 $△ A B C$ 的两条边 $A C = 8$ ， $B C = 6$ ，现将 $△ A B C$ 沿 $D E$ 折叠，使点A与点B重合，则 $△ B C E$ 的周长是．

查看试题解析
13. 如图，直线 $l_{1} / / l_{2}$ ，以直线 $l_{1}$ 上的点A为圆心，适当长为半径在右侧画弧，分别交 $l_{1}$ ， $l_{2}$ 于点 $B ， C$ ．连结 $A C$ ， $B C$ ．若 $∠ 1 = 56 °$ ，则 $∠ A B C$ 的度数是．

查看试题解析
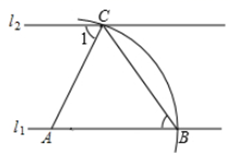14. 把一幅七巧板按如图所示进行①～⑦编号，①～⑦号分别对应着七巧板的七块，如果编号④对应的面积等于4，则由这幅七巧板拼得的“天鹅”的面积等于．

查看试题解析
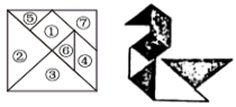15. 用每片长6cm的纸条，重叠1cm粘贴成一条纸带，如图．纸带的长度y（cm）与纸片的张数x之间的函数关系式是

查看试题解析
16. 如图，P为 $∠ M O N$ 内部的已知点，连接 $O P$ ，A为 $O M$ 上的点，B为 $O N$ 上的点，当 $Δ P A B$ 周长的最小值与 $O P$ 的长度相等， $∠ M O N$ 的度数为 $°$ ．

查看试题解析

三、解答题

17. 如图，已知点M、N和∠AOB，求作一点P，使P到点M、N的距离相等，且到∠AOB的两边的距离相等．(尺规作图，保留作图痕迹，不写作法)

查看试题解析
18. 计算：

(1)、计算： ${(- 2020)}^{0} - {(\frac{1}{3})}^{- 1}$

(2)、计算： ${(- a^{2} b)}^{2} \cdot 2 a b \div (- 3 a b^{3})$

(3)、计算： ${(2 x + 1)}^{2} - 4 (x - 1) (x + 1)$

(4)、运用乘法公式计算： $123^{2} - 122 \times 124$

(5)、先化简，再求值： ${(x - 2 y)}^{2} - x (x + 3 y) - 4 y^{2}$ ，其中 $x = - 4$ ， $y = \frac{1}{2}$

查看试题解析
19. 按逻辑填写步骤和理由：如图，a∥b，点A在直线a上，点B、C在直线b上，且 $B A ⊥ C A$ ，点D在线段 $B C$ 上，连接 $A D$ ，且 $A C$ 平分 $∠ D A F$ ．请证明： $∠ 3 = ∠ 5$ ．

证明：∵ $B A ⊥ C A$ （已知）

∴ $∠ B A C = ∠ 2 + ∠ 3 = 90 °$ （    ▲    ）

∵ $∠ 1 + ∠ B A C + ∠ 4 = 180 °$ （平角的定义）

∴ $∠ 1 + ∠ 4 = 180 ° - ∠ B A C = 180 ° - 90 ° = 90 °$

∵ $A C$ 平分 $∠ D A F$ （已知）

∴ $∠ 1 =$     ▲    （    ▲    ）

∴ $∠ 3 = ∠ 4$ （    ▲    ）

∵ $a$ ∥ $b$ （已知）

∴ $∠ 4 = ∠ 5$ （    ▲    ）

∴ $∠ 3 = ∠ 5$ （    ▲    ）

查看试题解析
20. “五·一”期间，某书城为了招徕顾客，设立了一个可以自由转动的转盘（如图，转盘被平均分成12份），并规定：读者每购买100元图书，就可获得一次转动转盘的机会，如果转盘停止后，指针正好对准红色、黄色、绿色区域，那么读者就可以分别获得45元、30元、25元的购书券，凭购书券可以在书城继续购书．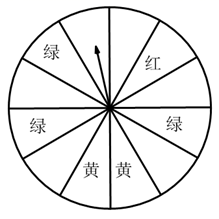

(1)、写出任意转动一次转盘获得购书券的概率；

(2)、写出任意转动一次转盘获得45元，30元，25元的概率．

查看试题解析
21. 小明家距离学校8千米，今天早晨，小明骑车上学图中，自行车出现故障，恰好路边有便民服务点，几分钟后车修好了，他以更快的速度匀速骑车到校.我们根据小明的这段经历画了一幅图象（如图），该图描绘了小明行驶的路程（千米）与他所用的时间（分钟）之间的关系.请根据图象，解答下列问题：

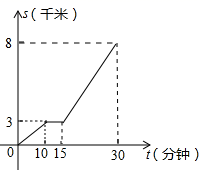(1)、小明行了多少千米时，自行车出现故障？修车用了几分钟？

(2)、小明从早晨出发直到到达学校共用了多少分钟？

(3)、小明修车前、后的行驶速度分别是多少？

(4)、如果自行车未出现故障，小明一直用修车前的速度行驶，那么他比实际情况早到或晚到多少分钟？

查看试题解析
22. 如图，已知：点 $E ， D ， B ， F$ 在同一条直线上，AD∥CB， $∠ B A D = ∠ B C D$ ， $D E = B F$ ．

(1)、判断线段 $A D$ 与 $B C$ 的数量关系，并说明理由；

(2)、判断线段 $A E$ 与 $C F$ 的位置关系，并说明理由．

查看试题解析
23. 数形结合是解决数学问题的一种重要的思想方法，借助图的直观性，可以帮助理解数学问题．

(1)、请写出图1、图2、图3分别能解释的乘法公式．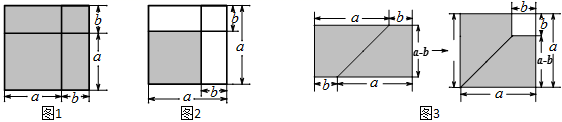

(2)、用4个全等的长和宽分别为a、b的长方形拼摆成一个如图4的正方形，请你写出这三个代数式 ${(a + b)}^{2}$ 、 ${(a - b)}^{2}$ 、 $a b$ 之间的等量关系．

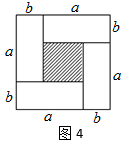(3)、根据（2）中你探索发现的结论，完成下列问题：
①当 $a + b = 5$ ， $a b = - 6$ 时，则 $a - b$ 的值为▲ ．

②设 $A = \frac{x + 2 y - 3}{4}$ ， $B = x - 2 y - 3$ ，计算： ${(A + B)}^{2} - {(A - B)}^{2}$ 的结果．

查看试题解析
24.

(1)、阅读理解：如图1，以 $△ A B C$ 的边 $A B$ 、 $A C$ 分别向外作等腰直角 $△ A B D$ 与等腰直角 $△ A C E$ ， $∠ B A D = ∠ C A E = 90 °$ ，连接 $B E$ 和 $C D$ 并相交于点O， $A B$ 与 $C D$ 相交于点F， $A C$ 与 $B E$ 相交于点G，试探究线段 $B E$ 与 $D C$ 的数量和位置关系．请将以下的探究和推理过程补充完整．

∵ $△ A B D$ 和 $△ A C E$ 都是等腰直角三角形（已知）

∴ $A B = A D$ ， $A E = A C$ （等腰直角三角形定义）

又∵ $∠ B A D = ∠ C A E = 90 °$ （已知）

∴ $∠ B A D + ∠ B A C =$ （等式性质）

即：

∴ $△ A B E ≌ △ A D C$ （）

∴ $B E = D C$ （全等三角形的对应边相等）

$∠ A B E = ∠ A D C$ （全等三角形的对应角相等）

又∵ $∠ B F O = ∠ D F A$ （）

$∠ A D F + ∠ D F A = 90 °$ （直角三角形的两个锐角互余）

∴ $∠ A B E + ∠ B F O = 90 °$ （等量代换）

∴ ， ∴ $B E ⊥ D C$ ．

(2)、拓展探究：如图2，若以 $△ A B C$ 的边 $A B$ 、 $A C$ 分别向外作等边 $△ A B D$ 与等边 $△ A C E$ ，连接 $B E$ 和 $C D$ ，并相交于点O， $A B$ 交 $C D$ 于点F， $A C$ 交 $B E$ 于G．

①线段 $B E$ 与 $D C$ 还相等吗？请说明理由；

②求 $∠ B O D$ 的度数．

查看试题解析