山东省青岛市李沧区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列图案中,是轴对称图形的有( )
 A、1个 B、2个 C、3个 D、4个2. 已知一个三角形两边的长分别是5和7,则此三角形第三边的长不可能是( )A、2 B、5 C、7 D、103. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率,并绘出了如下统计图,则符合这一结果的实验可能是( )
A、1个 B、2个 C、3个 D、4个2. 已知一个三角形两边的长分别是5和7,则此三角形第三边的长不可能是( )A、2 B、5 C、7 D、103. 下列计算正确的是( )A、 B、 C、 D、4. 甲、乙两位同学在一次用频率估计概率的实验中统计了某一结果出现的频率,并绘出了如下统计图,则符合这一结果的实验可能是( )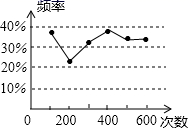 A、掷一枚正六面体的骰子,出现5点的概率 B、掷一枚硬币,出现正面朝上的概事 C、一个不透明的袋子中装着除颜色外都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 D、任意写出一个两位数,能被2整除的概率5. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )
A、掷一枚正六面体的骰子,出现5点的概率 B、掷一枚硬币,出现正面朝上的概事 C、一个不透明的袋子中装着除颜色外都相同的两个红球和一个黄球,从中任意取出一个是黄球的概率 D、任意写出一个两位数,能被2整除的概率5. 如图,直线 ,点A在直线 上,以点A为圆心,适当长度为半径画弧,分别交直线 、 于B、C两点,连结AC、BC.若 ,则 的大小为( )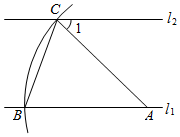 A、 B、 C、 D、6. 如图,在 中, 是 上的任意两点.若 ,则图中阴影部分的面积为( )
A、 B、 C、 D、6. 如图,在 中, 是 上的任意两点.若 ,则图中阴影部分的面积为( )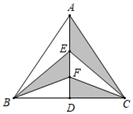 A、12 B、20 C、24 D、487. 在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )
A、12 B、20 C、24 D、487. 在正方形方格纸中,每个小方格的顶点叫做格点,以格点的连线为边的三角形叫做格点三角形.如图是5×5的正方形方格纸,以点D,E为两个顶点作格点三角形,使所作的格点三角形与△ABC全等,这样的格点三角形最多可以画出( )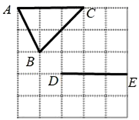 A、2个 B、4个 C、6个 D、8个8. 如图,在长方形 中,动点P从A出发,以相同的速度,沿 方向运动到点A处停止.设点P运动的路程为 的面积为y,如果y与x之间的关系如图所示,那么长方形 的面积为( )
A、2个 B、4个 C、6个 D、8个8. 如图,在长方形 中,动点P从A出发,以相同的速度,沿 方向运动到点A处停止.设点P运动的路程为 的面积为y,如果y与x之间的关系如图所示,那么长方形 的面积为( )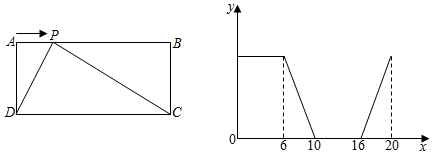 A、12 B、24 C、20 D、48
A、12 B、24 C、20 D、48二、填空题
-
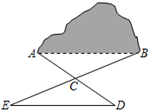
9. 3D打印技术日渐普及,打印出的高精密游标卡尺误差只有±0.000 063米.0.000 063这个数用科学记数法可以表示为 .10. 如图,有一座小山,现要在小山A , B的两端开一条隧道,施工队要知道A , B两端的距离,于是先在平地上取一个可以直接到达点A和点B的点C , 连接AC并延长到D , 使CD=CA , 连接BC并延长到E , 使CE=CB , 连接DE . 经测量DE , EC , DC的长度分别为800 m,500 m,400 m,则A , B之间的距离为m.
 11. 某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,..100这100个数,抽到末位数字是5的可获得20元购物券,抽到数是88的可获得200元购物券,抽到数是66或99的可获得100元购物券,某顾客购物130元,他获得购物券的概率是 .12. 如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同的涂法.
11. 某商场为了吸引更多的顾客,安排了一个抽奖活动,并规定:顾客每购买100元商品,就能获得一次抽奖的机会.抽奖规则如下:在抽奖箱内,有100个牌子,分别写有1,2,3,..100这100个数,抽到末位数字是5的可获得20元购物券,抽到数是88的可获得200元购物券,抽到数是66或99的可获得100元购物券,某顾客购物130元,他获得购物券的概率是 .12. 如图,在等边三角形网格中,已有两个小等边三角形被涂黑,若再将图中其余小等边三角形涂黑一个,使涂色部分构成一个轴对称图形,则有种不同的涂法.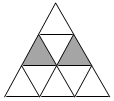 13. 如图, 平分 ,若 ,则 .
13. 如图, 平分 ,若 ,则 .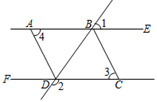 14. 如图,如果小球在用七巧板拼成的正方形中自由地滚动,并随机地停留在某区域,它最终停留在5号区域的概率为 .
14. 如图,如果小球在用七巧板拼成的正方形中自由地滚动,并随机地停留在某区域,它最终停留在5号区域的概率为 . 15. 如图,在△ABC中,AB=AC=8cm,BC=5cm.D、E分别是AB、AC边上的点,将△ADE沿直线DE折叠,点A落在点A′的位置,点A′在△ABC的外部,则阴影部分图形的周长为cm.
15. 如图,在△ABC中,AB=AC=8cm,BC=5cm.D、E分别是AB、AC边上的点,将△ADE沿直线DE折叠,点A落在点A′的位置,点A′在△ABC的外部,则阴影部分图形的周长为cm.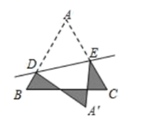 16. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线 把绳子再剪一次时,绳子就被剪为9段;若用剪刀在虚线 之间把绳子再剪若干次(剪刀的方向与a平行).按上述规律用剪刀一共剪2020次时绳子的段数是 .
16. 一根绳子弯曲成如图1所示的形状.当用剪刀像图2那样沿虚线把绳子剪断时,绳子被剪为5段;当用剪刀像图3那样沿虚线 把绳子再剪一次时,绳子就被剪为9段;若用剪刀在虚线 之间把绳子再剪若干次(剪刀的方向与a平行).按上述规律用剪刀一共剪2020次时绳子的段数是 .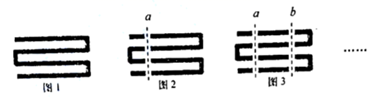 17. 若一个两位数十位、个位上的数字分别为 ,我们可将这个两位数记为 ,易知 ;同理,一个三位数、四位数等均可以用此记法,如 ,
17. 若一个两位数十位、个位上的数字分别为 ,我们可将这个两位数记为 ,易知 ;同理,一个三位数、四位数等均可以用此记法,如 ,(基础训练)
(1)、①若 ,则 ;②若 ,则 ;
③若 ,则 .
(2)、(能力提升)交换任意一个两位数 的个位数字与十位数字,可得到一个新两位数 ,则 一定能被整除, 一定能被整除.(请从大于5的整数中选择合适的数填空)
(3)、(探索发现)北京时间2019年4月10日21时,人类拍摄的首张黑洞照片问世,黑洞是一种引力极大的天体,连光都逃脱不了它的束缚.数学中也存在有趣的黑洞现象:任选一个三位数,要求个、十、百位的数字各不相同,把这个三位数的三个数字按大小重新排列,得出一个最大的数和一个最小的数,用得出的最大的数减去最小的数得到一个新数(例如若选的数为325,则用 ),再将这个新数按上述方式重新排列,再相减,像这样运算若干次后一定会得到同一个重复出现的数,这个数称为“卡普雷卡尔黑洞数”.则该“卡普雷卡尔黑洞数”为 .
三、解答题
-
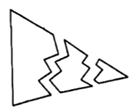
18. 如图,小明不慎将一块三角形模具打碎为三块,请利用学过的知识画出一个与原来三角形模具一样的三角形.
 19. 计算(1)、(2)、(3)、(4)、先化简,再求值: ,其中 .20. 如图,已知 ,试求 的度数.
19. 计算(1)、(2)、(3)、(4)、先化简,再求值: ,其中 .20. 如图,已知 ,试求 的度数.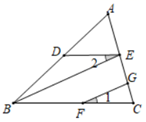 21. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?22. 如图,AB//CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.
21. 在一个口袋中装有4个红球和8个白球,它们除颜色外完全相同.(1)、判断事件“从口袋中随机摸出一个球是黑球”是什么事件,并写出其发生的概率;(2)、求从口袋中随机摸出一个球是红球的概率;;(3)、现从口袋中取走若干个白球,并放入相同数量的红球,充分摇匀后,要使从中随机摸出一个球是红球的概率是 ,问取走了多少个白球?22. 如图,AB//CD,∠B=∠D,O是CD的中点,连接AO并延长,交BC的延长线于点E.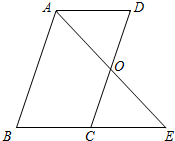 (1)、试判断AD与BE有怎样的位置关系,并说明理由;(2)、试说明△AOD≌△EOC.23. 甲、乙两个批发店销售同一种苹果.在甲批发店,不论购买数量是多少,价格均为6元/千克,在乙批发店,购买数量不越过50千克时,价格为7元千克;购买数超过50千克时,超出部分的价格为5元千克.假设小王在某批发店购买苹果的数为x千克 .(1)、根据题意填表:
(1)、试判断AD与BE有怎样的位置关系,并说明理由;(2)、试说明△AOD≌△EOC.23. 甲、乙两个批发店销售同一种苹果.在甲批发店,不论购买数量是多少,价格均为6元/千克,在乙批发店,购买数量不越过50千克时,价格为7元千克;购买数超过50千克时,超出部分的价格为5元千克.假设小王在某批发店购买苹果的数为x千克 .(1)、根据题意填表:购买数量/千克
30
50
150
…
甲批发店费用/元
300
…
乙批发店费用/元
350
…
(2)、假设在甲批发店购买苹果的费用为y元,求y与x之间的关系式;(3)、根据题意填空①若小王在甲、乙两个批发店购买的苹果的数量相同.且花费也相同,则他购买的苹果的数量为千克;
②若小王计划购买的苹果的数量为120千克,则他去批发店购买时的花费少;
③若小王购买苹果时花费了360元,则他去批发店购买的数量多.
24. 如图,在 中, ,过点C做射线 ,且 ,点P从点C出发,沿射线 方向均匀运动,速度为 ;同时,点Q从点A出发,沿 向点B匀速运动,速度为 ,当点Q停止运动时,点P也停止运动.连接 ,设运动时间为 .解答下列问题: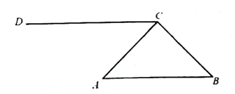
 (1)、用含有t的代数式表示 和 的长度;(2)、当 时,请说明 ;(3)、设 的面积为 ,求S与t之间的关系式.
(1)、用含有t的代数式表示 和 的长度;(2)、当 时,请说明 ;(3)、设 的面积为 ,求S与t之间的关系式.