山东省青岛市崂山区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 从 年末开始,一场新型冠状病毒疫情席卷了全世界,面对疫情我国人民在党的领导下团结一心取得了决定性胜利.新冠病毒的直径约为 米,将 用科学记数法表示为( )A、 B、 C、 D、2. 2017年12月15日,北京2022年冬奥会会徽“冬梦”正式发布. 以下是参选的会徽设计的一部分图形,其中是轴对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 3. 计算 得( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 与直线 相交,已知 ,则 的度数为( )
3. 计算 得( )A、 B、 C、 D、4. 下列运算正确的是( )A、 B、 C、 D、5. 如图,直线 与直线 相交,已知 ,则 的度数为( ) A、 B、 C、 D、6. 如图,直线 ,直线l与a,b分别相交于A,B两点,过点A作直线l的垂线交直线b于点C,若 ,则 的度数为( )
A、 B、 C、 D、6. 如图,直线 ,直线l与a,b分别相交于A,B两点,过点A作直线l的垂线交直线b于点C,若 ,则 的度数为( ) A、 B、 C、 D、7. 某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:
A、 B、 C、 D、7. 某品牌热水壶的成本为50元,销售商对其销量与定价的关系进行了调查,结果如下:定价/元
70
80
90
100
110
120
销量/把
80
100
110
100
80
60
现销售了 把水壶,则定价约为( )
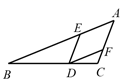
A、 元 B、 元 C、 元 D、 元8. 如图,在 中,已知点 分别是 上的中点,且 的面积为 ,则 的面积为( ) A、 B、 C、 D、 2
A、 B、 C、 D、 2二、填空题
-
9. 如图, ,则 度数为 .
 10. 一个底面是正方形的长方体,高为 ,底面正方形边长为 .如果正方形的边长增加了 ,那么它的体积增加了 .11. 小明家距离学校 千米,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程 与他所用的时间 之间的关系.如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到分钟?(结果精确到 )
10. 一个底面是正方形的长方体,高为 ,底面正方形边长为 .如果正方形的边长增加了 ,那么它的体积增加了 .11. 小明家距离学校 千米,小明骑车上学途中,自行车出现故障,恰好路边有便民服务点,几分钟后车修好了,他增加速度骑车到校.我们根据小明的这段经历画了一幅图象(如图),该图描绘了小明行的路程 与他所用的时间 之间的关系.如果自行车未出现故障,小明一直用修车前的速度行驶,那么他比实际情况早到分钟?(结果精确到 ) 12. 如图在 中, , 平分 ,交 于点D, 垂直平分 ,交 于点E,若 , ,则 .
12. 如图在 中, , 平分 ,交 于点D, 垂直平分 ,交 于点E,若 , ,则 .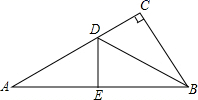 13. 已知 的高为 , , ,则 的度数是 .14. 的个位数为 .
13. 已知 的高为 , , ,则 的度数是 .14. 的个位数为 .三、解答题
-
15. 请用直尺、圆规作图,不写作法,但要保留作图痕迹.
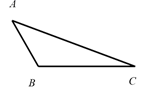
已知:如图 .
求作:一点O,使点O到边 与 距离相等,且点O到点B与点C的距离也相等.
16. 计算题(1)、(2)、17. 求下列各式的值(1)、 ,其中(2)、 ,其中18. 请你设计一个转盘,使得自由转动这个转盘,转盘停止后,指针落在1号区域的概率为 ,落在2号区域的概率为 ,落在3号区域的概率 .19. 梯形的上底长为x,下底长为y,高为 ,面积为 .(1)、梯形下底长y与上底长x之间的关系式是什么?(2)、用表格表示当x从 变到 (每次增加1),y的相应值;(3)、当x每增加 时,y如何变化?20. 已知如图所示 中, , ,请你将 分成两个等腰三角形,并说明分法的合理性. 21. 计算(1)、(2)、22. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏;小明从中任意抽取一张牌(不放回) ,小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.(1)、若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?
21. 计算(1)、(2)、22. 小明和小颖用一副去掉大、小王的扑克牌做摸牌游戏;小明从中任意抽取一张牌(不放回) ,小颖从剩余的牌中任意抽取一张,谁摸到的牌面大谁就获胜(规定牌面从小到大的顺序为:2,3,4,5,6,7,8,9,10,J,Q,K,A,且牌面的大小与花色无关).然后两人把摸到的牌都放回,重新开始游戏.(1)、若小明已经摸到的牌面为4,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(2)、若小明已经摸到的牌面为2,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?(3)、若小明已经摸到的牌面为A,然后小颖摸牌,那么小明获胜的概率是多少?小颖获胜的概率又是多少?
