山东省东营市垦利区2019-2020学年七年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
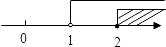
1. 若 是下列某二元一次方程组的解,则这个方程组为( )A、 B、 C、 D、2. 下列语句中,假命题的是( )A、垂线段最短 B、如果直线a、b、c满足a∥b , b∥c , 那么a∥c C、同角的余角相等 D、如果∠AOB=80°,∠BOC=20°,那么∠AOC=60°3. 下列各选项的事件中,发生的可能性大小相等的是( )A、小明去某路口,碰到红灯,黄灯和绿灯 B、掷一枚图钉,落地后钉尖“朝上”和“朝下” C、小亮在沿着Rt△ABC三边行走他出现在AB , AC与BC边上 D、小红掷一枚均匀的骰子,朝上的点数为“偶数”和“奇数”4. 不等式组 的解集在数轴上表示正确的是( )A、
 B、
B、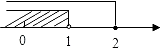 C、
C、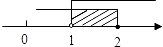 D、
D、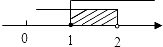 5. 把方程3x﹣5y=2写成用x的代数式表示y的形式是( )A、x=15y+6 B、 C、 D、6. 如图,AB∥ED , CM平分∠BCE , CN⊥CM , ∠B=60°,则∠DCN为( )
5. 把方程3x﹣5y=2写成用x的代数式表示y的形式是( )A、x=15y+6 B、 C、 D、6. 如图,AB∥ED , CM平分∠BCE , CN⊥CM , ∠B=60°,则∠DCN为( )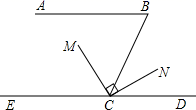 A、30° B、60° C、25° D、35°7. 把一副三角板按如图所示平放在桌面上,点E恰好落在CB的延长线上,FE⊥EC,则∠BDE的大小为( )
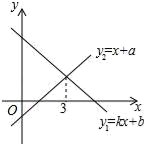
A、30° B、60° C、25° D、35°7. 把一副三角板按如图所示平放在桌面上,点E恰好落在CB的延长线上,FE⊥EC,则∠BDE的大小为( ) A、10° B、15° C、25° D、30°8. 若关于x的一元一次不等式组 无解,则a的取值范围是( )A、a≥6 B、a>6 C、a≤﹣6 D、a<﹣69. 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论中正确的个数是( )
A、10° B、15° C、25° D、30°8. 若关于x的一元一次不等式组 无解,则a的取值范围是( )A、a≥6 B、a>6 C、a≤﹣6 D、a<﹣69. 一次函数y1=kx+b与y2=x+a的图象如图所示,则下列结论中正确的个数是( )①y2随x的增大而减小;②3k+b=3+a;③当x<3时,y1<y2; ④当x>3时,y1<y2 .
 A、3 B、2 C、1 D、010. 如图,△ABC是等边三角形,E、F分别在AC、BC上,且AE=CF , 则下列结论:①AF=BE , ②∠BDF=60°,③∠CAF=∠ABE , ④BD=CE , 其中正确的个数是( )个.
A、3 B、2 C、1 D、010. 如图,△ABC是等边三角形,E、F分别在AC、BC上,且AE=CF , 则下列结论:①AF=BE , ②∠BDF=60°,③∠CAF=∠ABE , ④BD=CE , 其中正确的个数是( )个.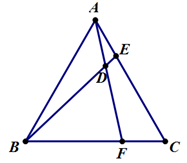 A、1 B、2 C、3 D、4
A、1 B、2 C、3 D、4二、填空题
-
11. 已知2a>b , 则2a﹣0.5b﹣0.5(填“>”或“<”)12. 在一个不透明的盒子中装有 个黑球,n个红球,它们除颜色不同外,其余均相同.若从中随机摸出一个球,它是黑球的概率为 ,则 .13. 如图,给出下列条件:① ;② ;③ ;④ ;⑤ .其中,一定能判定 ∥ 的条件有(填写所有正确的序号).
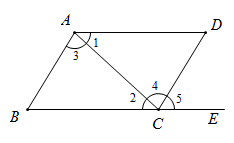 14. 如图,直线 ,以直线 上的点A为圆心,适当长为半径在右侧画弧,分别交 , 于点 .连结 , .若 ,则 的度数是 .
14. 如图,直线 ,以直线 上的点A为圆心,适当长为半径在右侧画弧,分别交 , 于点 .连结 , .若 ,则 的度数是 .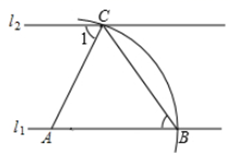 15. 如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是cm.
15. 如图,在△ABC中,DE是AB的垂直平分线,交BC于点D,交AB于点E,已知AE=1cm,△ACD的周长为12cm,则△ABC的周长是cm. 16. 一次新冠病毒防疫知识竞赛有25道题,评委会决定:答对一道题得4分,答错或不答一题扣1分,在这次知识竞赛中,小明被评为优秀(85分或85分以上),那么小明至少答对了道题.17. 如果关于x、y的方程组 的解满足x-2y=-1,则k =.18. 如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,从左起第1个等边三角形的边长记为 ,第2个等边三角形的边长记为 ,以此类推.若 ,则 .
16. 一次新冠病毒防疫知识竞赛有25道题,评委会决定:答对一道题得4分,答错或不答一题扣1分,在这次知识竞赛中,小明被评为优秀(85分或85分以上),那么小明至少答对了道题.17. 如果关于x、y的方程组 的解满足x-2y=-1,则k =.18. 如图, ,点 、 、 …在射线 上,点 、 、 …在射线 上, 、 、 …均为等边三角形,从左起第1个等边三角形的边长记为 ,第2个等边三角形的边长记为 ,以此类推.若 ,则 .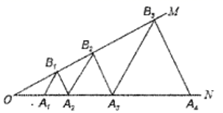
三、解答题
-
19. 计算:(1)、解方程组:(2)、解不等式:2(x+1)﹣1≥3x+2,并把它的解集表示在数轴上;(3)、解不等式组: ,并写出它的所有非负整数解.20. 如图是潜望镜工作原理示意图,阴影部分是平行放置在潜望镜里的两面镜子.已知光线经过镜子反射时,有∠1=∠2,∠3=∠4,请解释进入潜望镜的光线 为什么和离开潜望镜的光线m是平行的?
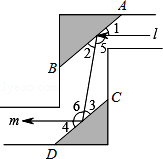
理由:
21. 如图,△ABC和△ADE都是等边三角形,点B在ED的延长线上. (1)、求证:△ABD≌△ACE;(2)、若AE=2,CE=3,求BE的长;(3)、求∠BEC的度数22. 新冠疫情以来,各地政府为活跃消费市场,释放消费潜力,各商家采取各种促销以此来对冲疫情影响.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券(若指向边界则重转),凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)、求证:△ABD≌△ACE;(2)、若AE=2,CE=3,求BE的长;(3)、求∠BEC的度数22. 新冠疫情以来,各地政府为活跃消费市场,释放消费潜力,各商家采取各种促销以此来对冲疫情影响.某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券(若指向边界则重转),凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.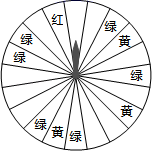 (1)、求转动一次转盘获得购物券的概率;(2)、某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.23. 如图,直线 的函数表达式为 ,且直线 与x轴交于点D.直线 与x轴交于点A,且经过点B(4,1),直线 与 交于点 .
(1)、求转动一次转盘获得购物券的概率;(2)、某顾客在此商场购物220元,通过转转盘获得购物券和直接获得购物券,你认为哪种方式对顾客更合算?谈谈你的理由.23. 如图,直线 的函数表达式为 ,且直线 与x轴交于点D.直线 与x轴交于点A,且经过点B(4,1),直线 与 交于点 .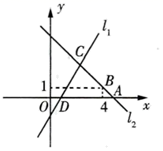 (1)、求点D和点C的坐标;(2)、求直线 的函数表达式;(3)、利用函数图象写出关于x,y的二元一次方程组 的解.24. 阅读下列文字,请仔细体会其中的数学思想.(1)、解方程组 ,我们利用加减消元法,很快可以求得此方程组的解为;(2)、如何解方程组 呢?我们可以把m+5,n+3看成一个整体,设m+5=x , n+3=y , 很快可以求出原方程组的解为;(3)、由此请你解决下列问题:
(1)、求点D和点C的坐标;(2)、求直线 的函数表达式;(3)、利用函数图象写出关于x,y的二元一次方程组 的解.24. 阅读下列文字,请仔细体会其中的数学思想.(1)、解方程组 ,我们利用加减消元法,很快可以求得此方程组的解为;(2)、如何解方程组 呢?我们可以把m+5,n+3看成一个整体,设m+5=x , n+3=y , 很快可以求出原方程组的解为;(3)、由此请你解决下列问题:若关于m , n的方程组 与 有相同的解,求a、b的值.
25. 列方程组(或不等式组)解应用题:垦利区为打好创城攻坚战,在城市创卫工作中 “保护好环境,拒绝冒黑烟”,公交公司将淘汰某一条线路上“冒黑烟”较严重的公交车,计划购买A型和B型两种环保节能公交车共10辆.若购买A型公交车3辆,B型公交车2辆,共需180万元;若购买A型公交车2辆,B型公交车3辆,共需195万元.
(1)、求购买A型和B型公交车每辆各需多少万元;(2)、预计在该线路上A型和B型公交车每辆年均载客量分别为60万人次和100万人次,若该公司购买A型和B型公交车的总费用不超过360万元,且确保这10辆公交车在该线路的年均载客总和不少于680万人次,则该公司有哪几种购车方案,哪种购车方案总费用最少?最少总费用是多少?