云南省怒江傈僳族自治州兰坪白族普米族自治县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、填空题
-
1. 计算 的结果是.2. 在平行四边形ABCD中,若 与 的度数之比为 ,则 的度数为 .3. 直线y=3x向下平移3个单位长度得到的直线是4. 一组数据30,18,24,26,33,28的中位数是.5. 如果一个正多边形的每个外角都等于72°,那么它是正边形。6. 因式分解:a2+ab﹣a= .
二、单选题
-
7. 下列图形中,轴对称图形有( )



 A、1个 B、2个 C、3个 D、4个8. 下列四组线段中,能组成直角三角形的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,69. 如图,两个正方形的面积分别是100和36,则字母B所代表的正方形的面积是( )
A、1个 B、2个 C、3个 D、4个8. 下列四组线段中,能组成直角三角形的是( )A、1,2,3 B、2,3,4 C、3,4,5 D、4,5,69. 如图,两个正方形的面积分别是100和36,则字母B所代表的正方形的面积是( ) A、8 B、10 C、64 D、13610. 要使二次根式 有意义,则x的取值可以是( )A、0 B、1 C、2 D、411. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )
A、8 B、10 C、64 D、13610. 要使二次根式 有意义,则x的取值可以是( )A、0 B、1 C、2 D、411. 如图,▱ABCD的对角线AC、BD相交于点O , 且AC+BD=24.若△OAB的周长是20,则AB的长为( )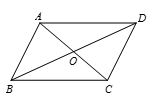 A、8 B、9 C、10 D、1212. 一组数据4,10,12,14,则这组数据的平均数是A、9 B、10 C、11 D、1213. 下列四个命题中错误的是( )A、对角线相等的菱形是正方形 B、有两边相等的平行四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分的四边形是平行四边形14. 一次函数 与 交于点 ,则方程组 的解是( )A、 B、 C、 D、
A、8 B、9 C、10 D、1212. 一组数据4,10,12,14,则这组数据的平均数是A、9 B、10 C、11 D、1213. 下列四个命题中错误的是( )A、对角线相等的菱形是正方形 B、有两边相等的平行四边形是菱形 C、对角线相等的平行四边形是矩形 D、对角线互相平分的四边形是平行四边形14. 一次函数 与 交于点 ,则方程组 的解是( )A、 B、 C、 D、三、解答题
-
15. 计算: .16. 如图,DC⊥CA,EA⊥CA,CD=AB,CB=AE.求证:△BCD≌△EAB.
 17. 如图,一棵小树在大风中被吹歪,用一根棍子把小树扶直,已知支撑点到地面的距离是 米,棍子的长度为5.5米,求棍子和地面接触点 到小树底部 的距离是多少?
17. 如图,一棵小树在大风中被吹歪,用一根棍子把小树扶直,已知支撑点到地面的距离是 米,棍子的长度为5.5米,求棍子和地面接触点 到小树底部 的距离是多少?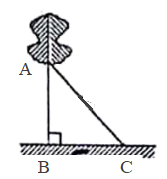 18. 如图,在 中, , 是 边上的中线,过点B作 ,过点C作 , , 相交于点E.
18. 如图,在 中, , 是 边上的中线,过点B作 ,过点C作 , , 相交于点E.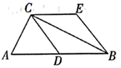
求证:四边形 是菱形.
19. 一次函数 的图像经过 , 两点.(1)、求 的值;(2)、判断点 是否在该函数的图象上.20. 如图, 是等腰三角形,D为底边 的中点,若 且等于 的一半,求证:四边形 是矩形. 21. 校运会期间,某班预计用90元为班级同学统一购买矿泉水,生活委员发现学校小卖部有优惠活动:购买瓶装矿泉水打9折,经计算按优惠价购买能多买10瓶,求每瓶矿泉水的原价和该班实际购买矿泉水的数量.22. 某公司要招聘一名员工,10名应聘者的成绩(单位:分)如下:
21. 校运会期间,某班预计用90元为班级同学统一购买矿泉水,生活委员发现学校小卖部有优惠活动:购买瓶装矿泉水打9折,经计算按优惠价购买能多买10瓶,求每瓶矿泉水的原价和该班实际购买矿泉水的数量.22. 某公司要招聘一名员工,10名应聘者的成绩(单位:分)如下:编号
1
2
3
4
5
6
7
8
9
10
技能测试
90
82
70
80
92
85
80
75
95
80
计算机
80
90
89
70
90
90
80
80
90
90
(1)、求出这10名应聘者的技能测试成绩的中位数和众数;(2)、公司抽取了编号为1,5,9,技能测试成绩为前三名应聘者计算总成绩,若技能测试成绩和计算机成绩按4:6的比例进行计算,求被录取的应聘者的编号.23. 如图,平行四边形 的顶点A的坐标为 , ,点M的坐标为 ,直线l过M,C两点.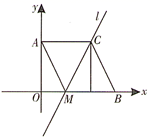 (1)、直接写出点B,C的坐标;(2)、求直线l的函数解析式;(3)、在直线l上是否存在一点P,使得以点P,A,C为顶点的三角形的面积为4?若存在,求出点P的坐标;若不存在,请说明理由.
(1)、直接写出点B,C的坐标;(2)、求直线l的函数解析式;(3)、在直线l上是否存在一点P,使得以点P,A,C为顶点的三角形的面积为4?若存在,求出点P的坐标;若不存在,请说明理由.