云南省昆明市盘龙区禄劝县2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、填空题

1. 计算： $\sqrt{{(- 2)}^{2}}$ ＝．

查看试题解析
2. 2022年将在北京——张家口举办冬季奥运会，北京将成为世界上第一个既举办夏季奥运会，又举办冬季奥运会的城市.某队要从两名选手中选取一名参加比赛，为此对这两名队员进行了五次测试，测试成绩如图所示，选手的成绩更稳定.

查看试题解析
3. 已知 $P_{1} (1, y_{1})$ ， $P_{2} (2, y_{2})$ 在正比例函数 $y = - \frac{1}{4} x$ 的图象上，则 $y_{1}$ $y_{2}$ .（填“ $>$ ”或“ $<$ ”或“ $=$ ”）.

查看试题解析
4. 如图，在菱形 $A B C D$ 中， $A C$ 、 $B D$ 相交于点O， $∠ B A D = 60 °$ ， $B D$ 长为4，则菱形 $A B C D$ 的面积是.

查看试题解析
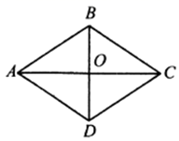5. 小明学了在数轴上表示无理数的方法后，进行了练习：首先画数轴，原点为 $O$ ，在数轴上找到表示数2的点 $A$ ，然后过点 $A$ 作 $A B ⊥ O A$ ，使 $A B = 3$ （如图）；再以 $O$ 为圆心， $O B$ 的长为半径作弧，交数轴正半轴于点 $P$ ，则点 $P$ 所表示的数是.

查看试题解析
6. 如图，在长方形纸片 $A B C D$ 中， $A B = 6 c m$ ， $B C = 8 c m$ ，点 $E$ 是 $B C$ 边上一点，连接 $A E$ 并将 $Δ A E B$ 沿 $A E$ 折叠，得到 $Δ A E B^{'}$ ，以C，E， $B^{'}$ 为顶点的三角形是直角三角形时， $B E$ 的长为 $c m$ .

查看试题解析

二、单选题

7. 若函数 $y = \frac{\sqrt{x - 3}}{4}$ 有意义，则自变量x的取值范围是（）

A、 $x \geq 3$ B、 $x \leq 3$ C、 $x > 3$ D、 $x < 3$

查看试题解析
8. 下列计算正确的是（）

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $3 \sqrt{5} - \sqrt{5} = 3$ C、 $5 \times \sqrt{\frac{1}{5}} = 1$ D、 $\sqrt{12} \div \sqrt{3} = 2$

查看试题解析
9. 在战“疫”诗歌创作大赛中，有7名同学进入了决赛，他们的最终成绩均不同.小弘同学想知道自己能否进入前3名，除要了解自己的成绩外，还要了解这7名同学成绩的（）

A、中位数 B、平均数 C、众数 D、方差

查看试题解析
10. 如图，DE是△ABC的中位线，点F在DE上，且∠AFC=90°，若AC=10，BC=16，则DF的长为（）

A、5 B、3 C、8 D、10

查看试题解析
11. 已知一次函数 $y = a x + b$ （a、b是常数），x与y的部分对应值如下表：

$x$

$- 3$

$- 2$

$- 1$

0

1

2

3

$y$

$- 4$

$- 2$

0

2

4

6

8

下列说法中，错误的是（）

A、图象经过第一、二、三象限 B、函数值y随自变量x的增大而减小 C、方程 $a x + b = 0$ 的解是 $x = - 1$ D、不等式 $a x + b > 0$ 的解集是 $x > - 1$

查看试题解析
12. 关于▱ABCD的叙述，正确的是（）

A、若AB⊥BC，则▱ABCD是菱形 B、若AC⊥BD，则▱ABCD是正方形 C、若AC=BD，则▱ABCD是矩形 D、若AB=AD，则▱ABCD是正方形

查看试题解析
13. 如图，小巷左右两侧是竖直的墙，一架梯子斜靠在左墙时，梯子底端到左墙角的距离 $B C$ 为0.7米，梯子顶端到地面的距离 $A C$ 为2.4米，如果保持梯子底端位置不动，将梯子斜靠在右墙时，梯子顶端到地面的距离 $A^{'} D$ 为1.5米，则小巷的宽为（）

A、2.5米 B、2.6米 C、2.7米 D、2.8米

查看试题解析
14. 如图，在平行四边形ABCD中，∠DBC=45°，DE⊥BC于E，BF⊥CD于F，DE，BF相交于H，BF与AD的延长线相交于点G，下面给出四个结论：① $B D = \sqrt{2} B E$ ； ②∠A=∠BHE； ③AB=BH； ④△BCF≌△DCE，其中正确的结论是（）.

A、①②③ B、①②④ C、②③④ D、①②③④

查看试题解析

三、解答题

15. 计算：

(1)、 $\sqrt{27} - \sqrt{8} \times \sqrt{6} + 3 \sqrt{\frac{1}{3}}$

(2)、 $\frac{\sqrt{12} \times \sqrt{6}}{\sqrt{18}} - {(\sqrt{3} - \sqrt{2})}^{2}$

查看试题解析
16. 如图，平行四边形 $A B C D$ 的对角线 $A C$ 、 $B D$ 相交于点O，E、F是 $A C$ 上的两点，且 $B F / / D E$ .

(1)、求证： $Δ B F O ≌ Δ D E O$ ；

(2)、求证：四边形 $B F D E$ 是平行四边形.

查看试题解析
17. 如图：已知直线 $y = k x + b$ 经过点 $A (5 ， 0)$ ， $B (1 ， 4)$ ．

(1)、求直线 $A B$ 的解析式；

(2)、若直线 $y = 2 x - 4$ 与直线 $A B$ 相交于点C，求点C的坐标；

(3)、根据图象，直接写出关于x的不等式 $2 x - 4 > k x + b > 0$ 的解集．

查看试题解析
18. 如图，在 $△ A B C$ 中， $∠ A D C = 90 °$ ，若 $C D = 12$ ， $A D = 16$ ， $B C = 15$ .

(1)、求 $A C$ ， $B D$ 的长.

(2)、判断 $△ A B C$ 的形状并说明理由.

查看试题解析
19. 某校招聘一名数学老师，对应聘者分别进行了教学能力、科研能力和组织能力三项测试，其中甲、乙两名应聘者的成绩如右表：（单位：分）

教学能力

科研能力

组织能力

甲

81

85

86

乙

92

80

74

(1)、若根据三项测试的平均成绩在甲、乙两人中录用一人，那么谁将被录用；

(2)、根据实际需要，学校将教学、科研和组织能力三项测试得分按 5：3：2 的比确定每人的最后成绩，若按此成绩在甲、乙两人中录用一人，谁将被录用？

查看试题解析
20. 观察、发现：
$\frac{1}{\sqrt{2} + 1} = \frac{\sqrt{2} - 1}{(\sqrt{2} + 1) (\sqrt{2} - 1)} = \frac{\sqrt{2} - 1}{{(\sqrt{2})}^{2} - 1} = \frac{\sqrt{2} - 1}{2 - 1} = \sqrt{2} - 1$

$\frac{1}{\sqrt{3} + \sqrt{2}} = \frac{\sqrt{3} - \sqrt{2}}{(\sqrt{3} + \sqrt{2}) (\sqrt{3} - \sqrt{2})} = \frac{\sqrt{3} - \sqrt{2}}{{(\sqrt{3})}^{2} - {(\sqrt{2})}^{2}} = \frac{\sqrt{3} - \sqrt{2}}{3 - 2} = \sqrt{3} - \sqrt{2}$

……

(1)、试化简： $\frac{1}{\sqrt{11} + \sqrt{10}}$

(2)、直接写出： $\frac{1}{\sqrt{n + 1} + \sqrt{n}} =$ ；

(3)、求值： $\frac{1}{\sqrt{2} + 1} + \frac{1}{\sqrt{3} + \sqrt{2}} + \frac{1}{\sqrt{4} + \sqrt{3}} + \dots + \frac{1}{\sqrt{100} + \sqrt{99}}$

查看试题解析
21. 如图，在△ABC中，AB=AC，AD ⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE ⊥AN，垂足为点E．

(1)、求证：四边形ADCE为矩形；

(2)、当△ABC满足什么条件时，四边形ADCE是一个正方形?并给出证明．

查看试题解析
22. 某商店销售A型和B型两种型号的电脑，销售一台A型电脑可获利120元，销售一台B型电脑可获利140元．该商店计划一次购进两种型号的电脑共100台，其中B型电脑的进货量不超过A型电脑的3倍．设购进A型电脑x台，这100台电脑的销售总利润为y元．

(1)、求y与x的关系式；

(2)、该商店购进A型、B型电脑各多少台，才能使销售利润最大？最大利润是多少？

(3)、若限定商店最多购进A型电脑60台，则这100台电脑的销售总利润能否为12760元？请说明理由．

查看试题解析
23. 问题情境：如图，在平面直角坐标系中，点O是坐标原点，四边形 $A B C O$ 是菱形，点A的坐标为 $(a ， b)$ ，且a和b满足 $a = \sqrt{b - 4} + \sqrt{4 - b} - 3$ ；点C在x轴的正半轴上，直线 $A C$ 交y轴于点M， $A B$ 边交y轴于点H，连接 $B M$ ；

(1)、求点A的坐标和菱形 $A B C O$ 的边长；

(2)、求直线 $A C$ 的解析式；

(3)、问题探究：
动点P从点A出发，沿折线 $A B C$ 方向以2个单位长度/秒的速度向终点C匀速运动，设 $Δ P M B$ 的面积为 $S (S \neq 0)$ ，点P的运动时间为t秒，

①求S与t之间的函数关系式；

②在点P运动过程中，当 $S = 3$ 时，请求出t的值.

查看试题解析

$x$	$- 3$	$- 2$	$- 1$	0	1	2	3
$y$	$- 4$	$- 2$	0	2	4	6	8

	教学能力	科研能力	组织能力
甲	81	85	86
乙	92	80	74