山东省烟台蓬莱市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 若方程 是关于x,y的二元一次方程,则a的值为( )A、-3 B、±2 C、±3 D、32. 下列不等式变形,不成立的是( )A、若 ,则 B、若 ,则 C、若 ,则 D、若 ,则3. 不等式组 的解集在数轴上表示正确的是( )A、
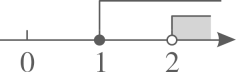 B、
B、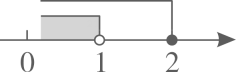 C、
C、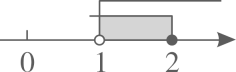 D、
D、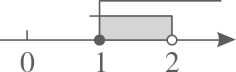 4. 不等式 的解集是 那么( )A、 B、 C、 D、5. 如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,若向正方形网格中投针,落在△ABC内部的概率是( )
4. 不等式 的解集是 那么( )A、 B、 C、 D、5. 如图,在边长为1的小正方形网格中,△ABC的三个顶点均在格点上,若向正方形网格中投针,落在△ABC内部的概率是( ) A、 B、 C、 D、6. 关于x的不等式组 的解集为 ,那么a的取值范围为( )A、 B、 C、 D、7. 关于 的二元一次方程组 的解满足 ,则a的值为( )A、 B、 C、 D、8. 已知关于 的二元一次方程组 满足 ,则k的取值范围( )A、 B、 C、 D、以上答案都不对9. 如图,在长方形 中, ,将长方形 沿E折叠,点A落在 处,若 的延长线恰好过点 则 的长为( )
A、 B、 C、 D、6. 关于x的不等式组 的解集为 ,那么a的取值范围为( )A、 B、 C、 D、7. 关于 的二元一次方程组 的解满足 ,则a的值为( )A、 B、 C、 D、8. 已知关于 的二元一次方程组 满足 ,则k的取值范围( )A、 B、 C、 D、以上答案都不对9. 如图,在长方形 中, ,将长方形 沿E折叠,点A落在 处,若 的延长线恰好过点 则 的长为( ) A、 B、 C、 D、10. 如图,已知P到 三边距离相等, ,则 的周长为( )
A、 B、 C、 D、10. 如图,已知P到 三边距离相等, ,则 的周长为( ) A、 B、 C、 D、11. 如果不等式3x-m≤0的正整数解是1,2,3,那么m的取值范围是( )A、m>9 B、m 12 C、 D、12. 如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC边上的动点,连接DM 、ME、CM、DE, DE与CM相交于点F且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM是等腰三角形; (3)∠CDM=∠CFE;(4)AD2+BE2=DE2;(5)四边形CDME的面积发生改变.其中正确的结论有( )个.
A、 B、 C、 D、11. 如果不等式3x-m≤0的正整数解是1,2,3,那么m的取值范围是( )A、m>9 B、m 12 C、 D、12. 如图,在△ABC中,AC=BC,∠ACB=90°,M是AB边上的中点,点D、E分别是AC、BC边上的动点,连接DM 、ME、CM、DE, DE与CM相交于点F且∠DME=90°.则下列5个结论: (1)图中共有两对全等三角形;(2)△DEM是等腰三角形; (3)∠CDM=∠CFE;(4)AD2+BE2=DE2;(5)四边形CDME的面积发生改变.其中正确的结论有( )个. A、2 B、3 C、4 D、5
A、2 B、3 C、4 D、5二、填空题
-
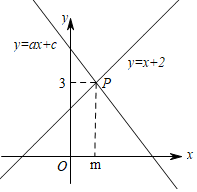
13. 已知不等式组 的解集为 ,则 的值是.14. 如图,直线y=x+2与直线y=ax+c相交于点P(m , 3),则关于x的不等式x+2≤ax+c的解为 .
 15. 已知关于 的二元一次方程组 的解为 ,若 满足二元一次方程组 ,则 .16. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是.
15. 已知关于 的二元一次方程组 的解为 ,若 满足二元一次方程组 ,则 .16. 如图,在Rt△ABC中,∠ACB=90°,AB的垂直平分线DE交AC于E,交BC的延长线于F,若∠F=30°,DE=1,则BE的长是. 17. 已知:如图,在长方形 中, , .延长 到点E,使 ,连接 ,动点P从点B出发,以每秒2个单位的速度沿 向终点A运动,设点P的运动时间为t秒,当t的值为秒时, 和 全等.
17. 已知:如图,在长方形 中, , .延长 到点E,使 ,连接 ,动点P从点B出发,以每秒2个单位的速度沿 向终点A运动,设点P的运动时间为t秒,当t的值为秒时, 和 全等. 18. 如图,在四边形 中, , 交 于点E,交 于点F, , ,则 .
18. 如图,在四边形 中, , 交 于点E,交 于点F, , ,则 .
三、解答题
-
19. 方程组 与 有相同的解,求 的值.20.(1)、解不等式 ,并在数轴上表示解集.
 (2)、解不等式组: ,并写出该不等式组的整数解.(3)、解不等式组:21. 是否存在这样的整数m,使得关于x,y的方程组 的解满足x<0且y>0?若存在,求出整数m;若不存在,请说明理由。22. 如图,已知 为 的平分线, 于 ,求 的度数.
(2)、解不等式组: ,并写出该不等式组的整数解.(3)、解不等式组:21. 是否存在这样的整数m,使得关于x,y的方程组 的解满足x<0且y>0?若存在,求出整数m;若不存在,请说明理由。22. 如图,已知 为 的平分线, 于 ,求 的度数. 23. 如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.
23. 如图,在△ABC中,BC边上的垂直平分线DE与∠BAC的平分线交于点E,EF⊥AB交AB的延长线于点F,EG⊥AC于点G.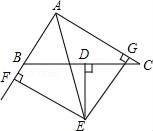
求证:
(1)、BF=CG;(2)、AB+AC=2AF.24. 某蔬菜种植基地为提高蔬菜产量,计划对甲、乙两种型号蔬菜大棚进行改造,根据预算,改造2个甲种型号大棚比1个乙种型号大棚多需资金6万元,改造1个甲种型号大棚和2个乙种型号大棚共需资金48万元.(1)、改造1个甲种型号和1个乙种型号大棚所需资金分别是多少万元?(2)、已知改造1个甲种型号大棚的时间是5天,改造1个乙种型号大概的时间是3天,该基地计划改造甲、乙两种蔬菜大棚共8个,改造资金最多能投入128万元,要求改造时间不超过35天,请问有几种改造方案?哪种方案基地投入资金最少,最少是多少?25. 问题探究:如图1,在 中,点D是 的中点, 交 于点 交 于 ,连接 . (1)、 与 之间的关系为: ;(填“ ”、“ ”或“ ”)(2)、若 ,探索线段 之间的等量关系,并加以证明.(3)、问题解决:如图2.在四边形 中, 以D为顶点作 的两边分别交 于 两点,连接 ,探索线段 之间的数量关系,并加以证明.
(1)、 与 之间的关系为: ;(填“ ”、“ ”或“ ”)(2)、若 ,探索线段 之间的等量关系,并加以证明.(3)、问题解决:如图2.在四边形 中, 以D为顶点作 的两边分别交 于 两点,连接 ,探索线段 之间的数量关系,并加以证明.