山东省泰安市肥城市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列说法:①所有无理数都能用数轴上的点表示;②带根号的数都是无理数;③任何实数都有立方根;④ 的平方根是±4,其中正确的个数有( )A、0个 B、1个 C、2个 D、3个2. 下列美丽的图案中,既是轴对称图形又是中心对称图形的个数是( )
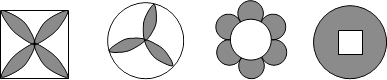 A、1个 B、2个 C、3个 D、4个3. 在二次根式 , , , , , , 中,最简二次根式的个数为( )A、1个 B、2个 C、3个 D、4个4. 关于 的不等式组 恰好只有四个整数解,则 的取值范围是( )A、 B、 C、 D、5.
A、1个 B、2个 C、3个 D、4个3. 在二次根式 , , , , , , 中,最简二次根式的个数为( )A、1个 B、2个 C、3个 D、4个4. 关于 的不等式组 恰好只有四个整数解,则 的取值范围是( )A、 B、 C、 D、5.如图,正方形ABCD的边长为2cm,动点P从点A出发,在正方形的边上沿A→B→C的方向运动到点C停止,设点P的运动路程为x(cm),在下列图象中,能表示△ADP的面积y(cm2)关于x(cm)的函数关系的图象是( )
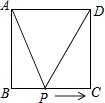 A、
A、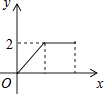 B、
B、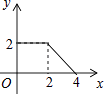 C、
C、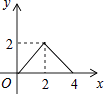 D、
D、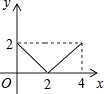 6. 如果一次函数y=mx+n的图象经过第一、二、四象限,则一次函数y=nx+m不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 定义运算“※”为a※b= ,如1※(﹣2)=1×(﹣2)=﹣2,则函数y=2※x的图象大致是( )A、
6. 如果一次函数y=mx+n的图象经过第一、二、四象限,则一次函数y=nx+m不经过的象限是( )A、第一象限 B、第二象限 C、第三象限 D、第四象限7. 定义运算“※”为a※b= ,如1※(﹣2)=1×(﹣2)=﹣2,则函数y=2※x的图象大致是( )A、 B、
B、 C、
C、 D、
D、 8. 下列说法中,错误的是( )A、有一条对角线平分一个内角的平行四边形是菱形 B、对角线互相垂直且平分的四边形是菱形 C、一条对角线平分另一条对角线的四边形是平行四边形 D、三角形的一条中位线与第三边上的中线互相平分9. 如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB、AC、BD的中点,若BC=6,则 的周长是( )
8. 下列说法中,错误的是( )A、有一条对角线平分一个内角的平行四边形是菱形 B、对角线互相垂直且平分的四边形是菱形 C、一条对角线平分另一条对角线的四边形是平行四边形 D、三角形的一条中位线与第三边上的中线互相平分9. 如图,在四边形ABCD中,AD=BC,∠DAB=50°,∠CBA=70°,P、M、N分别是AB、AC、BD的中点,若BC=6,则 的周长是( ) A、6 B、9 C、12 D、1810. 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( )
A、6 B、9 C、12 D、1810. 如图,在正方形网格中,线段A′B′是线段AB绕某点逆时针旋转角α得到的,点A′与A对应,则角α的大小为( ) A、30° B、60° C、90° D、120°11. 如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( )
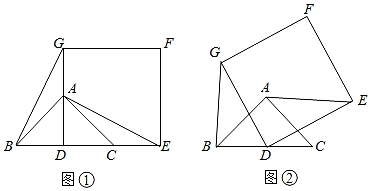
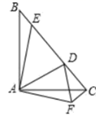
A、30° B、60° C、90° D、120°11. 如图,菱形纸片ABCD,∠A=60°,P为AB中点,折叠菱形纸片ABCD,使点C落在DP所在的直线上,得到经过点D的折痕DE,则∠DEC等于( ) A、60° B、65° C、75° D、80°12. 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的.
A、60° B、65° C、75° D、80°12. 如图,在Rt△ABC中,AB=AC,D,E是斜边BC上两点,且∠DAE=45°,将△ABE绕点A顺时针旋转90°后,得到△ACF,连接DF,则下列结论中有( )个是正确的.①∠DAF=45° ②△ABE≌△ACD ③AD平分∠EDF ④
 A、4 B、3 C、2 D、1
A、4 B、3 C、2 D、1二、填空题
-
13. 已知关于x的不等式 的解集如图所示则a的值为 .
 14. 如图,正方形ABCD的对角线相交于点O,对角线长为1cm,过点O任作一条直线分别交AD,BC于E,F,则阴影部分的面积是 .
14. 如图,正方形ABCD的对角线相交于点O,对角线长为1cm,过点O任作一条直线分别交AD,BC于E,F,则阴影部分的面积是 . 15. 在直角坐标系中,已知点A(1,5),B(3,1),点M在x轴上,则AM+BM的最小值为 .16. 等式 成立的条件是.17. 如图,矩形ABCD中,AB=6,BC=8,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是 .
15. 在直角坐标系中,已知点A(1,5),B(3,1),点M在x轴上,则AM+BM的最小值为 .16. 等式 成立的条件是.17. 如图,矩形ABCD中,AB=6,BC=8,E为AD中点,F为AB上一点,将△AEF沿EF折叠后,点A恰好落到CF上的点G处,则折痕EF的长是 . 18. 如图,在平面直角坐标系中,△P1OA1 , △P2A1A2 , △P3A2A3 , …都是等腰直角三角形,其直角顶点P1(3,3),P2 , P3 , …均在直线 上.设△P1OA1 , △P2A1A2 , △P3A2A3 , …的面积分别为 S1 , S2 , S3 , …,依据图形所反映的规律,S2020=.
18. 如图,在平面直角坐标系中,△P1OA1 , △P2A1A2 , △P3A2A3 , …都是等腰直角三角形,其直角顶点P1(3,3),P2 , P3 , …均在直线 上.设△P1OA1 , △P2A1A2 , △P3A2A3 , …的面积分别为 S1 , S2 , S3 , …,依据图形所反映的规律,S2020=.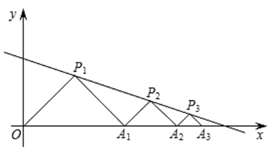
三、解答题
-
19. 解不等式组,并将其解集在数轴表示出来.
.
20. 计算:(1)、 ;(2)、 .21. 如图,在平面直角坐标系xOy中,A(﹣1,5),B(﹣1,0),C(﹣4,3).
(1)作出△ABC向下平移1个单位,再向左平移2个单位后的图形△A1B1C1 .
(2)作出△ABC以A为旋转中心逆时针旋转90°后的图形△A2B2C2 .
(3)求出四边形ACBC2的周长和面积
22. 在平面直角坐标系中,直线l1:y1=k1x+b1与x轴交于点B(12,0),与直线l2:y2=k2x交于点A (6,3). (1)、分别求出直线l1和直线l2的表达式;(2)、直接写出不等式k1x+b1<k2x的解集;(3)、若点D是直线l2上一点,且S△COD= S△AOC , 试求点D的坐标.23. 在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点,PF⊥BD于点F,PA=PF.
(1)、分别求出直线l1和直线l2的表达式;(2)、直接写出不等式k1x+b1<k2x的解集;(3)、若点D是直线l2上一点,且S△COD= S△AOC , 试求点D的坐标.23. 在矩形ABCD中,AE⊥BD于点E,点P是边AD上一点,PF⊥BD于点F,PA=PF. (1)、试判断四边形AGFP的形状,并说明理由.(2)、若AB=1,BC=2,求四边形AGFP的周长.24. 某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:
(1)、试判断四边形AGFP的形状,并说明理由.(2)、若AB=1,BC=2,求四边形AGFP的周长.24. 某家具商场计划购进某种餐桌、餐椅进行销售,有关信息如表:原进价(元/张)
零售价(元/张)
成套售价(元/套)
餐桌
a
270
500元
餐椅
a-110
70
已知用600元购进的餐桌数量与用160元购进的餐椅数量相同.
(1)、求表中a的值;(2)、若该商场购进餐椅的数量是餐桌数量的5倍还多20张,且餐桌和餐椅的总数量不超过200张.该商场计划将一半的餐桌成套(一张餐桌和四张餐椅配成一套)销售,其余餐桌、餐椅以零售方式销售.请问怎样进货,才能获得最大利润?最大利润是多少?(3)、由于原材料价格上涨,每张餐桌和餐椅的进价都上涨了10元,按照(2)中获得最大利润的方案购进餐桌和餐椅,在调整成套销售量而不改变销售价格的情况下,实际全部售出后,所得利润比(2)中的最大利润少了2250元.请问本次成套的销售量为多少?