山东省临沂市罗庄区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 若平行四边形中两个内角的度数比为1：5 ，则其中较大的角是（）

A、60° B、120° C、135° D、150°

查看试题解析
2. $\sqrt{48}$ =（）

A、 $2 \sqrt{12}$ B、 $4 \sqrt{3}$ C、 $2 \sqrt{24}$ D、 $6 \sqrt{8}$

查看试题解析
3. 三角形各边长度的如下，其中不是直角三角形的是（）

A、3，4，5 B、6，8，10 C、5，11，12 D、15，8，17

查看试题解析
4. 如图，从一个大正方形中裁去面积为 $16 c m^{2}$ 和 $24 c m^{2}$ 的两个小正方形，则余下部分的面积为（）

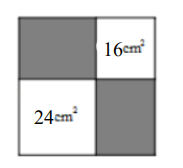A、 $16 \sqrt{6} c m^{2}$ B、 $40 c m^{2}$ C、 $8 \sqrt{6} c m^{2}$ D、 $(2 \sqrt{6} + 4) c m^{2}$

查看试题解析
5. 如图，架在消防车上的云梯AB长为10m，∠ADB=90°，AD=2BD，云梯底部离地面的距离BC为2m，则云梯的顶端离地面的距离AE为（）

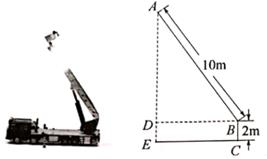A、(2 $\sqrt{5}$ +2)m B、(4 $\sqrt{5}$ +2)m C、(5 $\sqrt{3}$ +2)m D、7m

查看试题解析
6. 某篮球队5名场上队员的身高（单位：cm）是：183，185，188，190，194．现用一名身高为190cm的队员换下场上身高为185cm的队员，与换人前相比，场上队员身高的（）

A、平均数变小，方差变小 B、平均数变小，方差变大 C、平均数变大，方差变小 D、平均数变大，方差变大

查看试题解析
7. 在平面直角坐标系中，若直线y=kx+b经过第一，三，四象限，则直线y=bx+k不经过的象限是（　　）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
8. 今年“五一”节，小明外出爬山，他从山脚爬到山顶的过程中，中途休息了一段时间．设他从山脚出发后所用的时间为t（分钟），所走的路程为s（米），s与t之间的函数关系如图所示，下列说法错误的是（）

A、小明中途休息用了20分钟 B、小明休息前爬山的平均速度为每分钟70米 C、小明在上述过程中所走的路程为6600米 D、小明休息前爬山的平均速度大于休息后爬山的平均速度

查看试题解析
9. 直线y=2x+2沿y轴向下平移6个单位后与x轴的交点坐标是（）

A、（-4，0） B、（-1，0） C、（0，2） D、（2，0）

查看试题解析
10. 如图，在平面直角坐标系中， $▱ A B C D$ 的顶点坐标分别为 $A (3 ， a)$ ， $B (2 ， 2)$ ， $C (b ， 3)$ ， $D (8 ， 6)$ ，则a+b=的值为(　　)

A、8 B、9 C、12 D、11

查看试题解析
11. 如图，小正方形边长为1，连接小正方形的三个顶点得 $Δ ABC$ ，则 $AC$ 边上的高是（）

A、 $\frac{3}{10} \sqrt{5}$ B、 $\frac{3}{2} \sqrt{2}$ C、 $\frac{4}{5} \sqrt{5}$ D、 $\frac{3}{5} \sqrt{5}$

查看试题解析
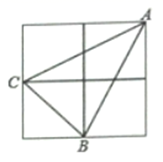12. 如图所示，E．F分别是正方形ABCD的边CD，AD上的点，且CE＝DF，AE，BF相交于点O，下列结论①AE＝BF；②AE⊥BF；③AO＝OE；④S_△AOB＝S_四边形_DEOF中，错误的有（　　）

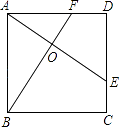A、1个 B、2个 C、3个 D、4个

查看试题解析

二、填空题

13. $\sqrt{12}$ 与最简二次根式5 $\sqrt{a + 1}$ 是同类二次根式，则a= ．

查看试题解析
14. 若 $a + \frac{1}{a} = \sqrt{2} + 1$ ，则 $a^{2} + \frac{1}{a^{2}} =$ ．

查看试题解析
15. 如图，已知在 $Rt △ A B C$ 中， $∠ A C B = 90 °$ ， $A B = 4$ ，分别以 $A C$ ， $B C$ 为直径作半圆，面积分别记为 $S_{1}$ ， $S_{2}$ ，则 $S_{1}$ + $S_{2}$ 的值等于．

查看试题解析
16. 如图，在平行四边形ABCD中，点O是对角线AC ， BD的交点，AC⊥BC ，且AB=10cm，AD=6cm，则AO= cm．

查看试题解析
17. 如图，直线 $l_{1}$ ： $y = x + 2$ 与直线 $l_{2}$ ： $y = k x + b$ 相交于点P（m，4），则方程组 ${\begin{matrix} y = x + 2 \\ y = k x + b \end{matrix}$ 的解是．

查看试题解析
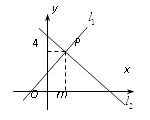18. 如图，两个长宽分别为7cm、3cm的矩形如图叠放在一起，则图中阴影部分的面积是．

查看试题解析
19. 如图，已知菱形ABCD的一个内角∠BAD=80°，对角线AC，BD相交于点O，点E在AB上，且BE=BO，则∠EOA=°.

查看试题解析
20.
如图，定点A（﹣2，0），动点B在直线y=x上运动，当线段AB最短时，点B的坐标为．

查看试题解析

三、解答题

21. 计算

(1)、 $2 \sqrt{20} - \sqrt{5} + 2 \sqrt{\frac{1}{5}}$ ；

(2)、 ${(\sqrt{3} + 2)}^{2} - \sqrt{48} + \sqrt{8} \times \sqrt{\frac{1}{2}}$

查看试题解析

22. 某商场服装部为了调动营业员的积极性，决定实行目标管理，根据目标完成的情况对营业员进行适当的奖励．为了确定一个适当的月销售目标，商场服装部统计了每位营业员在某月的销售额（单位：万元），数据如下：

17	18	16	13	24	15	28	26	18	19
22	17	16	19	32	30	16	14	15	26
15	32	23	17	15	15	28	28	16	19

对这30个数据按组距3进行分组，并整理、描述和分析如下．

频数分布表

组别	一	二	三	四	五	六	七
销售额		$16 ⩽ x < 19$	$19 ⩽ x < 22$	$22 ⩽ x < 25$	$25 ⩽ x < 28$	$28 ⩽ x < 31$	$31 ⩽ x < 34$
频数	7	9	3	a	2	$b$	2

数据分析表

平均数	众数	中位数
20.3	c	18

请根据以上信息解答下列问题：

(1)、填空：a= ， b= ， c=；

(2)、若将月销售额不低于25万元确定为销售目标，则有位营业员获得奖励；

(3)、若想让一半左右的营业员都能达到销售目标，你认为月销售额定为多少合适？说明理由．

查看试题解析

23. 如图，四边形 $A B C D$ 中， $A B = B C = 4$ ， $C D = 6$ ， $D A = 2$ ，且 $∠ B = 90^{\circ}$ .

(1)、求 $A C$ 的长；

(2)、求 $∠ D A B$ 的度数.

查看试题解析
24. 如图，在四边形ABCD中，AB $//$ DC ， AB=AD ，对角线AC ， BD交于点O ， AC平分∠BAD ，过点A作AM⊥CB交CB的延长线于点M ，连接OM ．

(1)、求证：四边形ABCD是菱形；

(2)、若BC= $\sqrt{5}$ ，BD=2，求OM的长．

查看试题解析
25. 我市为了倡导居民节约用水，生活用水按阶梯式水价计费，如图是居民每户每月的水费y(元)与所用的水量x（吨）之间的函数图象，请根据图象所提供的信息，解答下列问题：

(1)、当用水量不超过10吨时，每吨水收费多少元？

(2)、当用水量超过10吨且不超过30吨时，求y与x之间的函数关系式；

(3)、某户居民三、四月份水费共82元，四月份用水比三月份多4吨，求这户居民三月份用水多少吨．

查看试题解析
26. 如图，在平面直角坐标系中，直线 $y = - \frac{1}{2} x + 2$ 与坐标轴交于A ， B两点，以AB为斜边在第一象限内作等腰直角三角形 ABC ，点C为直角顶点，连接OC ．

(1)、求S_△AOB；

(2)、过点C作CE⊥x轴于E点，试探究OB+OA与CE的数量关系，并证明你的结论；

(3)、若M为AB的中点，N为OC的中点，求MN的长．

查看试题解析

17	18	16	13	24	15	28	26	18	19
22	17	16	19	32	30	16	14	15	26
15	32	23	17	15	15	28	28	16	19

17	18	16	13	24	15	28	26	18	19
22	17	16	19	32	30	16	14	15	26
15	32	23	17	15	15	28	28	16	19

17	18	16	13	24	15	28	26	18	19
22	17	16	19	32	30	16	14	15	26
15	32	23	17	15	15	28	28	16	19