山东省聊城市东昌府区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 不能判定四边形ABCD为平行四边形的题设是（）

A、AB＝CD，AB∥CD B、∠A＝∠C，∠B＝∠D C、AB＝AD，BC＝CD D、AB＝CD，AD＝BC

查看试题解析
2. 下面性质中菱形有而矩形没有的是（　　）

A、邻角互补 B、内角和为360° C、对角线相等 D、对角线互相垂直

查看试题解析
3. 在△ABC中，∠A＝25°，∠B＝65°，则下列式子成立的是（　　）

A、AC²+BC²＝AB² B、AB²+BC²＝AC² C、AC²﹣BC²＝AB² D、AC²+AB²＝BC²

查看试题解析
4. 在 $Δ A B C$ 中， $B C : A C : A B = 1 : 1 : \sqrt{2}$ ,则△ABC是（）

A、等腰三角形 B、钝角三角形 C、直角三角形 D、等腰直角三角形

查看试题解析
5. 下列说法中，正确的是（）

A、﹣5是(﹣5)²的算术平方根 B、16的平方根是±4 C、2是﹣4的算术平方根 D、27的立方根是±3

查看试题解析
6. 若a＞b且c为实数，则（）

A、ac＞bc B、ac＜bc C、ac²＞bc² D、ac²≥bc²

查看试题解析
7. 下列二次根式化简后，与 $\sqrt{2}$ 的被开方数相同的是（　　）

A、 $\sqrt{12}$ B、 $\sqrt{\frac{3}{2}}$ C、 $\sqrt{\frac{2}{3}}$ D、 $\sqrt{18}$

查看试题解析
8. 下列说法不一定成立的是（）

A、若a>b，则a+c>b+c B、若a+c>b+c，则a>b C、若a>b，则ac²>bc² D、若ac²>bc² ，则a>b

查看试题解析
9. 若 $\sqrt{2 x - 3}$ 是二次根式，则x应满足的条件是（）

A、x＞ $\frac{3}{2}$ B、x≥ $\frac{3}{2}$ C、x＜ $\frac{3}{2}$ D、x≤ $\frac{3}{2}$

查看试题解析
10. 下列函数中，y是x的一次函数的有（　　）
①y＝x﹣6；②y＝2x²+3；③y＝ $\frac{2}{x}$ ；④y＝ $\frac{x}{8}$ ；⑤y＝x²

A、0个 B、1个 C、2个 D、3个

查看试题解析
11. 已知不等式组 ${\begin{array}{l} x > 2 \\ x < a \end{array}$ 的解集中共有3个整数解，则a的取值范围是（　　）

A、5＜a≤6 B、5≤a＜6 C、5≤a≤6 D、6≤a≤7

查看试题解析
12. 如图所示，直线y＝﹣x+m与y＝nx+4n（n≠0）的交点的横坐标为﹣2，则关于x的不等式﹣x+m＞nx+4n＞0的整数解有（　　）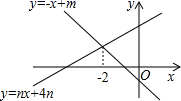

A、1个 B、2个 C、3个 D、无数个

查看试题解析

二、填空题

13. $\sqrt{81}$ 的平方根是．

查看试题解析
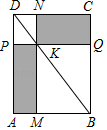
14. 如图，过矩形ABCD的对角线BD上一点K分别作矩形两边的平行线MN与PQ，那么图中矩形AMKP的面积S₁与矩形QCNK的面积S₂的大小关系是S₁S₂；（填“＞”或“＜”或“＝”）

查看试题解析
15. 如图，在▱ABCD中，点E在边AD上，以BE为折痕将△ABE向上翻折，点A正好落在CD的点F处，若△FDE的周长为8，△FCB 的周长为22，则▱ABCD的周长为.

查看试题解析
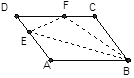16. 已知函数y＝(2m+1)x+m﹣5，若函数图象经过原点，则m的值为．

查看试题解析
17. 若直角三角形的两直角边长为a、b，且满足 $\sqrt{a^{2} - 10 a + 25}$ +|b﹣12|＝0，则该直角三角形的斜边长为．

查看试题解析
18. 若不等式组 ${\begin{array}{l} x - a > 2 \\ b - 2 x > 0 \end{array}$ 的解集是 $- 1 < x < 1$ ，则 ${(a + b)}^{2020} =$ ．

查看试题解析

三、解答题

19. 计算

(1)、 $\frac{x + 6}{3} \leq \frac{x - 3}{2} + 4$

(2)、 ${\begin{array}{l} \frac{2 - 5 x}{6} < \frac{2 x - 3}{2} \\ \frac{1}{2} (x + 4) > 2 \end{array}$

(3)、 $5 \sqrt{\frac{1}{5}} - \sqrt{20} + 2 \sqrt{45}$

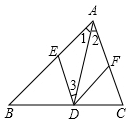
(4)、 ${(- 3)}^{0} - \sqrt{27} + | 1 - \sqrt{2} | + \frac{1}{\sqrt{3} + \sqrt{2}}$

查看试题解析
20. 已知：如图，在△ABC中，AD是∠BAC的平分线，DE∥AC，DF∥AB.求证：四边形AEDF是菱形.

查看试题解析
21. 已知xy＝9，x＞0，y＞0，求 $x \sqrt{\frac{y}{x}} + y \sqrt{\frac{x}{y}}$ 的值．

查看试题解析
22. 如图，在四边形ABCD中，AB＝4，BC＝3，CD＝12，AD＝13，∠B＝90°，求四边形ABCD的面积．

查看试题解析
23. 甲、乙两地相距30km，小李要从甲地到乙地办事，若他以5km/h的速度可按时到达，现在小李走了3h后因有事停留了0.5h，为了不迟到，小李后来的速度至少是多少？

查看试题解析
24. 已知，一次函数y＝（2k﹣1）x+k﹣4，试回答：

(1)、k为何值时，y随x的增大而减小？

(2)、k为何值时，图象与y轴交点在x轴上方？

(3)、若一次函数y＝（2k﹣1）x+k﹣4经过点（1，4）．请求出一次函数的表达式．

查看试题解析
25. 如图，直线l₁：y＝2x+1与直线l₂：y＝mx+4相交于点P（1，b），与x轴交于A，B两点．

(1)、求b，m的值；

(2)、求△ABP的面积．

查看试题解析