山东省聊城冠县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列图形中,既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、 D、
D、 2. 下列命题中,逆命题为真命题的是( )A、菱形的对角线互相垂直 B、矩形的对角线相等 C、平行四边形的对角线互相平分 D、正方形的对角线垂直且相等3. 若 ,则 的值用a、b可以表示为( )A、 B、 C、 D、4. 等式 成立的条件是( )A、 B、 C、x>2 D、5. 如图,在平面直角坐标系中,若点 在直线 与 轴正半轴、 轴正半轴围成的三角形内部,则 的值可能是( )
2. 下列命题中,逆命题为真命题的是( )A、菱形的对角线互相垂直 B、矩形的对角线相等 C、平行四边形的对角线互相平分 D、正方形的对角线垂直且相等3. 若 ,则 的值用a、b可以表示为( )A、 B、 C、 D、4. 等式 成立的条件是( )A、 B、 C、x>2 D、5. 如图,在平面直角坐标系中,若点 在直线 与 轴正半轴、 轴正半轴围成的三角形内部,则 的值可能是( ) A、-3 B、3 C、4 D、56. 如图所示,在Rt△ABC中,AB=AC , D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB , 连接EF , 有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC . 其中正确的有( )
A、-3 B、3 C、4 D、56. 如图所示,在Rt△ABC中,AB=AC , D、E是斜边BC上的两点,且∠DAE=45°,将△ADC绕点A按顺时针方向旋转90°后得到△AFB , 连接EF , 有下列结论:①BE=DC;②∠BAF=∠DAC;③∠FAE=∠DAE;④BF=DC . 其中正确的有( ) A、①②③④ B、②③ C、②③④ D、③④7. 若不等式组 的解集为−1<x<1,则(a−3)(b+3)的值为( )A、1 B、−1 C、2 D、−28. 某种衬衫的进价为400元,出售时标价为550元,由于换季,商店准备打折销售,但要 保持利润不低于10%,那么至多打( )A、6折 B、7折 C、8折 D、9折9. 如图,在 中,D、E分别是 、 的中点, ,F是线段 上一点,连接 、 , ,若 ,则 的长度是( )
A、①②③④ B、②③ C、②③④ D、③④7. 若不等式组 的解集为−1<x<1,则(a−3)(b+3)的值为( )A、1 B、−1 C、2 D、−28. 某种衬衫的进价为400元,出售时标价为550元,由于换季,商店准备打折销售,但要 保持利润不低于10%,那么至多打( )A、6折 B、7折 C、8折 D、9折9. 如图,在 中,D、E分别是 、 的中点, ,F是线段 上一点,连接 、 , ,若 ,则 的长度是( ) A、6 B、8 C、10 D、1210. 如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )A、
A、6 B、8 C、10 D、1210. 如图,两直线y1=kx+b和y2=bx+k在同一坐标系内图象的位置可能是( )A、 B、
B、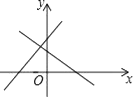 C、
C、 D、
D、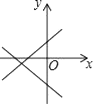 11. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的和最小值为( )
11. 如图,正方形ABCD的面积为16,△ABE是等边三角形,点E在正方形ABCD内,在对角线AC上有一动点P,则PD+PE的和最小值为( ) A、 B、4 C、3 D、12. 小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行 米,先到终点的人原地休息.已知小莹先出发 分钟,在整个步行过程中,两人的距离y(米)与小莹出发的时间t(分)之间的关系如图所示,下列结论:①小莹的步行速度为 米/分;②小亮用 分钟追上小莹;③小亮走完全程用了 分钟;④小亮到达终点时,小莹离终点还有 米.其中正确的结论有( )
A、 B、4 C、3 D、12. 小莹和小亮在笔直的公路上同起点、同终点、同方向匀速步行 米,先到终点的人原地休息.已知小莹先出发 分钟,在整个步行过程中,两人的距离y(米)与小莹出发的时间t(分)之间的关系如图所示,下列结论:①小莹的步行速度为 米/分;②小亮用 分钟追上小莹;③小亮走完全程用了 分钟;④小亮到达终点时,小莹离终点还有 米.其中正确的结论有( ) A、 个 B、 个 C、 个 D、 个
A、 个 B、 个 C、 个 D、 个二、填空题
-
13. 若最简二次根式 和 是同类二次根式,则m= .14. 若函数 与 的图象相交于x轴上的一点,则b的值为 .15. 如图,将周长为10的△ABC沿BC方向平移1个单位得到△DEF , 则四边形ABFD的周长为 .
 16. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为 .
16. 如图,已知函数y1=3x+b和y2=ax﹣3的图象交于点P(﹣2,﹣5),则不等式3x+b>ax﹣3的解集为 . 17. 如图,设四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,如此下去.则第2020个正方形的边长为.
17. 如图,设四边形 是边长为1的正方形,以对角线 为边作第二个正方形 ,再以对角线 为边作第三个正方形 ,如此下去.则第2020个正方形的边长为.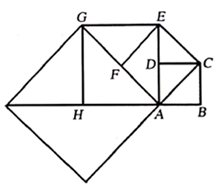
三、解答题
-
18. 计算(1)、 ;(2)、 ;(3)、19. 根据要求解不等式组.(1)、 ;(2)、 (在数轴上把它的解集表示出来).20. 如图所示,已知△ABC的三个顶点的坐标分别为A(-2,3),B(-6,0),C(-1,0).
 (1)、请直接写出点B关于点A对称的点的坐标;(2)、将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.21. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 .
(1)、请直接写出点B关于点A对称的点的坐标;(2)、将△ABC绕坐标原点O逆时针旋转90°,画出图形,直接写出点B的对应点的坐标;(3)、请直接写出:以A、B、C为顶点的平行四边形的第四个顶点D的坐标.21. 如图,四边形 中, ,将 绕点 顺时针旋转一定角度后,点 的对应点恰好与点 重合,得到 .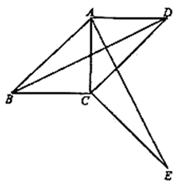 (1)、判断 的形状,并说明理由;(2)、若 , ,试求出四边形 的对角线 的长.22. 某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.(1)、若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.(2)、在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?23. 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF.
(1)、判断 的形状,并说明理由;(2)、若 , ,试求出四边形 的对角线 的长.22. 某商场计划从厂家购进甲、乙两种不同型号的电视机,已知进价分别为:甲种每台1500元,乙种每台2100元.(1)、若商场同时购进这两种不同型号的电视机50台,金额不超过76000元,商场有几种进货方案,并写出具体的进货方案.(2)、在(1)的条件下,若商场销售一台甲、乙型号的电视机的销售价分别为1650元、2300元,以上进货方案中,哪种进货方案获利最多?最多为多少元?23. 过矩形ABCD的对角线AC的中点O作EF⊥AC,交BC边于点E,交AD边于点F,分别连接AE,CF. (1)、求证:四边形AECF是菱形;(2)、若AB=6,AC=10,EC= ,求EF的长.24. 某销售商计划购进甲、乙两种商品共 件进行销售.已知甲种商品每件进价 元,乙种商品每件进价 元;通过市场考察,销售商决定甲种商品以每件 元的价格出售,乙种商品以每件 元的价格出售.设销售商购进的甲种商品有x件,销售完甲、乙两种商品后获得的总利润为y元(1)、求y与x的函数关系式;(2)、如果销售商购进的甲种商品的数量不少于乙种商品数量的 倍,请求出获利最大的进货方案,所获得的最大利润是多少元?25. 如图,在平面直角坐标系中,直线 : 分别与x轴、y轴交于点B、C,且与直线 : 交于点A.
(1)、求证:四边形AECF是菱形;(2)、若AB=6,AC=10,EC= ,求EF的长.24. 某销售商计划购进甲、乙两种商品共 件进行销售.已知甲种商品每件进价 元,乙种商品每件进价 元;通过市场考察,销售商决定甲种商品以每件 元的价格出售,乙种商品以每件 元的价格出售.设销售商购进的甲种商品有x件,销售完甲、乙两种商品后获得的总利润为y元(1)、求y与x的函数关系式;(2)、如果销售商购进的甲种商品的数量不少于乙种商品数量的 倍,请求出获利最大的进货方案,所获得的最大利润是多少元?25. 如图,在平面直角坐标系中,直线 : 分别与x轴、y轴交于点B、C,且与直线 : 交于点A. (1)、求点A、B、C的坐标;(2)、若M是线段 上的点,且 的面积为24,求直线 的函数表达式;(3)、在(2)的条件下,设E是射线 上的点,在平面内是否存在点F,使以O、C、E、F为顶点的四边形是菱形?若存在,直接写出点F的坐标;若不存在,请说明理由.
(1)、求点A、B、C的坐标;(2)、若M是线段 上的点,且 的面积为24,求直线 的函数表达式;(3)、在(2)的条件下,设E是射线 上的点,在平面内是否存在点F,使以O、C、E、F为顶点的四边形是菱形?若存在,直接写出点F的坐标;若不存在,请说明理由.