云南省临沧市2018-2019学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、填空题
-
1. ﹣2的倒数是 .2. 分解因式: -9= .3. 已知点 在正比例函数 的图象上,则 .4. 如图,若 , ,则 .
 5. 如图,在平面直角坐标系中,已知点 , ,菱形 的顶点C在x轴的正半轴上,则对角线 的长为 .
5. 如图,在平面直角坐标系中,已知点 , ,菱形 的顶点C在x轴的正半轴上,则对角线 的长为 . 6. 古希腊数学家把数1,3,6,10,15,……做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,……依此类推,第20个三角形数是 .
6. 古希腊数学家把数1,3,6,10,15,……做三角形数,其中1是第一个三角形数,3是第2个三角形数,6是第3个三角形数,……依此类推,第20个三角形数是 .二、单选题
-
7. 函数 中自变量x的取值范围是( )A、 B、 C、 D、8. 下列几何体中,从左面看到的图形是三角形的是( )A、
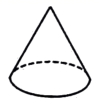 B、
B、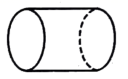 C、
C、 D、
D、 9. 七边形的内角和是( )A、360° B、540° C、720° D、900°10. 下列运算中,正确的是( )A、 B、 C、 D、11. 下列命题中,真命题是( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直且相等的四边形是菱形 C、直角三角形中, 角所对直角边都等于斜边的一半 D、对角线相等的平行四边形是正方形12. 在平面直角坐标系中,若直线 与直线 ( )相交于点 ,则关于x的不等式 的解集是( )A、 B、 C、 D、13. 某同学参加了学校举行的“舞动青春”歌唱比赛,7位评委打分情况如下表:
9. 七边形的内角和是( )A、360° B、540° C、720° D、900°10. 下列运算中,正确的是( )A、 B、 C、 D、11. 下列命题中,真命题是( )A、一组对边平行,另一组对边相等的四边形是平行四边形 B、对角线互相垂直且相等的四边形是菱形 C、直角三角形中, 角所对直角边都等于斜边的一半 D、对角线相等的平行四边形是正方形12. 在平面直角坐标系中,若直线 与直线 ( )相交于点 ,则关于x的不等式 的解集是( )A、 B、 C、 D、13. 某同学参加了学校举行的“舞动青春”歌唱比赛,7位评委打分情况如下表:评委
评委1
评委2
评委3
评委4
评委5
评委6
评委7
打分
6
8
7
8
5
7
8
关于七位评委打分情况,下列说法错误的是( )
A、中位数是7 B、众数是8 C、平均数是7 D、方差是214. 如图,在Rt△ABC中,∠ACB=90°,CD是AB边上的高,CE是AB边上的中线,AD=3,CE=5,则CD等于( ) A、3 B、4 C、 D、
A、3 B、4 C、 D、三、解答题
-
15. 计算: .16. 如图,在 和 中, , , 与 相交于点O.
求证: .
 17. “六一”儿童节前,某玩具商店根据市场调查,用1500元购进一批儿童玩具,上市后很快脱销,接着又用2700元购进第二批,所购数量是第一批数量的1.5倍,但每套进价多了10元,求第二批玩具每套的进价是多少元?18. 某服装厂每天生产A、B两种品牌的服装共600件,已知每件A品牌服装可获利20元,每件B品牌服装可获利15元,设每天生产A品牌服装x件,获得日总利润为y元.(1)、写出y与x之间的函数关系式;(2)、如果服装厂要求每天获利不少于10000元,那么每天至少生产A品牌服装多少件?19. 如图,在平面直角坐标系中, 如图所示.
17. “六一”儿童节前,某玩具商店根据市场调查,用1500元购进一批儿童玩具,上市后很快脱销,接着又用2700元购进第二批,所购数量是第一批数量的1.5倍,但每套进价多了10元,求第二批玩具每套的进价是多少元?18. 某服装厂每天生产A、B两种品牌的服装共600件,已知每件A品牌服装可获利20元,每件B品牌服装可获利15元,设每天生产A品牌服装x件,获得日总利润为y元.(1)、写出y与x之间的函数关系式;(2)、如果服装厂要求每天获利不少于10000元,那么每天至少生产A品牌服装多少件?19. 如图,在平面直角坐标系中, 如图所示.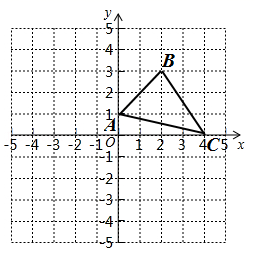
⑴画出把 向下平移3个单位长度,再向左平移4个单位长度得到的 ,并写出 的坐标;
⑵画出把 关于y轴对称的 ,并写出 、 两点坐标.
20. 先化简,再求值: ,其中 .21. 为迎合高中课改,某初级中学对“我最想选择的选修科目是哪一科?”随机抽取了部分学生进行问卷调查,并将调查结果绘制了如下两幅不完整的统计图.请根据图中信息解答下列问题: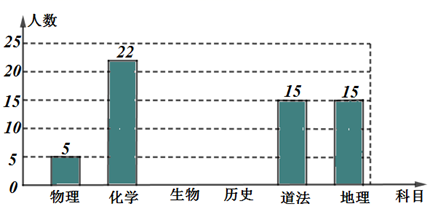
 (1)、本次调查共抽取了多少名学生;(2)、补全条形统计图;(3)、请估计该校2000名学生最想选择的科目是物理的学生人数.
(1)、本次调查共抽取了多少名学生;(2)、补全条形统计图;(3)、请估计该校2000名学生最想选择的科目是物理的学生人数.

