山东省滨州邹平市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 若代数式 在实数范围内有意义,则x的取值范围是( )A、x<3 B、x≤3 C、x>3 D、x≥32. 下列计算中,正确的是( )A、 B、 C、 D、3. 下列命题的逆命题成立的是( )A、对顶角相等 B、全等三角形的对应角相等 C、如果两个实数相等,那么它们的绝对值相等 D、角的内部到角的两边的距离相等的点在角的平分线上4. 已知 中, 分别是 的对边,下列条件中不能判断 是直角三角形的是( )A、 B、 C、 D、5. 如图,在 中,点 分别在边 上.若从下列条件中只选择一个添加到图中的条件中:① ;② ;③ ;④ .那么不能使四边形 是平行四边形的条件相应序号是( )
 A、① B、② C、③ D、④6. 如图,一根木棍 斜靠在与地面 垂直的墙 上,设木棍中点为P,若木棍全端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离将( )
A、① B、② C、③ D、④6. 如图,一根木棍 斜靠在与地面 垂直的墙 上,设木棍中点为P,若木棍全端沿墙下滑,且B沿地面向右滑行.在此滑动过程中,点P到点O的距离将( ) A、变化不定 B、变小 C、不变 D、变大7. 下列式子中,y不是x的函数的是( )A、 B、 C、 D、8. 正比例函数 的函数值y随着x增大而增大,则一次函数 的图象大致是( )A、
A、变化不定 B、变小 C、不变 D、变大7. 下列式子中,y不是x的函数的是( )A、 B、 C、 D、8. 正比例函数 的函数值y随着x增大而增大,则一次函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、 9. 若直线 经过点 和 ,则下列说法正确的是( )A、 B、函数值y随着x增大而减小 C、关于x的方程 的解是 D、关于x的不等式 的解集是10. 某公司招聘职员一名,从学历、经验和工作态度三个方面对甲、乙、丙、丁四名应聘者进行测试.测试结果如下表(各项满分均为10分);
9. 若直线 经过点 和 ,则下列说法正确的是( )A、 B、函数值y随着x增大而减小 C、关于x的方程 的解是 D、关于x的不等式 的解集是10. 某公司招聘职员一名,从学历、经验和工作态度三个方面对甲、乙、丙、丁四名应聘者进行测试.测试结果如下表(各项满分均为10分);应聘者
项目
甲
乙
丙
丁
学历
7
9
7
8
学历
9
8
8
8
工作态度
9
7
9
8
如果将学历、经验和工作态度三项得分按 的比例确定各人的最终得分,并以此为依据录取得分最高者,那么将被录取的是( )
A、甲 B、乙 C、丙 D、丁11. 甲、乙、丙三个旅游团的游客人数都相等,且每个团游客的平均年龄都是 岁,这三个团游客年龄的方差分别是 .导游小方最喜欢带游客年龄相近的旅游团,若在这三个旅游团中选择一个,则他应选( )A、甲团 B、乙团 C、丙团 D、哪一个都可以12. 学习了正方形之后,王老师提出问题:要判断一个四边形是正方形,有哪些思路?甲同学说:先判定四边形是菱形,再确定这个菱形有一个角是直角;
乙同学说:先判定四边形是矩形,再确定这个矩形有一组邻边相等;
丙同学说:判定四边形的对角线相等,并且互相垂直平分;
丁同学说:先判定四边形是平行四边形,再确定这个平行四边形有一个角是直角并且有一组邻边相等.
上述四名同学的说法中,正确的是( )
A、甲、乙 B、甲、丙 C、乙、丙、丁 D、甲、乙、丙、丁二、填空题
-
13. 已知 ,求 .14. 在《九章算术》中有一个问题(如图):今有竹高一丈,末折抵地,去本三尺,问折者高几何?它的意思是:一根竹子原高一丈( 尺),中部一处折断,竹梢触地面处离竹根 尺,试问折断处离地面尺.
 15. 若数据 的平均数为4,则数据 的平均数为 .16. 在学校举行的学生乐器演奏比赛中,八年级的10名学生成绩统计如图所示,则这 名学生成绩的中位数是分.
15. 若数据 的平均数为4,则数据 的平均数为 .16. 在学校举行的学生乐器演奏比赛中,八年级的10名学生成绩统计如图所示,则这 名学生成绩的中位数是分.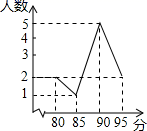 17. 如图, 的周长为 ,对角线 相交于点O,点E是 的中点,则 .
17. 如图, 的周长为 ,对角线 相交于点O,点E是 的中点,则 . 18. 如图,点E为正方形 外一点, 与 相交于点F.若 ,则 .
18. 如图,点E为正方形 外一点, 与 相交于点F.若 ,则 . 19.
19.如图,四边形ABCD是菱形,对角线AC=8cm,DB=6cm,DH⊥AB于点H,则DH的长为 .
 20. 甲骑自行车、乙骑摩托车沿相同路线匀速由 地到 地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行分钟时追上甲.
20. 甲骑自行车、乙骑摩托车沿相同路线匀速由 地到 地,行驶过程中路程与时间的函数关系如图所示.根据图象信息可知,乙在甲骑行分钟时追上甲.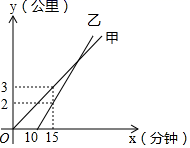
三、解答题
-
21. 计算:22. 学校组织了“我和我的祖国”演讲比赛,甲、乙两队各有 人参加本次比赛,成绩( 分制)如下表所示:
甲
10
8
7
9
8
10
10
9
10
9
乙
7
8
9
7
10
10
9
10
10
10
(1)、甲队成绩的众数是分,乙队成绩的平均数是分.(2)、问哪个队的成绩较为整齐?23. 已知:一条直线经过 三点.求:
(1)、直线 的解析式和a的值;(2)、△AOP的面积.24. 如图, 的对角线 相交于点, ,点P从点A出发,沿 以每秒 个单位的速度向终点D运动.连接 并延长交 于点Q.设点P的运动时间为t秒. (1)、求 的长(用含t的代数式表示);(2)、问t取何值时,四边形 是平行四边形?
(1)、求 的长(用含t的代数式表示);(2)、问t取何值时,四边形 是平行四边形?

