青海省海东市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、填空题
-
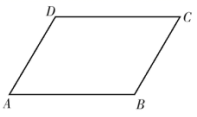
1. 在函数 中,自变量x的取值范围是;化简: .2. 边长为1的正方形的对角线的长为;如图,在 中,若 ,则 的度数为 .
 3. 如图,在 中, 是斜边 上的中线,若 ,则 .
3. 如图,在 中, 是斜边 上的中线,若 ,则 .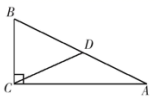 4. 若 与最简二次根式 可以合并,则实数a的值是.5. 将直线y=2x-5向上平移2个单位,所得直线解析式为 .6. 某果园种植甲、乙、丙、丁四个品种的苹果树,为了解每种苹果树的产量情况,从这四个品种中各随机选取10棵进行采摘,经统计,每种苹果树10棵产量的平均数 (单位:kg)及方差S2如表所示:
4. 若 与最简二次根式 可以合并,则实数a的值是.5. 将直线y=2x-5向上平移2个单位,所得直线解析式为 .6. 某果园种植甲、乙、丙、丁四个品种的苹果树,为了解每种苹果树的产量情况,从这四个品种中各随机选取10棵进行采摘,经统计,每种苹果树10棵产量的平均数 (单位:kg)及方差S2如表所示:甲
乙
丙
丁
平均数 (kg)
180
185
190
192
方差S2
7.9
8.2
8.0
7.9
准备从这四个品种中选出一种产量既高又稳定的苹果树进行种植,应选的品种为.
7. 如图,平行四边形ABCD的对角线AC,BD相交于点O,请你添加一个适当的条件使其成为菱形(只填一个即可). 8. 若x,y是变量,且函数 是正比例函数,则k的值为 .9. 已知一个直角三角形三边长的平方和是 ,则斜边长为 .10. 按如图所示的程序计算,若开始输入的n值为 ,则最后输出的结果是
8. 若x,y是变量,且函数 是正比例函数,则k的值为 .9. 已知一个直角三角形三边长的平方和是 ,则斜边长为 .10. 按如图所示的程序计算,若开始输入的n值为 ,则最后输出的结果是 11. 如图,函数 和 的图象相交于点 ,则关于x的不等式 的解集为 .
11. 如图,函数 和 的图象相交于点 ,则关于x的不等式 的解集为 .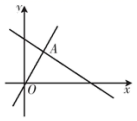 12. 如图所示的是甲、乙两人的运动图象,甲的运动速度乙的运动速度(填“大于”“小于”或“等于”);若甲、乙两人同时出发,相遇时,甲比乙多走千米.
12. 如图所示的是甲、乙两人的运动图象,甲的运动速度乙的运动速度(填“大于”“小于”或“等于”);若甲、乙两人同时出发,相遇时,甲比乙多走千米.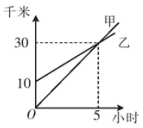
二、单选题
-
13. 若 是二次根式,则a的值不可以是( )A、6 B、﹣3.14 C、 D、2014. 某中学数学兴趣小组10名成员的年龄情况如下:
年龄(岁)
12
13
14
15
人数
1
2
3
4
则这个小组成员年龄的众数和中位数分别是( )
A、15和13.5 B、15和14 C、14和13 D、14和1415. 下列运算正确的是( )A、 B、 C、 D、16. 双十一期间,某超市以优惠价销售 坚果五种礼盒,它们的单价分别为 元、 元, 元, 元, 元,当天销售情况如图所示,则当天销售坚果礼盒的平均售价为( )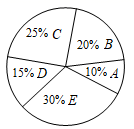 A、 元 B、 元 C、 元 D、 元17. 如图, 的对角线 与 相交于点O,且 .若E是 边的中点, , ,则 的长为( )
A、 元 B、 元 C、 元 D、 元17. 如图, 的对角线 与 相交于点O,且 .若E是 边的中点, , ,则 的长为( )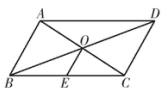 A、 B、 C、 D、18. 下列命题的逆命题是真命题的是( )A、菱形的一条对角线平分一组对角 B、在△ABC中,若AC2+BC2=AB2 , 则△ABC是直角三角形 C、若a 0,则 =a D、平行四边形的对角线互相平分19. 如图,菱形 的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为( )
A、 B、 C、 D、18. 下列命题的逆命题是真命题的是( )A、菱形的一条对角线平分一组对角 B、在△ABC中,若AC2+BC2=AB2 , 则△ABC是直角三角形 C、若a 0,则 =a D、平行四边形的对角线互相平分19. 如图,菱形 的边长是5,O是两条对角线的交点,过O点的三条直线将菱形分成阴影部分和空白部分,若菱形的一条对角线的长为4,则阴影部分的面积为( )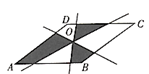 A、 B、 C、12 D、2420. 如图,已知直线 ,过点 作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点 ;过点 作y轴的垂线交直线l于点 ,过点 作直线l的垂线交y轴于点 ,…,按此作法继续下去,则点 的坐标为( )
A、 B、 C、12 D、2420. 如图,已知直线 ,过点 作y轴的垂线交直线l于点B,过点B作直线l的垂线交y轴于点 ;过点 作y轴的垂线交直线l于点 ,过点 作直线l的垂线交y轴于点 ,…,按此作法继续下去,则点 的坐标为( )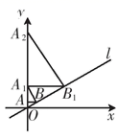 A、 B、 C、 D、
A、 B、 C、 D、三、解答题
-
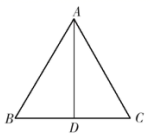
21. 计算:22. 如图,在 中, , ,边 上的中线 ,求证: .
 23. 某学校组织八年级学生在网络上参加传染病防控知识竞赛,试卷共有 道选择题,每题 分,如图所示的是从甲、乙两班各随机抽取的 名学生的得分情况.
23. 某学校组织八年级学生在网络上参加传染病防控知识竞赛,试卷共有 道选择题,每题 分,如图所示的是从甲、乙两班各随机抽取的 名学生的得分情况.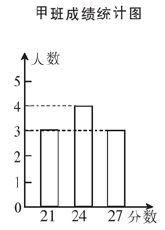
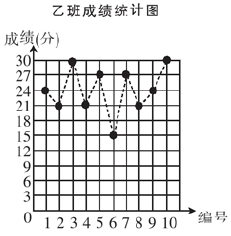 (1)、利用图中提供的信息,补全下表:
(1)、利用图中提供的信息,补全下表:班级
平均数/分
中位数/分
众数/分
甲班
乙班
(2)、若把 分以上(含 分)记为“优秀”,已知两班各有 名学生,请估计两班各有多少名学生成绩为优秀.24. 如图,延长矩形 的边 至点E,使 ,连接 , ,求证: 平分 .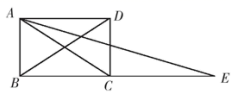 25. 已知直线l平行于直线 ,且经过点 .(1)、求直线l的解析式;(2)、试说明点 是否在直线l上.26. 阅读下列内容:设a , b , c是一个三角形的三条边的长,且a是最长边,我们可以利用a , b , c三条边长度之间的关系来判断这个三角形的形状:①若a2=b2+c2 , 则该三角形是直角三角形;②若a2 b2+c2 , 则该三角形是钝角三角形;③若a2 b2+c2 , 则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,62=36 42+52 , 故由③可知该三角形是锐角三角形,请解答以下问题:(1)、若一个三角形的三边长分别是7,8,9,则该三角形是三角形.(2)、若一个三角形的三边长分别是5,12,x , 且这个三角形是直角三角形,则x的值为 .(3)、若一个三角形的三边长为a= ,b= ,c= ,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.
25. 已知直线l平行于直线 ,且经过点 .(1)、求直线l的解析式;(2)、试说明点 是否在直线l上.26. 阅读下列内容:设a , b , c是一个三角形的三条边的长,且a是最长边,我们可以利用a , b , c三条边长度之间的关系来判断这个三角形的形状:①若a2=b2+c2 , 则该三角形是直角三角形;②若a2 b2+c2 , 则该三角形是钝角三角形;③若a2 b2+c2 , 则该三角形是锐角三角形.例如:若一个三角形的三边长分别是4,5,6,则最长边是6,62=36 42+52 , 故由③可知该三角形是锐角三角形,请解答以下问题:(1)、若一个三角形的三边长分别是7,8,9,则该三角形是三角形.(2)、若一个三角形的三边长分别是5,12,x , 且这个三角形是直角三角形,则x的值为 .(3)、若一个三角形的三边长为a= ,b= ,c= ,其中a是最长边,请判断这个三角形的形状,并写出你的判断过程.