内蒙古兴安盟乌兰浩特市2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 要使二次根式 有意义,则x的取值范围是( )A、x≤﹣3 B、x≥﹣3 C、x≠﹣3 D、x≥32. 下列式子中,属于最简二次根式的是( )A、 B、 C、 D、3. 直角三角形两条直角边长分别是6和8,则斜边上的中线长为( )A、3 B、4 C、5 D、64. 将下列长度的三根木棒首尾顺次连接,能组成直角三角形的是( )A、1,2,3 B、4,6,8 C、6,8,10 D、5,5,45. 已知四边形ABCD是平行四边形,下列结论中错误的是( )A、当AB=BC时,四边形ABCD是菱形 B、当AC⊥BD时,四边形ABCD是菱形 C、当AC=BD时,四边形ABCD是矩形 D、当∠ABC=90°时,四边形ABCD是正方形6. 如图,直线 经过 和 两点,则不等式 的解集为( )
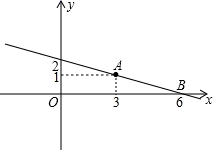 A、 B、 C、 D、7. 若 +(x+3)2=0,则x﹣y的值为( )A、1 B、﹣1 C、7 D、﹣78. 如图,在平行四边形ABCD中,对角线AC,BD相交于O,AC=10cm,AB=4cm,BD⊥AB,则BD的长为( )
A、 B、 C、 D、7. 若 +(x+3)2=0,则x﹣y的值为( )A、1 B、﹣1 C、7 D、﹣78. 如图,在平行四边形ABCD中,对角线AC,BD相交于O,AC=10cm,AB=4cm,BD⊥AB,则BD的长为( ) A、4cm B、.5cm C、6cm D、.8cm9. 已知某一次函数的图象与直线 平行,且过点(3, 7),那么此一次函数为( )A、 B、 C、 D、10. 如图,用若干大小相同的黑白两种颜色的长方形瓷砖,按下列规律铺成一列图案,则第7个图案中黑色瓷砖的个数是( )
A、4cm B、.5cm C、6cm D、.8cm9. 已知某一次函数的图象与直线 平行,且过点(3, 7),那么此一次函数为( )A、 B、 C、 D、10. 如图,用若干大小相同的黑白两种颜色的长方形瓷砖,按下列规律铺成一列图案,则第7个图案中黑色瓷砖的个数是( ) A、19 B、20 C、21 D、2211. 如图,等边 与正方形 重叠,其中D,E两点分别在 , 上,且 ,若 , ,则 的面积为( )
A、19 B、20 C、21 D、2211. 如图,等边 与正方形 重叠,其中D,E两点分别在 , 上,且 ,若 , ,则 的面积为( )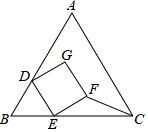 A、1 B、 C、2 D、12. 如图,在 中, , ,点D,E分别是AB, BC的中点,连接DE,CD,如果 ,那么 的周长( )
A、1 B、 C、2 D、12. 如图,在 中, , ,点D,E分别是AB, BC的中点,连接DE,CD,如果 ,那么 的周长( )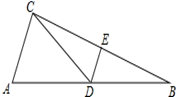 A、28 B、28.5 C、32 D、36
A、28 B、28.5 C、32 D、36二、填空题
-
13. 某公司招聘考试分笔试和面试两项,其中笔试按 ,面试按 计算加权平均数作为总成绩.马丁笔试成绩85分,面试成绩90分,那么马丁的总成绩是分.14. 若菱形两条对角线的长分别是6cm和8cm , 则其面积为cm2 .15. 如图,从数轴的原点O向右数出4个单位,记为点A,过点A作数轴的垂线并截取AB为1个单位长度,连接OB,以点O为圆心,以OB为半径画弧,交数轴的正半轴于点C,则点C所表示的实数为 .
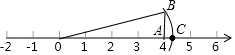 16. 直线y=﹣ x﹣2与两坐标轴围成的三角形面积是 .17. 已知方程组 的解为 ,则直线y=x﹣3与直线y=2x+2的交点坐标为 .18. 如图,正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , ……,按如图的方式放置.点A1 , A2 , A3 , ……和点C1 , C2 , C3……分别在直线y=x +1和x轴上,则点A6的坐标是.
16. 直线y=﹣ x﹣2与两坐标轴围成的三角形面积是 .17. 已知方程组 的解为 ,则直线y=x﹣3与直线y=2x+2的交点坐标为 .18. 如图,正方形A1B1C1O,A2B2C2C1 , A3B3C3C2 , ……,按如图的方式放置.点A1 , A2 , A3 , ……和点C1 , C2 , C3……分别在直线y=x +1和x轴上,则点A6的坐标是.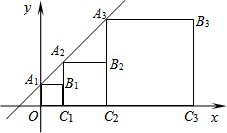
三、解答题
-
19. 计算:(1)、 ;(2)、20. 如图,将长方形ABCD沿EF折叠,使顶点C恰好落在AB边的中点 上.若 , ,求BF的长.
 21. 甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示:
21. 甲、乙两名射击选示在10次射击训练中的成绩统计图(部分)如图所示: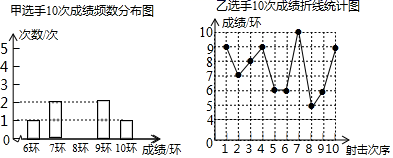
根据以上信息,请解答下面的问题;
选手
A平均数
中位数
众数
方差
甲
a
8
8
c
乙
7.5
b
6和9
2.65
(1)、补全甲选手10次成绩频数分布图.(2)、a= , b= , c= .(3)、教练根据两名选手手的10次成绩,决定选甲选手参加射击比赛,教练的理由是什么?(至少从两个不同角度说明理由).22. 如图,在 中,点D、E分别是边BC、AC的中点,过点A作 交DE的延长线于F点,连接AD、CF.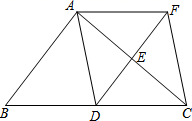 (1)、求证:四边形ADCF是平行四边形;(2)、当 满足什么条件时,四边形图ADCF是菱形?为什么?23. 如图,在平面直角坐标系中,一次函数 的图象与正比例函数 的图象都经过点 .
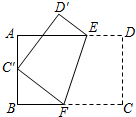
(1)、求证:四边形ADCF是平行四边形;(2)、当 满足什么条件时,四边形图ADCF是菱形?为什么?23. 如图,在平面直角坐标系中,一次函数 的图象与正比例函数 的图象都经过点 .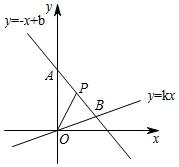 (1)、求一次函数和正比例函数的解析式;(2)、若点 是线段 上一点,且在第一象限内,连接 ,设 的面积为 ,求面积 关于 的函数解析式.24. 6月来临,重庆气温升高,市民购买空调扇的越来越多,根据市场需要,有一电器老板需要购进A,B两种空调扇共200台,已知1台A种空调扇和3台B种空调扇共3800元,2台A种空调扇和1台B种空调扇共2600元.(1)、求A,B两种空调扇的单价;(2)、若需要A种空调扇不少于120台,B种空调扇不少于70台,平均每台空调扇需要运费10元,设购买A种空调扇x台时,总费用y元,求y与x的函数关系式,并直接写出x的取值范围;(3)、求出总费用最少的购置方案.25. 四边形 为正方形,点E为线段 上一点,连接 ,过点E作 ,交射线 于点F,以 、 为邻边作矩形 ,连接 .(1)、如图,求证:矩形 是正方形;
(1)、求一次函数和正比例函数的解析式;(2)、若点 是线段 上一点,且在第一象限内,连接 ,设 的面积为 ,求面积 关于 的函数解析式.24. 6月来临,重庆气温升高,市民购买空调扇的越来越多,根据市场需要,有一电器老板需要购进A,B两种空调扇共200台,已知1台A种空调扇和3台B种空调扇共3800元,2台A种空调扇和1台B种空调扇共2600元.(1)、求A,B两种空调扇的单价;(2)、若需要A种空调扇不少于120台,B种空调扇不少于70台,平均每台空调扇需要运费10元,设购买A种空调扇x台时,总费用y元,求y与x的函数关系式,并直接写出x的取值范围;(3)、求出总费用最少的购置方案.25. 四边形 为正方形,点E为线段 上一点,连接 ,过点E作 ,交射线 于点F,以 、 为邻边作矩形 ,连接 .(1)、如图,求证:矩形 是正方形;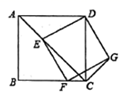 (2)、当线段 与正方形 的某条边的夹角是 时,求 的度数.
(2)、当线段 与正方形 的某条边的夹角是 时,求 的度数.