内蒙古乌兰察布市四子王旗2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列计算正确的是( )A、 B、 C、 D、2. 函数y= 中自变量x的取值范围是( )A、x>3 B、x<3 C、x≤3 D、x≥﹣33. 若正比例函数的图象经过点 ,则这个图象必经过点( )A、 B、 C、 D、4. 的倒数是( )
A、﹣ B、 C、 D、5. 某青年排球队12名队员的年龄情况如表:年龄(单位:岁)
18
19
20
21
22
人数
1
4
3
2
2
则这12名队员的年龄( )
A、众数是19,中位数是19 B、众数是19,中位数是19.5 C、众数是19,中位数是20 D、众数是19,中位数是20.56. 下列二次根式中,不能与 合并的是( )A、 B、 C、 D、7. 四边形ABCD中,对角线AC、BD相交于点O,下列条件不能判定这个四边形是平行四边形的是( )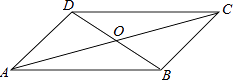 A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC8. 已知正比例函数 的函数值随的增大而增大,则一次函数 的图象大致是( )A、
A、AB∥DC,AD∥BC B、AB=DC,AD=BC C、AO=CO,BO=DO D、AB∥DC,AD=BC8. 已知正比例函数 的函数值随的增大而增大,则一次函数 的图象大致是( )A、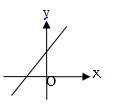 B、
B、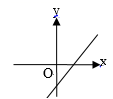 C、
C、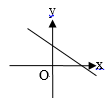 D、
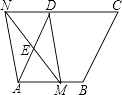
D、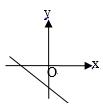 9. 如果直角三角形的边长为3,4,a,则a的值是( )A、5 B、6 C、 D、5或10. 已知点A(﹣2,y1),B(3,y2)在一次函数y=﹣x+b的图象上,则( )A、y1 y2 B、y1 y2 C、y1≤y2 D、y1≥y211. 如图,在▭ABCD 中,BF 平分∠ABC 交 AD 于点 F,CE 平分∠BCD 交 AD 于点 E.若AB=6,EF=2,则 BC 的长为( )
9. 如果直角三角形的边长为3,4,a,则a的值是( )A、5 B、6 C、 D、5或10. 已知点A(﹣2,y1),B(3,y2)在一次函数y=﹣x+b的图象上,则( )A、y1 y2 B、y1 y2 C、y1≤y2 D、y1≥y211. 如图,在▭ABCD 中,BF 平分∠ABC 交 AD 于点 F,CE 平分∠BCD 交 AD 于点 E.若AB=6,EF=2,则 BC 的长为( )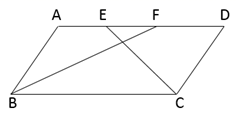 A、6 B、8 C、10 D、1212. 下列说法:
A、6 B、8 C、10 D、1212. 下列说法:①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有( )个.
A、4 B、3 C、2 D、1二、填空题
-
13. 计算: + = .14. 甲、乙两人进行射击测试,每人10次射击成绩的平均数都是8.5环,方差分别是:
S甲2=2,S乙2=1.5,则射击成绩较稳定的是(填“甲”或“乙“).
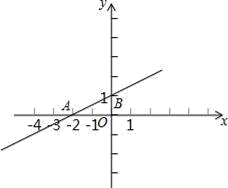
15. 若 的三边长分别是6、8、10,则最长边上的中线长为.16. 如图,直线y=3x和y=kx+2相交于点P(a,3),则关于x不等式(3﹣k)x≤2的解集为.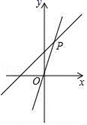 17. 如图所示,在数轴上点 所表示的数为 ,则 的值为 .
17. 如图所示,在数轴上点 所表示的数为 ,则 的值为 .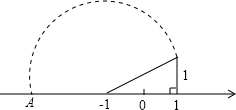 18. 如图中,四边形 ABCD是对角线互相垂直的四边形,且 OB=OD,若使四边形 ABCD为菱形,则需添加的条件是 . (只需添加一个条件即可)
18. 如图中,四边形 ABCD是对角线互相垂直的四边形,且 OB=OD,若使四边形 ABCD为菱形,则需添加的条件是 . (只需添加一个条件即可)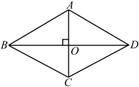 19. 如果直线l与直线y=﹣2x+1平行,与直线y=﹣x+2的交点纵坐标为1,那么直线l的函数解析式为.20. 如图, ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为
19. 如果直线l与直线y=﹣2x+1平行,与直线y=﹣x+2的交点纵坐标为1,那么直线l的函数解析式为.20. 如图, ABCD的顶点B在矩形AEFC的边EF上,点B与点E、F不重合.若△ACD的面积为3,则图中的阴影部分两个三角形的面积和为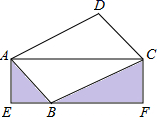
三、解答题
-
21. 计算:(1)、 ;(2)、 .22. 已知一次函数y=kx+b的图象经过点A(-3,-2)及点B(0,4).(1)、求此一次函数的解析式;(2)、当y=-5时求x的值;(3)、求此函数图象与两坐标轴所围成的三角形的面积.23. 如图,E、F分别是矩形ABCD的边 BC、AD上的点,且BE = DF.
 (1)、求证:四边形 AECF 是平行四边形;(2)、若四边形 AECF 是菱形,且 CE = 10,AB = 8,求线段BE的长.
(1)、求证:四边形 AECF 是平行四边形;(2)、若四边形 AECF 是菱形,且 CE = 10,AB = 8,求线段BE的长.