内蒙古呼和浩特市新城区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. $\frac{\sqrt{3 - x}}{\sqrt{x + 1}}$ = $\sqrt{\frac{3 - x}{x + 1}}$ 成立的条件是（）

A、x ≥ - 1 B、x ≤ 3 C、-1＜x ≤3 D、-1 ≤ x ≤ 3

查看试题解析
2. 下列命题中，是真命题的是（）

A、四个角相等的菱形是正方形 B、有一个角是直角的四边形是矩形 C、有两边相等的平行四边形是菱形 D、两条对角线互相垂直且相等的四边形是正方形

查看试题解析
3. 下列各组数中不能作为直角三角形的三边长的是( )

A、1，5， 2， 3 B、7，24，25 C、6，8，10 D、9，12，15

查看试题解析
4. 一次函数y=kx+b中，y随x的增大而减小，b＜0，则这个函数的图象不经过（）

A、第一象限 B、第二象限 C、第三象限 D、第四象限

查看试题解析
5. 某男装专卖店老板专营母品牌夹克，店主统计了一周中不同尺码夹克销售情况如下表：

尺码

39

40

41

42

43

平均每天销售量

10

12

20

12

12

如果每件夹克的利润相同，你认为该店主最关注的销售数据是下列统计量中的（）

A、平均数 B、方差 C、众数 D、中位数

查看试题解析
6. 菱形的周长为8cm，高为1cm，则该菱形两邻角度数比为（）

A、3：1 B、4：1 C、5：1 D、6：1

查看试题解析
7. 如图，Rt△ABC中，∠ACB＝90°，若AB＝15cm，则正方形ADEC和正方形BCFG的面积之和为（）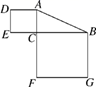

A、150cm² B、200cm² C、225cm² D、无法计算

查看试题解析
8. 实数 $a ， b$ 在数轴上的位置如图所示，则化简 $\sqrt{a^{2}} - \sqrt{b^{2}} - \sqrt{{(a - b)}^{2}}$ 的结果是（）

A、 $- 2 b$ B、 $- 2 a$ C、 $2 (b - a)$ D、0

查看试题解析
9.
如图，在矩形ABCD中，AC、BD相交于点O，AE平分∠BAD交BC于E，若∠EAO=15°，则∠BOE的度数为（　　）

A、85° B、80° C、75° D、70°

查看试题解析
10. 如图，已知一次函数y＝kx+2的图象与x轴，y轴分别交于点A，B，与正比例函数y＝ $\frac{1}{3}$ x交于点C，已知点C的横坐标为2，下列结论：①关于x的方程kx+2＝0的解为x＝3；②对于直线y＝kx+2，当x＜3时，y＞0；③对于直线y＝kx+2，当x＞0时，y＞2；④方程组 ${\begin{array}{l} 3 y - x = 0 \\ y - k x = 2 \end{array}$ 的解为 ${\begin{array}{l} x = 2 \\ y = \frac{2}{3} \end{array}$ ，其中正确的是（）

A、①②③ B、①②④ C、①③④ D、②③④

查看试题解析

二、填空题

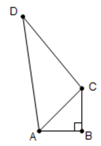
11. 数据2，3，5，5，4的中位数是．

查看试题解析
12. Rt△ABC中∠ABC=90°，斜边AC=10cm，D为斜边上的中点，斜边上的中线BD=.

查看试题解析
13. 如图，在四边形ABCD中，AB=1，BC=1，CD=2， $D A = \sqrt{6} ， ∠ A B C = 90 °$ 则四边形ABCD的面积是．

查看试题解析
14. 已知 $- 1 < a < 0$ ，则 $\sqrt{{(\frac{1}{a} - a)}^{2} + 4} + \sqrt{{(\frac{1}{a} + a)}^{2} - 4} =$ ．

查看试题解析
15. 如图，将矩形纸片ABCD折叠，使点D与点B重合，点C落在 $C^{'}$ 处，折痕为EF，若AB=1，BC=2，则EF= ．

查看试题解析
16. 如图，正方形ABCD中， $∠ D A C$ 的平分线交DC于点E，若P，Q分别是AD和AE上的动点，则DQ+PQ能取得最小值4时，此正方形的边长为．

查看试题解析

三、解答题

17. 按要求回答

(1)、 $\sqrt{\frac{2}{3}} - (\frac{1}{6} \sqrt{24} - \frac{3}{2} \sqrt{12}) + (\sqrt{2} - \sqrt{3}) (\sqrt{2} + \sqrt{3})$ ．

(2)、有一进水管和一出水管容器，从某时刻开始4min内只进水不出水，在随后的8min内既进水又出水，每分的进水量和出水量是两个常数，容器内的水量y与时间x之间的关系如图所示；

①求 $0 \leq x \leq 4$ 时，y随x变化的函数关系式

②当 $4 < x \leq 12$ 时，求y与x的函数解析式；

③每分钟进水、出水各是多少升？

查看试题解析

18. 甲乙两台机床同时生产一种零件，在10天中，两台机床每天出次品的数量如下表：

甲	0	1	0	2	2	0	3	1	2	4
乙	2	3	1	1	0	2	1	1	0	1

(1)、分别计算两组数据的平均数和方差；

(2)、从计算的结果看，在10天中，那台机床出次品的平均数较小？那台机床出次品的波动性较小．

查看试题解析

19. 如图，四边形ABCD是平行四边形，BE//DF且分别交对角线于点E，F，连接ED，BF．
求证： $∠ 1 = ∠ 2$

查看试题解析
20. 在三角形ABC中，AB=13，BC=10，BC边上的中线AD=12，求AC

查看试题解析

21. 灯泡厂为测量一批灯泡的寿命，从中随机抽查了50只灯泡，它们的寿命如表所示：

使用寿命	600≤x＜1000	1000≤x＜1400	1400≤x＜1800	1800≤x＜2200	2200≤x＜2600
灯泡只数	5	10	12	17	6

这批灯泡的平均使用寿命是多少？

查看试题解析

22. 点 $P (x ， y)$ 在第一象限，且 $x + y = 8$ ，点 $A$ 的坐标为 $(6 ， 0)$ ，设 $Δ O P A$ 的面积为 $S$ .

(1)、用含 $x$ 的表达式表示 $S$ ，写出 $x$ 的取值范围，画出函数 $S$ 的图象；

(2)、当点 $P$ 的横坐标为5时， $Δ O P A$ 的面积为多少？

(3)、 $Δ O P A$ 的面积能否大于24？为什么？

查看试题解析
23. 如图，点E，F分别是菱形ABCD的边AB，AD的中点，且AB=5，AC=6，

(1)、 $Δ O E F$ 是什么三角形？证明你的结论；

(2)、求线段EF的长．

查看试题解析
24. 如图 $1$ ，已知直线 $l ： y = - 2 x + 4$ 交 $y$ 轴于点 $A$ ，交 $x$ 轴于点 $B$ ，点 $C (- 3 ， 0)$ ， $D$ 是直线 $l$ 上的一个动点.

(1)、求点 $B$ 的坐标，并求当 $S_{Δ B C D} = S_{Δ B O A}$ 时点 $D$ 的坐标；

(2)、如图 $2$ ，以 $C D$ 为边在 $C D$ 上方作正方形 $C D E F$ ，请画出当正方形 $C D E F$ 的另一顶点也落在直线 $l$ 上的图形，并求出此时 $D$ 点的坐标；

(3)、当 $D$ 点在 $l$ 上运动时，点 $F$ 是否也在某个函数图象上运动?若是请直接写出该函数的解析式；若不在，请说明理由.

查看试题解析

尺码	39	40	41	42	43
平均每天销售量	10	12	20	12	12