内蒙古包头市昆都仑区2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列图形中，既是轴对称图形又是中心对称图形的是（）

A、角 B、线段 C、等边三角形 D、平行四边形

查看试题解析
2. 若m＜n，则下列结论不一定成立的是（）

A、m﹣1＜n﹣1 B、3m＜3n C、﹣ $\frac{m}{4}$ ＞﹣ $\frac{n}{4}$ D、m²＜n²

查看试题解析
3. 已知点A的坐标为（1，3），点B的坐标为（2，1）．将线段AB沿某一方向平移后，点A的对应点的坐标为（﹣2，1）．则点B的对应点的坐标为（）

A、（5，3） B、（﹣1，﹣2） C、（﹣1，﹣1） D、（0，﹣1）

查看试题解析
4. 一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（　　）

A、108° B、90° C、72° D、60°

查看试题解析
5. 把﹣a（x﹣y）﹣b（y﹣x）+c（x﹣y）分解因式正确的结果是（）

A、（x﹣y）（﹣a﹣b+c） B、（y﹣x）（a﹣b﹣c） C、﹣（x﹣y）（a+b﹣c） D、﹣（y﹣x）（a+b﹣c）

查看试题解析
6. 一次函数y=ax+b（a＞0）与x轴的交点坐标为（m ， 0），则一元一次不等式ax+b≤0的解集应为（　　）

A、x≤m B、x≤-m C、x≥m D、x≥-m

查看试题解析
7. 已知下列命题
⑴等边三角形的三个内角都相等；

⑵平行四边形相邻的两个角都相等；

⑶线段垂直平分线上的点到这条线段两个端点距离相等；

⑷底角相等的两个等腰三角形全等．

其中原命题和逆命题均为真命题的有（）

A、1个 B、2个 C、3个 D、4个

查看试题解析
8. 已知四边形ABCD是平行四边形，对角线AC、BD交于点O，E是BC的中点，以下说法错误的是（）

A、OE= $\frac{1}{2}$ DC B、OA=OC C、∠BOE=∠OBA D、∠OBE=∠OCE

查看试题解析
9. 如图，将Rt△ABC绕点A按顺时针方向旋转一定角度得到Rt△ADE，点B的对应点D恰好落在BC边上，若DE＝12，∠B＝60°，则点E与点C之间的距离为（）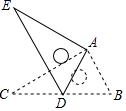

A、12 B、6 C、6 $\sqrt{2}$ D、6 $\sqrt{3}$

查看试题解析
10. 如图，已知：∠MON=30^o ，点A₁、A₂、A₃ 在射线ON上，点B₁、B₂、B₃…．．在射线OM上，△A₁B₁A₂. △A₂B₂A₃、△A₃B₃A₄……均为等边三角形，若OA₁=l，则△A₆B₆A₇ 的边长为（）

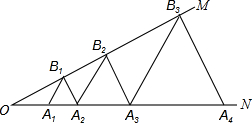A、6 B、12 C、32 D、64

查看试题解析

二、填空题

11. 若分式 $\frac{x^{2} - 9}{x - 3}$ 的值为0，则x的值为．

查看试题解析
12. 如果点P $(3 - m ， 1)$ 在第二象限，则关于x的不等式 $(2 ﹣ m) x + 2 > m$ 的解集是．

查看试题解析
13. 已知关于x的分式方程 $\frac{x}{x - 1}$ ﹣2＝ $\frac{m}{1 - x}$ 的解是正数，则m的取值范围是．

查看试题解析
14. 如图，平行四边形 $A B C D$ 的对角线相交于点 $O$ ，且 $A B \neq A D$ ，过 $O$ 作 $O E ⊥ B D$ 交 $B C$ 于点 $E$ ，若 $△ C D E$ 的周长为10，则平行四边形 $A B C D$ 的周长为 .

查看试题解析
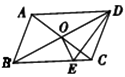15. 如图所示，已知点D为等腰直角三角形ABC内一点，∠CAD=∠CBD=15°，E为AD延长线上的一点，且CE=CA，则∠DCE的度数是．

查看试题解析
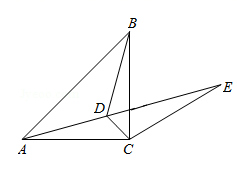16. 如图，AD是△ABC的角平分线，DF⊥AB，垂足为F，DE=DG，△ADG和△AED的面积分别为50和39，则△EDF的面积为．

查看试题解析
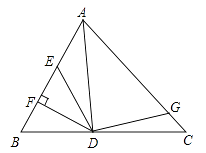17. 如图，以等腰直角三角形ABC的斜边AB为边作等边 $△ A B D$ ，连接DC，以DC为边作等边 $△ D C E$ ，B，E在CD的同侧，若AB＝4 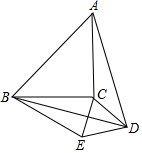$\sqrt{2}$ ，BE的长为．

查看试题解析

三、解答题

18. 解分式方程： $\frac{x - 2}{x + 2}$ ﹣ $\frac{16}{x^{2} - 4}$ ＝ $\frac{x + 2}{x - 2}$ .

查看试题解析
19. 解不等式组 ${\begin{array}{l} \frac{2 x - 1}{3} - \frac{5 x + 1}{2} \leq 1 \\ 5 x - 1 < 3 (x + 1) \end{array}$ 并在数轴上表示出不等式组的解集．

查看试题解析
20. 先化简，再求值： $(\frac{x^{2} - y}{x} - x - 1) \div \frac{x^{2} - y^{2}}{x^{2} - 2 x y + y^{2}}$ ，其中 $x = \sqrt{2} ， y = \sqrt{6}$ ．

查看试题解析
21. 如图，已知△ABC是等边三角形，点D，F分别在线段BC，AB上，∠EFB＝60°，EF＝DC．

(1)、求证：四边形EFCD是平行四边形．

(2)、若BE＝EF，求证：AE＝AD．

查看试题解析
22. 某商家预测一种应季衬衫能畅销市场，就用13200元购进了一批这种衬衫，面市后果然供不应求．商家又用28800元购进了第二批这种衬衫，所购数量是第一批购进量的2倍，但单价贵了10元．

(1)、该商家购进的第一批衬衫是多少件？

(2)、若两批衬衫按相同的标价销售，最后剩下50件按八折优惠卖出，如果两批衬衫全部售完后利润率不低于25%（不考虑其它因素），那么每件衬衫的标价至少是多少元？

查看试题解析
23. 如图1，在Rt△ABC中，∠A＝90°，AB＝AC，点D，E分别在边AB，AC上，AD＝AE，连接DC，点M，P，N分别为DE，DC，BC的中点．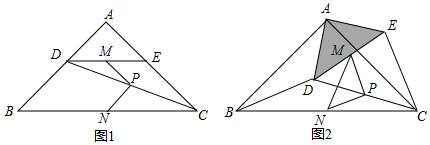

(1)、观察猜想：图1中，线段PM与PN的数量关系是，位置关系是；

(2)、探究证明：把△ADE绕点A逆时针方向旋转到图2的位置，连接MN，BD，CE，判断△PMN的形状，并说明理由；

(3)、拓展延伸：把△ADE绕点A在平面内自由旋转，若AD＝4，AB＝10，请直接写出△PMN面积的最大值．

查看试题解析