辽宁省沈阳市铁西区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列所述图形中,是中心对称图形的是( )
A、直角三角形 B、平行四边形 C、正五边形 D、正三角形2. 若等腰三角形的底角为72°,则这个等腰三角形的顶角的度数是( )A、36° B、54° C、72° D、108°3. 下列各选项中因式分解正确的是( )A、 B、 C、 D、4. 在平面直角坐标系中,点A(2,0),点B(0,1),将线段AB绕点A顺时针旋转60°得到线段AC,则线段BC长为( )A、 B、 C、 D、5. 当a=2020时, 的值是( )A、2021 B、2021.5 C、2020 D、2020.56. 下列说法正确的是( )A、平行四边形的对角线互相垂直 B、对角线互相平分的四边形是平行四边形 C、线段垂直平分线上的点到线段的距离相等 D、同角(或等角)的余角互补7. 不等式组 的解集在数轴上表示正确的是( )A、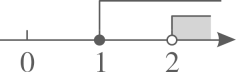 B、
B、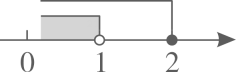 C、
C、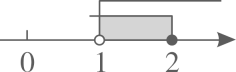 D、
D、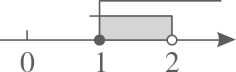 8. 如图,在△ABC中,AC=5,BC= ,BC的垂直平分线DE交AB于点D,交BC于点E.连接CD,若CD⊥AB,则△ABC的面积为( )
8. 如图,在△ABC中,AC=5,BC= ,BC的垂直平分线DE交AB于点D,交BC于点E.连接CD,若CD⊥AB,则△ABC的面积为( ) A、12 B、14 C、24 D、289. 如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的角平分线相交于点P,且∠APB=40°,则∠CBP的度数为( )
A、12 B、14 C、24 D、289. 如图,过正六边形ABCDEF的顶点B作一条射线与其内角∠BAF的角平分线相交于点P,且∠APB=40°,则∠CBP的度数为( ) A、80° B、60° C、40° D、30°10. 如图,点P是△ABC内一点,AP⊥BP,BP=12,CP=15,点D,E,F,G分别是AP,BP,BC,AC的中点,若四边形DEFG的周长为28,则AP长为( )
A、80° B、60° C、40° D、30°10. 如图,点P是△ABC内一点,AP⊥BP,BP=12,CP=15,点D,E,F,G分别是AP,BP,BC,AC的中点,若四边形DEFG的周长为28,则AP长为( ) A、13 B、9 C、5 D、4
A、13 B、9 C、5 D、4二、填空题
-
11. 若分式 的值为0,则x的值是 .12. 因式分解:xy2﹣9x= .13. 如图,在▱ABCD中,AC⊥CD,延长DC到点E,使CE=CD,连接AE,若∠B=60°,AB= ,则△ADE的周长为 .
 14. 如图,直线y=kx+b经过点A(2,﹣1),当kx+b< 时,x的取值范围为 .
14. 如图,直线y=kx+b经过点A(2,﹣1),当kx+b< 时,x的取值范围为 . 15. 在Rt ABC中,∠C=90°,AC=3,AD平分∠BAC交BC于点D,若AD=4,则点D到AB的距离是 .16. 如图,在平面直角坐标系中,△ABO的边OB在x轴上,∠OBA=90°,∠AOB=30°,AB=3,点C是边AB的中点,点D在边OB上,且OD= ,点P为边OA上的动点,当四边形PDBC周长最小时,点P的横坐标为 .
15. 在Rt ABC中,∠C=90°,AC=3,AD平分∠BAC交BC于点D,若AD=4,则点D到AB的距离是 .16. 如图,在平面直角坐标系中,△ABO的边OB在x轴上,∠OBA=90°,∠AOB=30°,AB=3,点C是边AB的中点,点D在边OB上,且OD= ,点P为边OA上的动点,当四边形PDBC周长最小时,点P的横坐标为 .
三、解答题
-
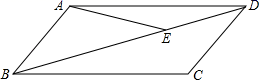
17. 解不等式 .18. 解方程: .19. 已知x=2y﹣6,求﹣3x2+12xy﹣12y2的值.20. 为进一步营造扫黑除恶专项斗争的浓厚宣传氛围,推进平安校园建设,甲、乙两所学校各租用一辆大巴车组织部分师生,分别从距目的地240千米和270千米的两地同时出发,前往“研学教育”基地开展扫黑除恶教育活动,已知乙校师生所乘大巴车的平均速度是甲校师生所乘大巴车的平均速度的1.5倍,甲校师生比乙校师生晚1小时到达目的地,分别求甲、乙两所学校师生所乘大巴车的平均速度.21. 如图,在▱ABCD中,点E是对角线BD上一点,且AB=AE=DE,若∠ABC=51°.求∠DAE的度数.
 22. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C (3,﹣3).
22. 如图,在平面直角坐标系中,已知△ABC的三个顶点坐标分别是A(2,﹣1),B(1,﹣2),C (3,﹣3). (1)、将△ABC向左平移4个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、将△A1B1C1上平移5个单位长度得到△A2B2C2 , 请画出△A2B2C2并直接写出点C2的坐标.23. 某书店最近有A,B两种书比较畅销.近两周的销售情况是:第一周A种书销售数量是15本,B种书销售数量是10本,销售总价是1200元;第二周A种书销售数量是20本,B种书销售数量是10本,销售总价是1450元.(1)、求A,B两种书的销售单价;(2)、若准备用不超过3309元购买这两种书共70本,求最多能购买多少本A种书?
(1)、将△ABC向左平移4个单位长度得到△A1B1C1 , 请画出△A1B1C1;(2)、将△A1B1C1上平移5个单位长度得到△A2B2C2 , 请画出△A2B2C2并直接写出点C2的坐标.23. 某书店最近有A,B两种书比较畅销.近两周的销售情况是:第一周A种书销售数量是15本,B种书销售数量是10本,销售总价是1200元;第二周A种书销售数量是20本,B种书销售数量是10本,销售总价是1450元.(1)、求A,B两种书的销售单价;(2)、若准备用不超过3309元购买这两种书共70本,求最多能购买多少本A种书?

