辽宁省葫芦岛市连山区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列式子中,为最简二次根式的是( )A、 B、 C、 D、2. 若式子 在实数范围内有意义,则x的取值范围是( )A、x≥ B、x> C、x≥ D、x>3. 满足下列条件的 ,不是直角三角形的是( )A、 B、 C、 D、4. 若直角三角形中,斜边的长为13,一条直角边长为5,则这个三角形的面积是( )A、60 B、30 C、20 D、325. 一组数:3,5,4,2,3的中位数是( )A、2 B、3 C、3.5 D、46. 甲、乙两组数据的平均数相等,甲组数据的方差 ,乙组数据的方差 ,则( )A、甲组数据比乙组数据波动大 B、乙组数据比甲组数据波动大 C、甲组数据与乙组数据的波动一样大 D、甲,乙两组数据的数据波动不能比较7. 正比例函数 的函数值 随 的增大而增大,则 的图象大致是( )A、
 B、
B、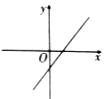 C、
C、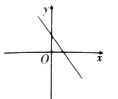 D、
D、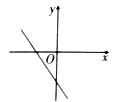 8. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、AB∥CD,AB=CD B、AB=CD,AD=BC C、AB∥CD,∠B=∠D D、AB∥CD,AD=BC9. 如图,折叠长方形的一边 ,使点 落在 边的点 处,若 , ,则 的面积为( )
8. 下列条件中,不能判定四边形ABCD是平行四边形的是( )A、AB∥CD,AB=CD B、AB=CD,AD=BC C、AB∥CD,∠B=∠D D、AB∥CD,AD=BC9. 如图,折叠长方形的一边 ,使点 落在 边的点 处,若 , ,则 的面积为( ) A、 B、 C、 D、10. 甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是( )
A、 B、 C、 D、10. 甲、乙两车从A地出发,匀速驶向B地.甲车以80km/h的速度行驶1h后,乙车才沿相同路线行驶.乙车先到达B地并停留1h后,再以原速按原路返回,直至与甲车相遇.在此过程中,两车之间的距离y(km)与乙车行驶时间x(h)之间的函数关系如图所示.下列说法:①乙车的速度是120km/h;②m=160;③点H的坐标是(7,80);④n=7.5.其中说法正确的是( )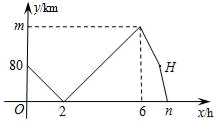 A、①②③ B、①②④ C、①③④ D、①②③④
A、①②③ B、①②④ C、①③④ D、①②③④二、填空题
-
11. = .12. 若一次函数y=(2m﹣1)x+3﹣2m的图象经过一、二、四象限,则m的取值范围是13. 若一组数据1,3,x,4,5,6的平均数是4,则这组数据的众数是 .14. 如图,在平行四边形 中, 平分 ,交 于点 , 平分 ,交 于点 , , ,则 长为 .
 15. 已知一次函数 的图象如图,根据图中信息请写出不等式 的解集为 .
15. 已知一次函数 的图象如图,根据图中信息请写出不等式 的解集为 . 16. 如图,点P是矩形 的对角线 上一点,过点P作 分别交 、 于E、F,连接 , .若 , .则图中阴形部分的面积为.
16. 如图,点P是矩形 的对角线 上一点,过点P作 分别交 、 于E、F,连接 , .若 , .则图中阴形部分的面积为. 17. 如图,一根旗杆在离地面5 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆断裂之前的高为.
17. 如图,一根旗杆在离地面5 m处断裂,旗杆顶部落在离旗杆底部12 m处,旗杆断裂之前的高为. 18. 正方形 ,正方形 ,正方形 ,按如图所示的方式放置在平面直角坐标系中,若点 、 、 和 、 、 …分别在直线 和x轴上,则点 的坐标是 .
18. 正方形 ,正方形 ,正方形 ,按如图所示的方式放置在平面直角坐标系中,若点 、 、 和 、 、 …分别在直线 和x轴上,则点 的坐标是 .
三、解答题
-
19. 计算:(1)、 ;(2)、20. 先化简,再求值: ,其中 .21. 为了了解某公司员工的年收入情况,随机抽查了公司部分员工年收入情况并绘制如图所示统计图.
 (1)、请按图中数据补全条形图;(2)、由图可知员工年收入的中位数是 , 众数是;(3)、估计该公司员工人均年收入约为多少元?22. 如图,在四边形 中, ∥ , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 .
(1)、请按图中数据补全条形图;(2)、由图可知员工年收入的中位数是 , 众数是;(3)、估计该公司员工人均年收入约为多少元?22. 如图,在四边形 中, ∥ , ,对角线 , 交于点 , 平分 ,过点 作 交 的延长线于点 ,连接 . (1)、求证:四边形 是菱形;(2)、若 , ,求线段 的长.23. 一次函数的图象与x轴交于点A(1,0),与y轴交于点B(0,-2).
(1)、求证:四边形 是菱形;(2)、若 , ,求线段 的长.23. 一次函数的图象与x轴交于点A(1,0),与y轴交于点B(0,-2).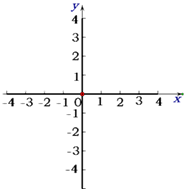 (1)、一次函数的函数关系式;(2)、若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;24. 某经销商从市场得知如下信息:
(1)、一次函数的函数关系式;(2)、若直线AB上有一点C,且△BOC的面积为2,求点C 的坐标;24. 某经销商从市场得知如下信息:某品牌空调扇
某品牌电风扇
进价(元/台)
700
100
售价(元/台)
900
160
他现有40000元资金可用来一次性购进该品牌空调扇和电风扇共100台,设该经销商购进空调扇 台,空调扇和电风扇全部销售完后获得利润为 元.
(1)、求 关于 的函数解析式;(2)、利用函数性质,说明该经销商如何进货可获利最大?最大利润是多少元?25. 如图,已知直线y= +1与x轴、y轴分别交于点A、B,以线AB为直角边在第一象限内作等腰Rt△ABC,∠BAC=90o、点P(x、y)为线段BC上一个动点(点P不与B、C重合),设△OPA的面积为S.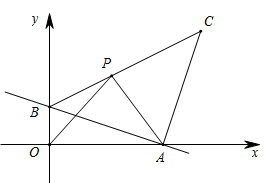 (1)、求点C的坐标;(2)、求S关于x的函数解析式,并写出x的的取值范围;(3)、△OPA的面积能于 吗,如果能,求出此时点P坐标,如果不能,说明理由.26. 如图,在矩形ABCD中,AD=nAB,E,F分别在AB,BC上.
(1)、求点C的坐标;(2)、求S关于x的函数解析式,并写出x的的取值范围;(3)、△OPA的面积能于 吗,如果能,求出此时点P坐标,如果不能,说明理由.26. 如图,在矩形ABCD中,AD=nAB,E,F分别在AB,BC上.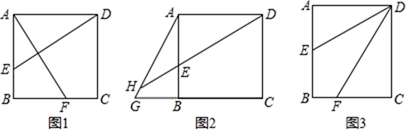 (1)、若n=1,AF⊥DE.
(1)、若n=1,AF⊥DE.①如图1,求证:AE=BF;
②如图2,点G为CB延长线上一点,DE的延长线交AG于H,若AH=AD,求证:AE+BG=AG;
(2)、如图3,若E为AB的中点,∠ADE=∠EDF.求 的值.(结果用含n的式子表示).