辽宁省大连市沙河口区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 的值等于( )
A、4 B、2 C、±2 D、±42. 若直角三角形中,斜边的长为13,一条直角边长为5.则另一条直角边为( )A、 B、 C、 D、3. 若平行四边形中两个内角的度数比为1:2,则其中较小的内角是( )A、60° B、90° C、120° D、45°4. 下列各点在直线 的图象上是( )A、 B、 C、 D、5. 下列计算结果正确的是( )A、 B、 C、 D、6. 下列说法中,错误的是A、平行四边形的对角线互相平分 B、菱形的对角线互相垂直 C、矩形的对角线相等 D、正方形的对角线不一定互相平分7. 下列各式中,是最简二次根式的是( )A、 B、 C、 D、8. 某青年排球队 名队员的年龄情况如下表所示,则这 名队员的平均年龄是( )年龄
人数
A、 岁 B、 岁 C、 岁 D、 岁9. 菱形的周长为8cm,高为1cm,则该菱形两邻角度数比为()A、3:1 B、4:1 C、5:1 D、6:110. 一天早上小明步行上学,他离开家后不远便发现有东西忘在了家里,马上以相同的速度回家去,到家后因事收误一会,忙完后才离开,为了不迟到,小明跑步到了学校,则小明离学校的距离 与离家的时间 之间的函数关系的大致图象是( )A、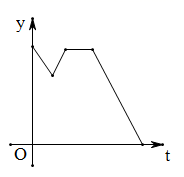 B、
B、 C、
C、 D、
D、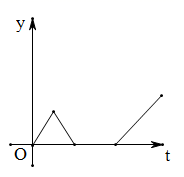
二、填空题
-
11. 使 成立的x的取值范围是 .12. 甲、乙、丙、丁四人进行100m短跑训练,统计近期10次测试的平均成绩都是13.2s,10次测试成绩的方差如下表:则这四人中发挥最稳定的是.
选手
甲
乙
丙
丁
方差(S2)
0.020
0.019
0.021
0.022
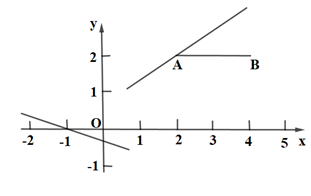
13. 将直线y=2x向下平移3个单位长度得到的直线解析式为.14. 小明向东走 后,沿另一个方向又走了 ,再沿第三个方向走 回到原点.小明向东走 后的方向是 .15. 如图,已知在长方形ABCD中,将△ABE沿着AE折叠至△AEF的位置,点F在对角线AC上,若BE=3,EC=5,则线段CD的长是.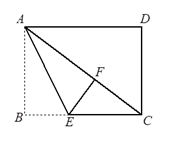 16. 已知一次函数y=x+2与一次函数y=mx+n的图象交于点P(a,-2),则关于x的方程x+2=mx+n的解是 .
16. 已知一次函数y=x+2与一次函数y=mx+n的图象交于点P(a,-2),则关于x的方程x+2=mx+n的解是 .三、解答题
-
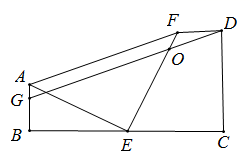
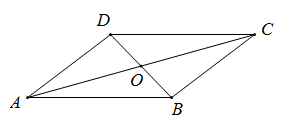
17. 计算:(1)、(2)、18. 已知一次函数 ,当 时 的值为 ,当 时 的值为 ,求一次函数解析式,并画出函数的图象.19. 如图,四边形 中, , 相交于点 , 是 的中点, .求证:四边形 是平行四边形.
 20. 某人买来 只小鸡,经过一段时间精心饲养,可以出售了.下表是这些鸡出售时质量的统计数据
20. 某人买来 只小鸡,经过一段时间精心饲养,可以出售了.下表是这些鸡出售时质量的统计数据质量
频数
(1)、求出售时这些鸡的平均质量;(2)、质量在多少 的鸡最多?中间的鸡质量是多少 ?(3)、分析上表中的数据,写出一条你能得出的结论.21. 某小组要求每两名同学之间都要写评语,小组所有同学一共写了42份评语,这个小组共有学生多少人?22. 现有下面两种移动电话计费方式:方式一
方式二
月租费/(元/月)
本地通话费/(元 )
(1)、以 (单位:分钟)表示通话时间, 单位:元)表示通话费用,分别就两种移动电话计费方式写出 关于 的函数解析式;(2)、何时两种计费方式费用相等;(3)、直接写出如何选择这两种计费方式更省钱.23. 如图,在正方形 中,对角线 与 相交于点 , 为 上一点, , 为 的中点,若 的周长为 .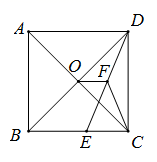 (1)、求 的长;(2)、求 的长.24. 如图,在 中, , , 为 上一点, .点 以每秒 个单位从点 出发滑 向终点 运动,同时点 以秒 个单位从点 出发,沿 运动,当点 到达终点时, 、 同时停止运动.当点 不与点 重合时,过点 作 于点 ,连结 ,以 、 为邻边作 .设 与 重叠部分图形的面积为 ,点 的运动时间为 /秒.
(1)、求 的长;(2)、求 的长.24. 如图,在 中, , , 为 上一点, .点 以每秒 个单位从点 出发滑 向终点 运动,同时点 以秒 个单位从点 出发,沿 运动,当点 到达终点时, 、 同时停止运动.当点 不与点 重合时,过点 作 于点 ,连结 ,以 、 为邻边作 .设 与 重叠部分图形的面积为 ,点 的运动时间为 /秒. (1)、填空: 的长为 .(2)、当 时,求 的值;(3)、求 与 之间的函数关系式.
(1)、填空: 的长为 .(2)、当 时,求 的值;(3)、求 与 之间的函数关系式.