辽宁省大连市甘井子区2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 化简 的结果是( )A、﹣2 B、±2 C、2 D、42. 若二次根式 在实数范围内有意义, 的取值范围是( )A、 B、 C、 D、3. 下列各组数中,不可能成为直角三角形的三条边长的是( )A、 , , B、 , , C、 , , D、 , ,4. 一元二次方程 的根的情况是( )A、无实数根 B、有一个实根 C、有两个相等的实数根 D、有两个不相等的实数根5. 某专卖店专营某品牌的衬衫,店主对上一周中不同尺码的衬衫销售情况统计如下:
尺码
平均每天销售数量(件)
该店主决定本周进货时,增加了一些 码的衬衫,影响该店主决策的统计量是( )
A、平均数 B、方差 C、众数 D、中位数6. 国家实施“精准扶贫”政策以来,很多贫困人口走向了致富的道路.某地区 年底有贫困人口 万人,通过社会各界的努力, 年底贫困人口减少至 万人.设 年底至 年底该地区贫困人口的年平均下降率为 ,根据题意列方程得( )A、 B、 C、 D、7. 如图,矩形 的对角线交于 点.若 , ,则 的长为( ) A、 B、 C、 D、8. “漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( )
A、 B、 C、 D、8. “漏壶”是一种这个古代计时器,在它内部盛一定量的水,不考虑水量变化对压力的影响,水从壶底小孔均匀漏出,壶内壁有刻度.人们根据壶中水面的位置计算时间,用t表示漏水时间,y表示壶底到水面的高度,下列图象适合表示y与x的对应关系的是( ) A、
A、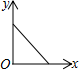 B、
B、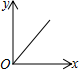 C、
C、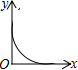 D、
D、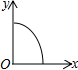 9. 学校篮球队 名场上队员的身高分别为: , , , , (单位: ).增加一名身高为 的成员后,现篮球队成员的身高与原来相比,下列说法正确的是( )A、方差不变 B、方差变大 C、方差变小 D、不能确定10. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 正方形 的边长是 , ,则 的长为( )
9. 学校篮球队 名场上队员的身高分别为: , , , , (单位: ).增加一名身高为 的成员后,现篮球队成员的身高与原来相比,下列说法正确的是( )A、方差不变 B、方差变大 C、方差变小 D、不能确定10. 我国古代数学家刘徽将勾股形(古人称直角三角形为勾股形)分割成一个正方形和两对全等的三角形,如图所示,已知 正方形 的边长是 , ,则 的长为( ) A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 面积为 的正方形的边长是 .12. 在平行四边形 中, ,则 .13.
如图,四边形ABCD的对角线AC、BD相交于点O,且OA=OC,OB=OD.请你添加一个适当的条件: ,使四边形ABCD成为菱形.
 14. 如图,直线 和 的交点是 ,过点 分别作 轴 轴的垂线,则不等式 的解集为 .
14. 如图,直线 和 的交点是 ,过点 分别作 轴 轴的垂线,则不等式 的解集为 . 15. 如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩的方差分别记作 、 ,则 .(填“>”,“=”或“<”)
15. 如图是甲、乙两人6次投篮测试(每次投篮10个)成绩的统计图,甲、乙两人测试成绩的方差分别记作 、 ,则 .(填“>”,“=”或“<”) 16. 如图,在 中, , , 是 的中点, 沿着 方向以每秒 个单位的速度向右匀速运动,当运动时间 秒时, 与 重叠部分的面积为 .
16. 如图,在 中, , , 是 的中点, 沿着 方向以每秒 个单位的速度向右匀速运动,当运动时间 秒时, 与 重叠部分的面积为 .
三、解答题
-
17. 计算(1)、(2)、18. 用适当的方法解方程(1)、(2)、19. 如图,在 中, , , ,求 的周长和面积.
 20. 今年疫情期间,全国各地都积极开展“网上学习”.某研究型学习小为了解该校八年级学生网上学习的情况,从该校八年级随机抽取男女各 名学生,进行了每天网上学习的调查.整理数据后得到如下的表格
20. 今年疫情期间,全国各地都积极开展“网上学习”.某研究型学习小为了解该校八年级学生网上学习的情况,从该校八年级随机抽取男女各 名学生,进行了每天网上学习的调查.整理数据后得到如下的表格学习时间
性别 人数
小时
小时
小时
小时
男生
女生
计算样本数据的平均数、中位数、众数如下表所示:
统计量
性别
平均数
中位数
众数
男生
女生
,
根据以上信息,解答下列问题:
(1)、上表中的 的值为 , 的值为 , 的值为 , 的值为 .(2)、被调查的 名学生每天平均网上学习小时;学习时间的众数是 .(3)、已知该校八年级学生有 名,估计每天网上学习时间不少于 小时的学生人数.21. 如图,在平行四边形 中, 是对角线, 、 是直线 上的点,且 .求证:四边形 是平行四边形. 22. 如图,要为一幅长 、宽 的照片配一个镜框,要求镜框四边的宽度相等,且镜框所占面积为照片面积的 ,镜框的宽度应该多少厘米?(参考: , , , , , , , , )
22. 如图,要为一幅长 、宽 的照片配一个镜框,要求镜框四边的宽度相等,且镜框所占面积为照片面积的 ,镜框的宽度应该多少厘米?(参考: , , , , , , , , ) 23. 在加快“复工复产”的行动中,某通讯运营商的手机上网流量资费标准推出了三种优惠方案:
23. 在加快“复工复产”的行动中,某通讯运营商的手机上网流量资费标准推出了三种优惠方案:方案 :按流量计费, 元 ;
方案 : 元流量套餐包月,包含 流量,如果超过 ,超过部分另外计费(见图象),如果用到 时,超过 的流量不再收费;
方案 : 元包月,无限制使用.
用 表示每月上网流量(单位: ), 表示每月的流量费用(单位:元),方案 和方案 对应的 关于 的函数图象如图所示,请解决以下问题:
 (1)、求方案 的函数解析式,并在图中画出其图象;(2)、若小明奶奶每月使用流量在 之间,请通过计算给出经济合理的选择方案.(3)、小明爸爸根据自己平时使用流量的情况,决定采用最经济的方案是 ,则他每月使用流量最可能的范围是 . (直接写出答案)24. 甲、乙两车将一批抗疫物资从 地运往 地,两车各自的速度都保持匀速行驶.甲出发 后乙开始出发,结果比甲早 到达 地.甲、乙两车离 地的路程 、 与甲车行驶时间行驶的时间 之间的函数关系如图所示.
(1)、求方案 的函数解析式,并在图中画出其图象;(2)、若小明奶奶每月使用流量在 之间,请通过计算给出经济合理的选择方案.(3)、小明爸爸根据自己平时使用流量的情况,决定采用最经济的方案是 ,则他每月使用流量最可能的范围是 . (直接写出答案)24. 甲、乙两车将一批抗疫物资从 地运往 地,两车各自的速度都保持匀速行驶.甲出发 后乙开始出发,结果比甲早 到达 地.甲、乙两车离 地的路程 、 与甲车行驶时间行驶的时间 之间的函数关系如图所示. (1)、求 与 之间的函数关系式;(2)、图中 ; ;(3)、若甲、乙两车之间的路程不小于 ,则 的取值范围是 . (直接写出答案)25. 在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,与直线 交于点 ,
(1)、求 与 之间的函数关系式;(2)、图中 ; ;(3)、若甲、乙两车之间的路程不小于 ,则 的取值范围是 . (直接写出答案)25. 在平面直角坐标系中,直线 与 轴交于点 ,与 轴交于点 ,与直线 交于点 , (1)、当 为 的中点时, 的值为;(2)、当 的面积是 的面积的 倍时,求 的值;(3)、若某菱形的三个顶点是 、 、 ,称此菱形为“亲情菱形”,则“亲情菱形”第四个顶点的坐标为(直接写出答案).26. 如图,在矩形 中, , , 分别在 , 上.(1)、若 ,
(1)、当 为 的中点时, 的值为;(2)、当 的面积是 的面积的 倍时,求 的值;(3)、若某菱形的三个顶点是 、 、 ,称此菱形为“亲情菱形”,则“亲情菱形”第四个顶点的坐标为(直接写出答案).26. 如图,在矩形 中, , , 分别在 , 上.(1)、若 ,①如图, ,求证: ;

②如图,点 为点 关于 的对称点,连结 , 的延长线交 于 ,若 ,猜想 、 、 之间的数量关系,并证明你的猜想.
 (2)、如图,若 、 分别为 、 上的点,求 的最大值(结果用含 的式子表示);
(2)、如图,若 、 分别为 、 上的点,求 的最大值(结果用含 的式子表示); (3)、如图,若 为 的中点, .求 的值(结果用含 的式子表示).
(3)、如图,若 为 的中点, .求 的值(结果用含 的式子表示).