江西省宜春市高安市2019-2020学年八年级下学期数学期末试卷

试卷更新日期：2021-04-28 类型：期末考试

进入出卷网下载

一、单选题

1. 下列各式中，属于最简二次根式的是（）

A、 $\sqrt{5 a^{2} b}$ B、 $x \sqrt{\frac{y}{x}}$ C、 $\sqrt{15}$ D、 $\sqrt{27}$

查看试题解析
2. 下列以线段a、b、c的长为边的三角形中，不能构成直角三角形的是（）

A、 $a = 9, b = 41, c = 40$ B、 $a = 5, b = 5, c = 5 \sqrt{2}$ C、 $a : b : c = 3 : 4 : 5$ D、 $a = 11, b = 12, c = 13$

查看试题解析
3. 要使 $\frac{\sqrt{x + 1}}{2}$ 有意义，则x的取值范围为（）

A、x≤0 B、x≥－1 C、x≥0 D、x≤－1

查看试题解析
4. 某射击运动员在训练中射击了10次，成绩如图所示：

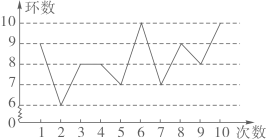
下列结论错误的是（）

A、众数是8 B、中位数是8 C、平均数是8.2 D、方差是1.2

查看试题解析
5. 如图所示是 $5$ 个大小相同的正方形相连，共有正方形的顶点 $12$ 个，从中任取 $4$ 个点为顶点构成正方形，共可以组成正方形的个数为（）

A、 $8$ B、 $9$ C、 $10$ D、 $11$

查看试题解析
6. 直线 $l_{1} ： y = k x + a$ 如图所示，则下列关于直线 $l_{2} ： y = a x + 2 a$ 的说法错误的是（）

A、直线 $l_{2}$ 一定经过点 $(- 2 ， 0)$ B、直线 $l_{2}$ 经过第一、二、三象限 C、直线 $l_{2}$ 与坐标轴围成的三角形的面积为2 D、直线 $l_{2}$ 与直线 $l_{3} ： y = - a x + 2 a$ 关于 $y$ 轴对称

查看试题解析

二、填空题

7. 计算： $(2 \sqrt{\frac{1}{3}}) \cdot (\frac{1}{3} \sqrt{27}) =$ ．

查看试题解析
8. 若一组数据 $4, x, 5, y, 7, 9$ 的平均数为6，众数为5，则这组数据的方差为．

查看试题解析
9. 公元3世纪，我国古代数学家刘徽就能利用近似公式 $\sqrt{a^{2} + r} \approx a + \frac{r}{2 a}$ 得到无理数 $\sqrt{2}$ 的近似数．例如：可将 $\sqrt{2}$ 化为 $\sqrt{1^{2} + 1}$ ，再由近似公式得到 $\sqrt{2} \approx 1 + \frac{1}{2 \times 1} = \frac{3}{2}$ ，若利用此公式计算 $\sqrt{17}$ 的近似值时， $r$ 取正整数，且 $a$ 取尽可能大的正整数，则 $\sqrt{17} \approx$ ．

查看试题解析
10. 如图，直线 $y = k x + b$ 交坐标轴于 $A ， B$ 两点，则不等式 $k x + b > 0$ 的解是．

查看试题解析
11. 如图，矩形 $A B C D$ 中， $A C$ 、 $B D$ 交于点 $O$ ， $M$ 、 $N$ 分别为 $B C$ 、 $O C$ 的中点.若 $M N = 4$ ，则 $A C$ 的长为.

查看试题解析
12. 在平面直角坐标系中， $A (- 4 ， 0)$ ， $B (- 4 ， 8)$ ， $C (0 ， 8)$ ，直线 $y = \frac{4}{3} x + 4$ 与 $O A ， O C$ 分别交于点 $D ， E$ ，若 $P$ 为四边形 $O A B C$ 边上一点（不与点 $D$ 重合），且 $E P = E D$ ，则点 $P$ 的坐标为．

查看试题解析

三、解答题

13. 计算和求证

(1)、计算： $\frac{1}{2} \sqrt{8} - 3 \sqrt{0.5} - \sqrt{4 \frac{1}{2}} + 2 \sqrt{50}$

(2)、在 $▱ A B C D$ 中，点E在边BC上，点F在BC的延长线上，且 $E F = A D$ ，求证： $∠ B A E = ∠ C D F$ ．

查看试题解析
14. 若 $a = \sqrt{5} + 1$ ， $b = \sqrt{5} - 1$ ，求 $a^{2} b + a b^{2}$ 的值．

查看试题解析
15. 图1是围墙的一部分，上部分是由不锈钢管焊成的等腰三角形栅栏如图2，请你根据图2所标注的尺寸，求焊成一个等腰三角形栅栏外框BCD至少需要不锈钢管多少米（焊接部分忽略不计）．

查看试题解析
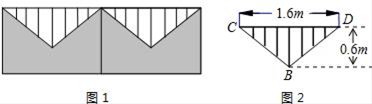16. 如图，过点A（2，0）的两条直线 $l_{1}$ ， $l_{2}$ 分别交y轴于B，C，其中点B在原点上方，点C在原点下方，已知AB= $\sqrt{13}$ .

(1)、求点B的坐标；

(2)、若△ABC的面积为4，求 $l_{2}$ 的解析式.

查看试题解析
17. 如图，矩形ABCD中，点E为边CD上的一点，将矩形ABCD沿BE翻折，点A，D分别落在 $A^{'} ， D^{'}$ 处， $A' B$ 与 $C D$ 相交于点P，请用无刻度的直尺分别按下列要求画图（保留画图痕迹）

(1)、在图1中，作 $∠ B P E$ 的平分线；

(2)、在图2中，过点E作 $A^{'} B$ 的垂线．

查看试题解析

18. 为宣传普及新冠肺炎防治知识，引导学生做好防控．某校举行了主题为“防控新冠，从我做起”的线上知识竞赛活动，测试内容为20道判断题，每道题5分，满分100分，为了解八、九年级学生此次竞赛成绩的情况，分别随机在八、九年级各抽取了20名参赛学生的成绩．已知抽查得到的八年级的数据如下：80，95，75，75，90，75，80，65，80，85，75，65，70，65，85，70，95，80，75，80．

为了便于分析数据，统计员对八年级数据进行了整理，得到了表一：

成绩等级	分数（单位：分）	学生数
D等	60＜x≤70	5
C等	70＜x≤80	a
B等	80＜x≤90	b
A等	90＜x≤100	2

九年级成绩的平均数、中位数、优秀率如下：（分数80分以上、不含80分为优秀）

年级	平均数	中位数	优秀率
八年级	77.5	c	m%
九年级	76	82.5	50%

(1)、根据题目信息填空：a＝， c＝， m＝；

(2)、八年级小宇和九年级小乐的分数都为80分，请判断小宇、小乐在各自年级的排名哪位更靠前？请简述你的理由；

(3)、若九年级共有600人参加参赛，请估计九年级80分以上的人数．

查看试题解析

19. 如图，矩形 $E F G H$ 的顶点 $E ， G$ 分别在菱形 $A B C D$ 的边 $A D ， B C$ 上，顶点 $F ， H$ 在菱形 $A B C D$ 的对角线 $B D$ 上．

(1)、求证： $B G = D E$ ；

(2)、若 $E$ 为 $A D$ 的中点，菱形 $A B C D$ 的周长为8，求 $F H$ 的长度．

查看试题解析
20. 为拓宽学生视野，我市某中学决定组织部分师生租用8辆客车去万载、铜鼓开展研学旅行活动，现有甲、乙两种大客车，它们的租金如表所示．

车型

租金（元/辆）

甲种客车

300

乙种客车

400

(1)、设租用 $x$ 辆乙种客车，租车总费用为 $y$ 元，请求出 $y$ 与 $x$ 的函数关系式；

(2)、在（1）的条件下，学校计划此次研学旅行活动的租车总费用不超过3100元，且租用乙种客车的数量不少于甲种客车的数量，请你求出使租车总费用最少的租车方案及最少费用．

查看试题解析
21. 如图，在 $Δ A B C$ 中， $A C = B C$ ， $∠ A C B > 90^{\circ}$ ， $∠ A B C$ 的平分线交 $A C$ 于 $D$ ， $E$ 是 $A B$ 上的点，且 $B E = B C$ ， $C F / / E D$ 交 $B D$ 于点 $F$ ，连接 $E F ， E D$ ．

(1)、求证：四边形 $C D E F$ 是菱形；

(2)、当 $∠ A C B$ 等于多少度时，四边形 $C D E F$ 是正方形，请给予证明．

查看试题解析
22. 小慧根据学习函数的经验，对函数 $y = | x - 1 |$ 的图像与性质进行了探究．下面是小慧的探究过程，请补充完整：

(1)、函数 $y = | x - 1 |$ 的自变量 $x$ 的取值范围是；

(2)、列表，找出 $y$ 与 $x$ 的几组对应值．

$x$

$\dots$

-1

0

1

2

3

$\dots$

$y$

$\dots$

$b$

1

0

1

2

$\dots$

其中， $b =$ ；

(3)、在平面直角坐标系xOy中，描出上表中以各对对应值为坐标的点，并画出该函数的图象；

(4)、结合函数的图象，解决下列问题．
①写出该函数的两条性质：；

②若 $| x - 1 | \geq x$ ，则x的取值范围为．

查看试题解析
23. 在等边三角形ABC中，点D为直线BC上一动点（点D不与B，C重合），以AD为边在AD的上方作菱形ADEF，且∠DAF=60°，连接CF．

(1)、（观察猜想）如图（1），当点D在线段CB上时，

① $∠ B C F =$ ；

② $B C ， C D ， C F$ 之间数量关系为．

(2)、（数学思考）：如图（2），当点D在线段CB的延长线上时，（1）中两个结论是否仍然成立？请说明理由．

(3)、（拓展应用）：如图（3），当点D在线段BC的延长线上时，若 $A B = 6$ ， $C D = \frac{1}{3} B C$ ，请直接写出 $C F$ 的长及菱形ADEF的面积．

查看试题解析

车型	租金（元/辆）
甲种客车	300
乙种客车	400

$x$	$\dots$	-1	0	1	2	3	$\dots$
$y$	$\dots$	$b$	1	0	1	2	$\dots$