江西省吉安市峡江县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列图形中既是轴对称图形又是中心对称图形的是( )A、
 B、
B、 C、
C、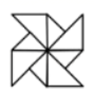 D、
D、 2. 不等式1>3x-2的解集在数轴上表示正确的是( )A、
2. 不等式1>3x-2的解集在数轴上表示正确的是( )A、 B、
B、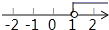 C、
C、 D、
D、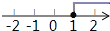 3. 某多边形的每个外角都等于它相邻内角的 ,则这个多边形的边数是( )A、17 B、18 C、19 D、204. 将数字“6”旋转180°,得到数字“9”; 将数字“9”旋转180°,得到数字“6”.现将数学“69”旋转180°,得到的数字是( )A、96 B、69 C、66 D、995. 端午节那天,“90时代”的粽子打9折出售,小马去该店买粽子花了54元钱,比平时多买了3个.求平时每个粽子卖多少元?设平时每个粽子卖x元,列方程为( ).A、 B、 C、 D、6.
3. 某多边形的每个外角都等于它相邻内角的 ,则这个多边形的边数是( )A、17 B、18 C、19 D、204. 将数字“6”旋转180°,得到数字“9”; 将数字“9”旋转180°,得到数字“6”.现将数学“69”旋转180°,得到的数字是( )A、96 B、69 C、66 D、995. 端午节那天,“90时代”的粽子打9折出售,小马去该店买粽子花了54元钱,比平时多买了3个.求平时每个粽子卖多少元?设平时每个粽子卖x元,列方程为( ).A、 B、 C、 D、6.如图,在矩形ABCD中,点E是AD的中点,∠EBC的平分线交CD于点F,将△DEF沿EF折叠,点D恰好落在BE上M点处,延长BC、EF交于点N.有下列四个结论:
①DF=CF;
②BF⊥EN;
③△BEN是等边三角形;
④S△BEF=3S△DEF .
其中,将正确结论的序号全部选对的是( )
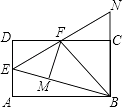 A、①②③ B、①②④ C、②③④ D、①②③④
A、①②③ B、①②④ C、②③④ D、①②③④二、填空题
-
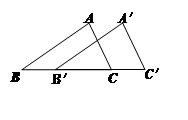
7. 若分式 有意义,则 的取值范围是.8. 因式分解:2m3﹣8m= .9. 如图,△A′B′C′是由△ABC沿BC方向平移2个单位得到的,则点A与点A′的距离等于个单位.
 10.
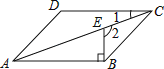
10.如图,在▱ABCD中,BE⊥AB交对角线AC于点E,若∠1=20°,则∠2的度数为 .
 11. 若x+y=10,xy=1 ,则 = .12. 在平面直角坐标系中,将点A(﹣1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是 .13. 已知关于 的不等式组 的整数解共有3个,则 的取值范围是 .14. 四边形ABCD中,∠A=58°,∠C=100°,连结BD,E是AD上一点,连结BE,∠EBD=36°,若点A,C分别在线段BE,BD的垂直平分线上,则∠ADC的度数为 .
11. 若x+y=10,xy=1 ,则 = .12. 在平面直角坐标系中,将点A(﹣1,2)向右平移3个单位长度得到点B,则点B关于x轴的对称点C的坐标是 .13. 已知关于 的不等式组 的整数解共有3个,则 的取值范围是 .14. 四边形ABCD中,∠A=58°,∠C=100°,连结BD,E是AD上一点,连结BE,∠EBD=36°,若点A,C分别在线段BE,BD的垂直平分线上,则∠ADC的度数为 .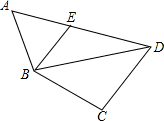 15. 用12根等长的火柴棒拼成一个等腰三角形,火柴棒不允许剩余、重叠、折断,则能摆出不同的等腰三角形的个数为个.16. 如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .
15. 用12根等长的火柴棒拼成一个等腰三角形,火柴棒不允许剩余、重叠、折断,则能摆出不同的等腰三角形的个数为个.16. 如图,已知▱OABC的顶点A、C分别在直线x=1和x=4上,O是坐标原点,则对角线OB长的最小值为 .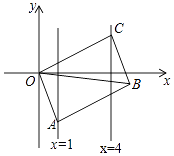
三、解答题
-
17. 解不等式(组),并把解集在数轴上表示出来.(1)、4x-1≥5x-2(2)、18. 解方程:19. 如图,在边长为1个单位长度的小正方形组成的12×12网格中,给出了四边形ABCD的两条边AB与BC,且四边形ABCD是一个轴对称图形,其对称轴为直线AC.
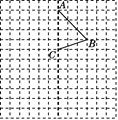
①试在图中标出点D,并画出该四边形的另两条边;
②将四边形ABCD向下平移5个单位长度,画出平移后得到的四边形A′B′C′D′.
20. 先化简: ,然后从 的范围内选取一个合适的整数为 的值代入求值.21. 若关于x的方程 有增根,则增根是多少?并求方程产生增根时m的值.22. 如图,P、Q是△ABC边上的两点,且BP=PQ=QC=AP=AQ,求∠BAC的度数.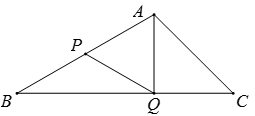 23. 如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,两线相交于点A,已知CD=2,DE=1,求Rt△ABC的面积.
23. 如图,在四边形BCDE中,∠C=∠BED=90°,∠B=60°,延长CD、BE,两线相交于点A,已知CD=2,DE=1,求Rt△ABC的面积. 24. 四边形ABCD中,已知AB∥DC,DB平分∠ADC,∠ADC=∠C=60°,延长CD到点E,连结AE,使得∠C=2∠E.
24. 四边形ABCD中,已知AB∥DC,DB平分∠ADC,∠ADC=∠C=60°,延长CD到点E,连结AE,使得∠C=2∠E.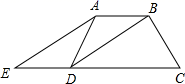 (1)、试判断四边形ABDE的形状,并说明理由;(2)、若AB=8,求CD的长.25. 为发展农村经济,修建一批沼气池.某村共264户村民,村里得到34万元的政府补助款,不足部分由村民集资.修建A型、B型沼气池共20个,两种沼气池每个的修建费用、修建用地、可供使用的户数情况如下表:
(1)、试判断四边形ABDE的形状,并说明理由;(2)、若AB=8,求CD的长.25. 为发展农村经济,修建一批沼气池.某村共264户村民,村里得到34万元的政府补助款,不足部分由村民集资.修建A型、B型沼气池共20个,两种沼气池每个的修建费用、修建用地、可供使用的户数情况如下表:沼气池
修建费用(万元/个)
修建用地(m2/个)
可供使用的户数(户/个)
A型
3
48
20
B型
2
6
3
已知政府只批给该村沼气池修建用地708m2 , 设修建A型沼气池x个,修建两种沼气池共需费用y万元.
(1)、求y与x之间的函数关系式;(2)、不超过政府批给该村沼气池修建用地,又要使该村每户村民都用上沼气的修建方案有哪几种?(3)、若平均每户村民自筹资金700元,能否满足所需费用最少的修建方案?