江西省赣州市大余县2019-2020学年八年级下学期数学期末试卷
试卷更新日期:2021-04-28 类型:期末考试
一、单选题
-
1. 下列式子中,属于最简二次根式的是A、 B、 C、 D、2. 已知▱ABCD的周长为32,AB=4,则BC的长为 ( )
A、4 B、12 C、24 D、283. 下列各组数中,不是勾股数的是( )A、9,12,15 B、12,18,22 C、8,15,17 D、5,12,134. 期中考试后,甲说:“我组成绩是81分的同学最多”,乙说:“我组9人成绩排在最中间的恰好也是81分”,两位同学的话反映的统计量分别为 ( )A、众数和中位数 B、平均数和中位数 C、众数和方差 D、众数和平均数5. 关于函数y= ,下列结论正确的是( )A、函数图象必经过点(1,4) B、函数图象经过二三四象限 C、y随x的增大而增大 D、y随x的增大而减小6.如图,矩形ABCD中,AB=4,BC=3,动点E从B点出发,沿B﹣C﹣D﹣A运动至A点停止,设运动的路程为x,△ABE的面积为y,则y与x的函数关系用图象表示正确的是( )
 A、
A、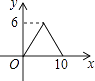 B、
B、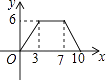 C、
C、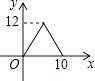 D、
D、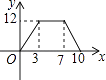
二、填空题
-
7. 若二次根式 有意义,则x的取值范围是 .8. 有一组数据如下:2,3,a,5,6,它们的平均数是4,则这组数据的中位数是 .9. 已知菱形的两条对角线长分别为1和4,则菱形的面积为 .10. 已知:如图,在△ABC中,∠B=30°,∠C=45°, ,则AB的长为 .
 11. 如图,直线l1:y=x+n–2与直线l2:y=mx+n相交于点P(1,2).则不等式mx+n<x+n–2的解集为.
11. 如图,直线l1:y=x+n–2与直线l2:y=mx+n相交于点P(1,2).则不等式mx+n<x+n–2的解集为. 12.
12.如图,在一张长为7cm,宽为5cm的矩形纸片上,现要剪下一个腰长为4cm的等腰三角形(要求:等腰三角形的一个顶点与矩形的一个顶点重合,其余的两个顶点在矩形的边上),则剪下的等腰三角形的面积为 .

三、解答题
-
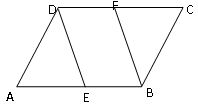
13. 计算:(1)、(2)、14. 如图,在▱ABCD中,E、F分别是AB、CD的中点,求证:四边形EBFD是平行四边形.
 15. 如图,在平面直角坐标系xOy中,O为坐标原点,已知直线l经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB,求直线l的函数解析式.
15. 如图,在平面直角坐标系xOy中,O为坐标原点,已知直线l经过点A(-6,0),它与y轴交于点B,点B在y轴正半轴上,且OA=2OB,求直线l的函数解析式. 16. 如图,在正方形 中,点 是 边上任意一点,请你仅用无刻度的直尺,用连线的方法,分别在图(1)、图(2)中按要求作图(保留作图痕迹,不写作法).
16. 如图,在正方形 中,点 是 边上任意一点,请你仅用无刻度的直尺,用连线的方法,分别在图(1)、图(2)中按要求作图(保留作图痕迹,不写作法). (1)、在如图(1)的 边上求作一点 ,连接 ,使 ;(2)、在如图(2)的 边上求作一点 ,连接 ,使 .17. 如图:四边形ABCD中, AB=BC= , , DA=1, 且AB⊥CB于B.
(1)、在如图(1)的 边上求作一点 ,连接 ,使 ;(2)、在如图(2)的 边上求作一点 ,连接 ,使 .17. 如图:四边形ABCD中, AB=BC= , , DA=1, 且AB⊥CB于B.
试求:
(1)、∠BAD的度数;(2)、四边形ABCD的面积.18. 2019年4月23日世界读书日这天,滨江初二年级的学生会,就2018年寒假读课外书数量(单位:本)做了调查,他们随机调查了甲、乙两个班的10名同学,调查过程如下收集数据
甲、乙两班被调查者读课外书数量(单位:本)统计如下:
甲:1,9,7,4,2,3,3,2,7,2
乙:2,6,6,3,1,6,5,2,5,4
整理、描述数据绘制统计表如下,请补全下表:
班级
平均数
众数
中位数
方差
甲
4
3
乙
6
3.2
分析数据、推断结论
(1)、该校初二乙班共有40名同学,你估计读6本书的同学大概有多少人;(2)、你认为哪个班同学寒假读书情况更好,写出理由.19. 如图,在矩形ABCD中,AB=8,BC=16,点P从点D出发向点A运动,运动到点A停止,同时,点Q从点B出发向点C运动,运动到点C即停止,点P、Q的速度都是每秒1个单位,连接PQ、AQ、CP.设点P、Q运动的时间为t秒 (1)、当t为何值时,四边形ABQP是矩形;(2)、当t=6时,判断四边形AQCP的形状,并说明理由.20. 一次函数 的图象经过点 ,且和正比例函数 的图象交于点 .
(1)、当t为何值时,四边形ABQP是矩形;(2)、当t=6时,判断四边形AQCP的形状,并说明理由.20. 一次函数 的图象经过点 ,且和正比例函数 的图象交于点 . (1)、求一次函数的解析式;(2)、求直线 和两条坐标轴围成的图形面积;(3)、在 轴上求作点 使 最小,求出 点坐标,并求出 的最小值.21. 如图,在 ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE,BD.
(1)、求一次函数的解析式;(2)、求直线 和两条坐标轴围成的图形面积;(3)、在 轴上求作点 使 最小,求出 点坐标,并求出 的最小值.21. 如图,在 ABC中,点F是BC的中点,点E是线段AB的延长线上的一动点,连接EF,过点C作AB的平行线CD,与线段EF的延长线交于点D,连接CE,BD. (1)、求证:四边形DBEC是平行四边形.(2)、若 , ,则在点E的运动过程中:
(1)、求证:四边形DBEC是平行四边形.(2)、若 , ,则在点E的运动过程中:①当BE=时,四边形BECD是矩形,试说明理由;
②当BE=时,四边形BECD是菱形.
22. 为拓宽学生视野,引导学生主动适应社会,我县某中学决定组织部分班级去丫山开展研学旅行活动.在参加此次活动的师生中,若每位老师带17个学生,还剩12个学生没人带;若每位老师带18个学生,就有一位老师少带4个学生,现有甲、乙两种大客车,它们的载客量和租金如下表所示,为了安全既要保证所有师生都有车坐,又要保证每辆车上至少要有2名老师,甲种客车
乙种客车
载客量(人/辆)
30
42
租金(元/辆)
300
400
(1)、参加此次研学旅行活动的老师和学生各有多少人?(2)、设租用两种车共8辆,其中a辆甲种客车,租车总费用为W元.请求出W与a之间的函数关系式(不要求写出a的取值范围);(3)、在(2)的条件下,学校计划此次研学旅行活动的租车总费用不超过3100元,且保证师生都有座位,请问有哪几种不同的租车方案?其中哪种租车方案最省钱?请说明理由.23. 如图1,对角线互相垂直的四边形叫做垂美四边形. (1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.经探究发现垂美四边形ABCD的两组对边AB2 , CD2和AD2 , BC2有一定的数量关系,请你猜想有何种数量关系?并证明.(3)、解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.
(1)、概念理解:如图2,在四边形ABCD中,AB=AD,CB=CD,问四边形ABCD是垂美四边形吗?请说明理由;(2)、性质探究:如图1,四边形ABCD的对角线AC、BD交于点O,AC⊥BD.经探究发现垂美四边形ABCD的两组对边AB2 , CD2和AD2 , BC2有一定的数量关系,请你猜想有何种数量关系?并证明.(3)、解决问题:如图3,分别以Rt△ACB的直角边AC和斜边AB为边向外作正方形ACFG和正方形ABDE,连结CE、BG、GE.已知AC=4,AB=5,求GE的长.