浙教版备考2021年中考数学一轮复习专题30——弧长与扇形

试卷更新日期：2021-04-27 类型：一轮复习

进入出卷网下载

一、单选题

1. 若扇形面积为36 $π$ ，圆心角为120°，则它的弧长为（）

A、 $4 π$ B、 $4 \sqrt{2} π$ C、 $4 \sqrt{3} π$ D、 $8 π$

查看试题解析
2. 圆锥的底面半径为2，母线长为4，则其侧面积为（）

A、 $4 π$ B、 $6 π$ C、 $8 π$ D、 $16 π$

查看试题解析
3. 有一条弧的长为2πcm ，半径为2cm ，则这条弧所对的圆心角的度数是（）

A、90° B、120° C、180° D、135°

查看试题解析
4. 已知圆的半径为 $3,$ 扇形的圆心角为 $60 °$ ，则扇形的面积为（）

A、 $π$ B、 $\frac{3}{2} π$ C、 $2 π$ D、 $3 π$

查看试题解析
5. 如图，⊙A、⊙B、⊙C、⊙D、⊙E相互外离，它们的半径都是1，顺次连接五个圆心得到五边形ABCDE，则图中五个扇形（阴影部分）的面积之和是（）

A、π B、 $\frac{3}{2}$ π C、2π D、4π

查看试题解析
6. 如图，AB是⊙O的直径，弦CD⊥AB，∠CDB＝30°，CD＝2 $\sqrt{3}$ ，则阴影部分图形的面积为（）

A、4π B、2π C、π D、 $\frac{2 π}{3}$

查看试题解析
7. 圆锥的底面半径是5cm，侧面展开图的圆心角是180°，圆锥的高是（）

A、 $5 \sqrt{3}$ cm B、10cm C、6cm D、5cm

查看试题解析
8. 如图，这是一个由圆柱体材料加工而成的零件，它是以圆柱体的上底面为底面，在其内部“掏取”一个与圆柱体等高的圆锥体而得到的，其底面直径 $A B = 12 cm$ ，高 $B C = 8 cm$ ，则这个零件的表面积是（）

A、 $192 π {cm}^{2}$ B、 $196 π {cm}^{2}$ C、 $228 π {cm}^{2}$ D、 $232 π {cm}^{2}$

查看试题解析
9. 如图，在四边形ABCD中，BC=CD=4，AB=7，AB⊥BC，CD⊥BC。把四边形ABCD绕AB旋转一周，则该几何体的表面积为（）

A、48π B、56π C、68π D、72π

查看试题解析
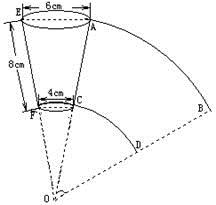
10. 如图，蒙古包可近似看作由圆锥和圆柱组成，若用毛毡搭建一个底面圆面积为25πm² ，圆柱高为3m，圆锥高为2m的蒙古包，则需要毛毡的面积是（）

A、(30+5 $\sqrt{29}$ )πm² B、40πm² C、(30+5 $\sqrt{21}$ )πm² D、55πm²

查看试题解析

二、填空题

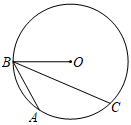
11. 如图，点A，B，C都在⊙O上，若OB=3，∠ABC=30°，则劣弧AC的长为.

查看试题解析
12. 如图，把一个含有30°角的直角三角板ABC绕直角顶点C顺时针旋转90°到 $△ A_{1} B_{1} C$ ，已知 $B C = 2$ ，则在旋转过程中点A经过的路径长为.

查看试题解析
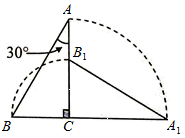13. 已知圆锥的侧面积为8π $c m^{2}$ ，侧面展开图的圆心角为45°，该圆锥的母线长为cm.

查看试题解析
14. 如图是一个圆锥形雪糕冰激凌外壳（不计厚度），已知其母线长为 $12 cm$ ，底面圆半径为 $3 cm$ ．则这个冰激凌外壳的侧面积等于 ${cm}^{2}$ ．（结果保留 $π$ ）

查看试题解析
15. 一根内径为3cm的圆柱形长试管中装满了水，现把试管中的水逐渐滴入一个内径为8cm、高为1.8cm的圆柱形玻璃杯中，当玻璃杯装满水时，试管中的水的高度下降了cm.

查看试题解析
16. 如图，将半径为2，圆心角为120°的扇形OAB绕点B逆时针旋转60°，得到扇形O'A'B，其中点A的运动路径为 $\overset{⌢}{A A^{'}}$ ，则图中阴影部分的面积为.

查看试题解析

三、解答题

17. 如图，在 $△ A B C$ 中，AC＝BC，以BC为直径的⊙O与底边AB交于点D，过点D作DE⊥AC，垂足为点E．

(1)、求证：DE为⊙O的切线；

(2)、若BC＝4，∠A＝30°，求 $\overset{⌢}{D C}$ 的长．（结果保留π）

查看试题解析
18. 现有成135°角且足够长的墙角和可建总长为15m围墙的建筑用料来修建储料场.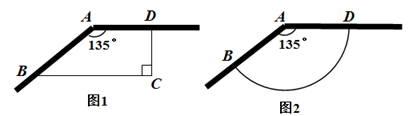

(1)、如图1，修建成四边形ABCD的一个储料场，使 $B C // A D$ ， $∠ C = 90 °$ .新建围墙为BCD.怎样修建围墙才能使储料场的面积最大？最大面积是多少？

(2)、爱动脑筋的小聪建议：把新建的围墙建成如图2所示的以A为圆心的圆弧BD，这样修建的储料场面积会更大.聪明的你认为小聪的建议合理吗？请说明理由.

查看试题解析
19. 如图，方格纸中的每个小方格都是边长为1个单位的正方形.Rt△ABC的顶点均在格点上，建立平面直角坐标系后，点A的坐标为（﹣4，1），点B的坐标为（﹣1，1）.

(1)、先将Rt△ABC向右平移5个单位，再向下平移1个单位后得到Rt△A₁B₁C₁.试在图中画出图形Rt△A₁B₁C₁ ，并写出A₁的坐标；

(2)、将Rt△A₁B₁C₁绕点A₁顺时针旋转90°后得到Rt△A₂B₂C₂ ，试在图中画出图形Rt△A₂B₂C₂.并计算在该旋转过程中Rt△A₁B₁C₁扫过部分的面积.

查看试题解析
20. 有一个直径为2m的圆形铁皮，要从中剪出一个最大的圆心角为90°的扇形ABC．

(1)、求图中阴影部分的面积；

(2)、若将扇形ABC围成一个圆锥，则该圆锥的底面半径最大是多少？

查看试题解析
21. 如图，沿一条母线将圆锥侧面剪开并展平，得到一个扇形，若圆锥的底面圆的半径 $r = 2 cm$ ，扇形的圆心角 $θ = 120 °$ ，求该圆锥的母线长 $l$ ．

查看试题解析
22. 如图，圆锥的底面半径为1，母线长为3，一只蚂蚁要从底面圆周上一点B出发，沿圆锥侧面爬到过母线AB的轴截面上另一母线AC上，问它爬行的最短路线是多少？

查看试题解析
23. 将一个边长为a的正方形纸片卷起来，恰好可以围住一个圆柱的侧面；又在这个正方形纸片上剪下最大的一个扇形，卷起来，恰好可以围住一个圆锥的侧面，那么该圆柱和圆锥两者的底面半径之比为多少？（如果保留π）

查看试题解析
24. 如图是一纸杯，它的母线AC和EF延长后形成的立体图形是圆锥，该圆锥的侧面展开图形是扇形OAB．经测量，纸杯上开口圆的直径是6cm，下底面直径为4cm，母线长为EF=8cm．求扇形OAB的圆心角及这个纸杯的表面积（面积计算结果用表示）．

查看试题解析