浙教版备考2021年中考数学一轮复习专题27——圆的基本性质
试卷更新日期:2021-04-27 类型:一轮复习
一、单选题
-
1. 下列四个命题:①直径所对的圆周角是直角;②圆既是轴对称图形,又是中心对称图形;③在同圆中,相等的圆周角所对的弦相等;④三点确定一个圆.其中正确命题的个数为( )A、1 B、2 C、3 D、42. 下列命题:①垂直于弦的直径平分弦,并且平分弦所对的两条弧;②在同圆或等圆中相等的圆心角所对的弧相等;③在同圆或等圆中如果两条弦相等,那么它们所对的圆心角相等;④圆内接四边形的对角互补.其中正确的命题共有( )A、 个 B、 个 C、 个 D、 个3. 如图,△ABC内接于⊙O,连接AO并延长交BC于点D,若∠B=70°,∠C=50°,则∠ADB的度数是( )
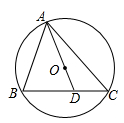 A、70° B、80° C、82° D、85°4. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( )
A、70° B、80° C、82° D、85°4. 如图, 为⊙ 的直径, 为半圆的中点,动点 从点 出发在圆周上顺时针匀速运动,到达点 后停止运动,在点 运动过程中(不包括 、 两点), 的值( ) A、由小逐渐增大 B、固定不变为 C、由大逐渐减小 D、固定不变为5. 矩形 中, , ,如果分别以 、 为圆心的两圆外切,且点 在圆 内,点 在圆 外,那么圆 的半径 的取值范围是( )A、 B、 C、 D、6. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)7. 如图,已知⊙O 的直径 CD=8,AB 是⊙O 的弦,AB⊥CD , 垂足为 M , OM=2,则 AB 的长为( )
A、由小逐渐增大 B、固定不变为 C、由大逐渐减小 D、固定不变为5. 矩形 中, , ,如果分别以 、 为圆心的两圆外切,且点 在圆 内,点 在圆 外,那么圆 的半径 的取值范围是( )A、 B、 C、 D、6. 已知M(1,2),N(3,-3),P(x,y)三点可以确定一个圆,则以下P点坐标不满足要求的是( )A、(3,5) B、(-3,5) C、(1,2) D、(1,-2)7. 如图,已知⊙O 的直径 CD=8,AB 是⊙O 的弦,AB⊥CD , 垂足为 M , OM=2,则 AB 的长为( ) A、2 B、2 C、4 D、48. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )
A、2 B、2 C、4 D、48. 如图是一圆柱形输水管的横截面,阴影部分为有水部分,如果水面AB宽为8cm,水面最深地方的高度为2cm,则该输水管的半径为( )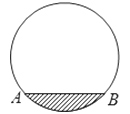 A、3cm B、4cm C、5cm D、6cm9. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )
A、3cm B、4cm C、5cm D、6cm9. 数学课上,老师让学生尺规作图画Rt△ABC,使其斜边AB=c,一条直角边BC=a.小明的作法如图所示,你认为这种作法中判断∠ACB是直角的依据是( )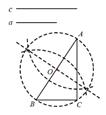 A、勾股定理 B、勾股定理的逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径10. 如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )
A、勾股定理 B、勾股定理的逆定理 C、直径所对的圆周角是直角 D、90°的圆周角所对的弦是直径10. 如图,△ABC中,∠BAC=45°,∠ABC=60°,AB=4,D是边BC上的一个动点,以AD为直径画⊙O分别交AB、AC于点E、F,则弦EF长度的最小值为( )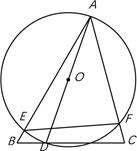 A、 B、 C、2 D、2
A、 B、 C、2 D、2二、填空题
-
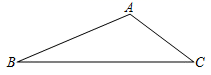
11. 如图,线段BC和动点A构成△ABC,∠BAC=120°,BC=3,则△ABC周长的最大值.
 12. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.
12. 如图,AB是⊙O的直径,AB=4 ,C为弧AB中点,点P是⊙O上一个动点,取弦AP的中点D,则CD的最大值为.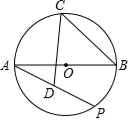 13. 如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于.
13. 如图,在Rt△ABC中,点D为斜边AC上的一点(不与点A、C重合),BD=4,过点A,B,D作⊙O,当点C关于直线BD的对称点落在⊙O上时,则⊙O的半径等于.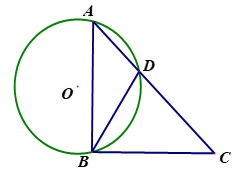 14. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为.
14. 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2 ,则阴影部分图形的面积为.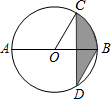 15. 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=米.
15. 赵州桥是我国建筑史上的一大创举,它距今约1400年,历经无数次洪水冲击和8次地震却安然无恙.如图,若桥跨度AB约为40米,主拱高CD约10米,则桥弧AB所在圆的半径R=米. 16. 如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是.
16. 如图,在矩形ABCD中,AB=6,AD=8,以顶点A为圆心作半径为r的圆,若要求另外三个顶点至少有一个在圆内,且至少有一个在圆外,则r的取值范围是.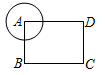
三、解答题
-
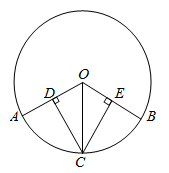
17. 如图: ,CD⊥OA于D,CE⊥OB于E,求证:CD=CE.
 18. 设AB=3cm,画图说明:到点A的距离小于或等于2cm,且到点B的距离大于或等于2cm的所有点组成的图形.19.(1)、如图①,有一个残缺的圆,作出残缺圆的圆心 (保留作图痕迹,不写作法).
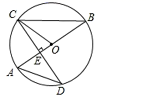
18. 设AB=3cm,画图说明:到点A的距离小于或等于2cm,且到点B的距离大于或等于2cm的所有点组成的图形.19.(1)、如图①,有一个残缺的圆,作出残缺圆的圆心 (保留作图痕迹,不写作法). (2)、如图②,设 是该残缺圆 的弦, 是弧 的中点,若 ,求圆 的半径.
(2)、如图②,设 是该残缺圆 的弦, 是弧 的中点,若 ,求圆 的半径.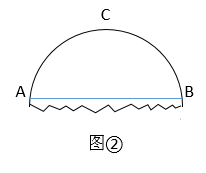 20. 请仅用无刻度的直尺按要求画图(不写作法,保留作图痕迹)
20. 请仅用无刻度的直尺按要求画图(不写作法,保留作图痕迹)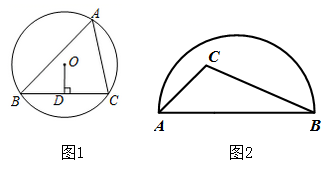 (1)、锐角 是 的内接三角形, 于点 .画出 中 的平分线.(2)、在图2中,点 在半圆内,画出 中 边上的高.21. 如图,四边形 内接于⊙O,AB是直径,点D是 的中点.
(1)、锐角 是 的内接三角形, 于点 .画出 中 的平分线.(2)、在图2中,点 在半圆内,画出 中 边上的高.21. 如图,四边形 内接于⊙O,AB是直径,点D是 的中点.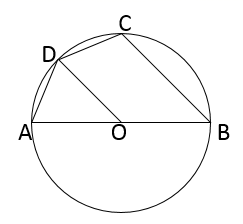 (1)、求证: ;(2)、连结 ,若 ,求 的长.22. 如图,在平面直角坐标系中,一段圆弧上有A、B、C三点的坐标分别为A(0,4),B(4,4),C(6,2).
(1)、求证: ;(2)、连结 ,若 ,求 的长.22. 如图,在平面直角坐标系中,一段圆弧上有A、B、C三点的坐标分别为A(0,4),B(4,4),C(6,2).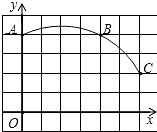 (1)、在图中标出圆弧所在圆的圆心P,且P点坐标为;(2)、⊙P的半径为;∠APC的度数为;点( ,0)在⊙P . (填“上”、“内”、“外”)23. 往水平放置的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB和油的最大深度都为80cm.
(1)、在图中标出圆弧所在圆的圆心P,且P点坐标为;(2)、⊙P的半径为;∠APC的度数为;点( ,0)在⊙P . (填“上”、“内”、“外”)23. 往水平放置的圆柱形油槽内装入一些油后,截面如图所示.若油面宽AB和油的最大深度都为80cm.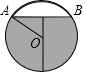 (1)、求油槽的半径OA;(2)、从油槽中放出一部分油,当剩下的油面宽度为60cm时,求油面下降的高度.
(1)、求油槽的半径OA;(2)、从油槽中放出一部分油,当剩下的油面宽度为60cm时,求油面下降的高度.