湘教版备考2021年中考数学二轮复习专题24圆

试卷更新日期：2021-04-27 类型：二轮复习

进入出卷网下载

一、单选题

1. 如图，已知E是 $△ A B C$ 的外心，P，Q分别是 $A B$ ， $A C$ 的中点，连接 $E P$ ， $E Q$ ，分别交 $B C$ 于点F，D.若 $B F = 10$ ， $D F = 6$ ， $C D = 8$ ，则 $△ A B C$ 的面积为（）

A、72 B、96 C、120 D、144

查看试题解析
2. 以半径为1的圆的内接正三角形、正方形、正六边形的边心距为三边作三角形，则（）

A、不能构成三角形 B、这个三角形是等腰三角形 C、这个三角形是直角三角形 D、这个三角形是钝角三角形

查看试题解析
3. 如图，在△ABC中，

（1）作AB和BC的垂直平分线交于点O；（2）以点O为圆心，OA长为半径作圆；（3）⊙O分别与AB和BC的垂直平分线交于点M，N；（4）连接AM，AN，CM，其中AN与CM交于点P.根据以上作图过程及所作图形，下列四个结论：

① $\overset{⌢}{B C}$ ＝2 $\overset{⌢}{N C}$ ；②AB＝2AM；③点P是△ABC的内心；④∠MON＋2∠MPN＝360°.

其中正确结论的个数是（）

A、1 B、2 C、3 D、4

查看试题解析
4. 如图，将边长为6的正六边形铁丝框ABCDEF（面积记为S₁）变形为以点D为圆心，CD为半径的扇形（面积记为S₂），则S₁与S₂的关系为（）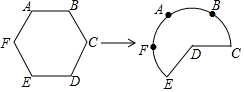

A、S₁＝ $\frac{π}{3}$ S₂ B、S₁＜S₂ C、S₁＝S₂ D、S₁＞S₂

查看试题解析
5. 如图，半径为2cm，圆心角为90°的扇形OAB的弧AB上有一运动的点P，从点P向半径OA引垂线PH交OA于点H。设△OPH的内心为I，当点P在弧AB上从点A运动到点B时，内心I所经过的路径长为（）

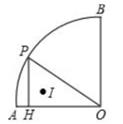A、 $\sqrt{2} π$ B、 $\frac{\sqrt{2}}{2} π$ C、 $\frac{\sqrt{2}}{4} π$ D、π

查看试题解析
6. 如图，⊙O上有一个动点A和一个定点B，令线段AB的中点是点P，过点B作⊙O的切线BQ，且BQ=3，现测得 $\overset{⌢}{A B}$ 的长度是 $\frac{4 π}{3}$ ， $\overset{⌢}{A B}$ 的度数是120°，若线段PQ的最大值是m，最小值是n，则mn的值是（　　）

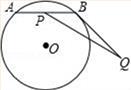A、3 $\sqrt{10}$ B、2 $\sqrt{13}$ C、9 D、10

查看试题解析
7. 如图，AB是⊙o直径，M，N是 $\overset{⌢}{A B}$ 上两点，C是 $\overset{⌢}{M N}$ 上任一点，∠ACB角平分线交⊙o于点D，∠BAC的平分线交CD于点E，当点C从M运动到N时，C、E两点的运动路径长之比为（）

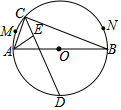A、 $\sqrt{2}$ B、 $\frac{π}{2}$ C、 $\frac{3}{2}$ D、 $\frac{\sqrt{5}}{2}$

查看试题解析
8. 如图，△ABC内接于⊙O，BC=6，AC=2，∠A-∠B=90°，则⊙O的面积为（）

A、9.6π B、10π C、10.8π D、12π

查看试题解析
9. 正六边形的半径与边心距之比为（）

A、1： $\sqrt{3}$ B、 $\sqrt{3}$ ：1 C、 $\sqrt{3}$ ：2 D、2： $\sqrt{3}$

查看试题解析
10. 在 Rt△ABC ，∠C=90°，AB=6．△ABC的内切圆半径为1，则△ABC的周长为（）

A、13 B、14 C、15 D、16

查看试题解析

二、填空题

11. 如图，将半径为2，圆心角为120°的扇形OAB绕点B逆时针旋转60°，得到扇形O'A'B，其中点A的运动路径为 $\overset{⌢}{A A^{'}}$ ，则图中阴影部分的面积为.

查看试题解析
12. 如图所示，将边长为 $8 cm$ 的正方形 $A B C D$ 沿直线 $l$ 向右滚动（不滑动），当正方形滚动两周时（当正方形的四个顶点的位置首次与起始位置相同时，称为正方形滚动一周），正方形的顶点 $A$ 所经过的路线长是 $cm$ ．

查看试题解析
13. 如图，AB为⊙O的直径，C为⊙O上一点，其中AB＝2，∠AOC＝120°，P为⊙O上的动点，连AP，取AP中点Q，连CQ，则线段CQ的最大值为.

查看试题解析
14. 如图，∠AOB=45°，点P、Q都在射线OA上，OP=2，OQ=6.M是射线OB上的一个动点，过P、Q、M三点作圆，当该圆与OB相切时，其半径的长为.

查看试题解析
15. 如图，正六边形 $A_{1} A_{2} A_{3} A_{4} A_{5} A_{6}$ 内部有一个正五形 $B_{1} B_{2} B_{3} B_{4} B_{5}$ ，且 $A_{3} A_{4} // B_{3} B_{4}$ ，直线 $l$ 经过 $B_{2}$ 、 $B_{3}$ ，则直线 $l$ 与 $A_{1} A_{2}$ 的夹角 $α =$ $^{°}$ .

查看试题解析
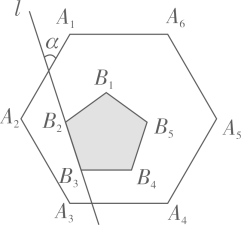16. 如图，有一个圆O和两个正六边形T₁ ， T₂ ． T₁的6个顶点都在圆周上，T₂的6条边都和圆O相切(我们称T₁ ， T₂分别为圆O的内接正六边形和外切正六边形)．若设T₁ ， T₂的边长分别为a，b，圆O的半径为r，则r：a=；r：b=；正六边形T₁ ， T₂的面积比S₁：S₂的值是．

查看试题解析
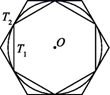17. 如图，扇形AOB，且OB=4，∠AOB=90°，C为弧AB上任意一点，过C点作CD⊥OB于点D，设△ODC的内心为E，连接OE、CE，当点C从点B运动到点A时，内心E所经过的路径长为。

查看试题解析
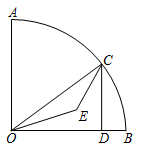18. 如图，⊙O的半径是2，直线1与⊙O相交于A、B两点，M，N是⊙O上的两个动点，且在直线l的异侧，若∠AMB=45°，则四边形MANB的面积最大值是。

查看试题解析
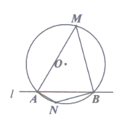19. 如图，在正方形ABCD的边长为3，以A为圆心，2为半径作圆弧．以D为圆心，3为半径作圆弧．若图中阴影部分的面积分为 $S_{1}$ 、 $S_{2}$ ．则 $S_{1} - S_{2}$ =。

查看试题解析
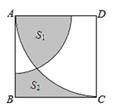20. 如图，作半径为2的⊙O的内接正四边形ABCD，然后作正四边形ABCD的内切圆，得第二个圆，再作第二个圆的内接正四边形A₁B₁C₁D₁ ，又作正四边形A₁B₁C₁D₁的内切圆，得第三个圆…，如此下去，则第六个圆的半径为．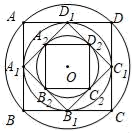

查看试题解析

三、解答题

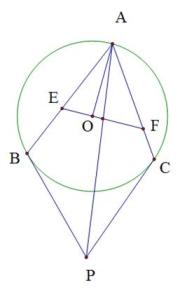
21. 如图，锐角三角形ABC内接于圆O，过圆心O且垂直于半径OA的直线分别交AB、AC于点E、F. 设圆O在B、C两点处的切线交于点P.
证明：直线AP平分线段EF.

查看试题解析
22. 如图所示，圆O为△ABC的外接圆，AM，AT分别为中线和角平分线，过点B和点C的圆O的切线相交于点P，连结AP，与BC和圆O分别相交于点D、E.

求证：点T是△AME的内心。

查看试题解析
23. 如图，AB为⊙O的直径，点C在⊙O外，∠ABC的平分线与⊙O交于点D，∠C=90°．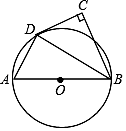

(1)、CD与⊙O有怎样的位置关系？请说明理由；

(2)、若∠CDB=60°，AB=6，求 $\overset{⌢}{A D}$ 的长．

查看试题解析

四、综合题

24.

(1)、问题提出
如图①， $△ A B C$ 内接于半径为4的 $⊙ O$ ， $M N$ 是 $△ A B C$ 的中位线，则 $M N$ 的最大值是；

(2)、问题探究
如图②，在等腰 $△ A B C$ 中， $A B = A C$ ， $∠ B A C = 45 °$ ， $B C$ 边上的中线 $A D = 4 + 2 \sqrt{2}$ ，求等腰 $△ A B C$ 外接圆的半径；

(3)、问题解决
如图③，工人师傅现要在一张足够大的板材上剪裁出一个形状为 $△ A B C$ 的部件，已知 $△ A B C$ 的部件要满足 $∠ B A C = 60 °$ ， $B C$ 边上的中线 $A D = 15 cm$ ，且边 $A B$ 与边 $A C$ 之和要最大，是否能剪裁出满足要求的三角形部件？若能，请求出 $A B + A C$ 的最大值；若不能，请说明理由.

查看试题解析
25. 已知 $P$ 是 $⊙ O$ 上一点，过点 $P$ 作不过圆心的弦 $P Q$ ，在劣弧 $P Q$ 和优弧 $P Q$ 上分别有动点 $A$ 、 $B$ （不与 $P$ 、 $Q$ 重合），连接 $A P$ 、 $B P$ ．若 $∠ A P Q = ∠ B P Q$ ．

(1)、如图1，当 $∠ A P Q = 45 °$ ， $A P = 1$ ， $B P = 2 \sqrt{2}$ 时，求 $⊙ O$ 的半径；

(2)、在（1）的条件下，求四边形 $A P B Q$ 的面积；

(3)、如图2，连接 $A B$ ，交 $P Q$ 于点 $M$ ，点 $N$ 在线段 $P M$ 上（不与 $P$ 、 $M$ 重合），连接 $O N$ 、 $O P$ ，若 $∠ N O P + 2 ∠ O P N = 90 °$ ，探究直线 $A B$ 与 $O N$ 的位置关系，并说明理由．

查看试题解析
26. AB为⊙O的直径，C是⊙O上的一点，D在AB的延长线上，且∠DCB=∠A，

(1)、CD与⊙O相切吗？如果相切，请你加以证明；如果不相切，请说明理由。

(2)、若∠D=30°，BD=10cm，求⊙O的半径。

查看试题解析
27. 如图，在△ABC中，∠C=90°，以BC为直径的⊙O交AB于点D，⊙O的切线DE交AC于点E.

(1)、求证：E是AC中点；

(2)、若AB=10，BC=6，连接CD，OE，交点为F，求OF的长.

查看试题解析
28. 已知AB为⊙O的直径，点C为⊙O上一点，点D为AB延长线一点，连接AC ．

(1)、如图①，OB=BD ，若DC与⊙O相切，求∠D和∠A的大小；

(2)、如图②，CD与⊙O交于点E ， AF⊥CD于点F连接AE ，若∠EAB=18°，求∠FAC的大小．

查看试题解析
29. 已知某种月饼形状的俯视图如图1所示，该形状由1个正六边形和6个半圆组成，半圆直径与正六边形的边长相等.

现商家设计了2种棱柱体包装盒，其底面分别为矩形和正六边形(如图2和图3)我们可从底面的利用率来记算整个包装盒的利用情况.(底面利用率= $\frac{月饼面积}{包装盒底面面积}$ ×100%)

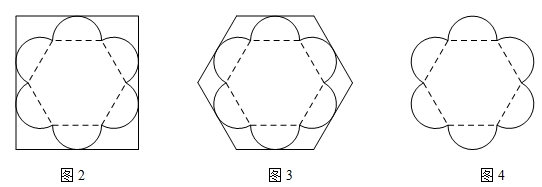(1)、请分别计算出图2与图3中的底面利用率(结果保留到0.1%)；

(2)、考虑到节约成本，商家希望底面利用率能够不低于80%，且底面图形仍然采用最基本的几何形状，请问商家的要求是否能够满足，若可以满足，请设计一种方案，并直接写出此时的利用率；若不能满足，请说明理由.

查看试题解析