湘教版备考2021年中考数学二轮复习专题23二次函数
试卷更新日期:2021-04-27 类型:二轮复习
一、单选题
-
1. 如图,二次函数 (a、b、c是常数,且 )的图象与x轴的一个交点为 ,对称轴为直线 ,下列结论:① ;② ;③ ;④ .其中正确结论的个数为( )
 A、1个 B、2个 C、3个 D、4个2. 已知函数 , (a、b、c为常数),如图所示,y2=ax+b.在研究两个函数时,同学们得到结论如下,其中错误的一个结论为( )
A、1个 B、2个 C、3个 D、4个2. 已知函数 , (a、b、c为常数),如图所示,y2=ax+b.在研究两个函数时,同学们得到结论如下,其中错误的一个结论为( )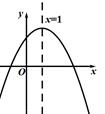 A、 B、当x>3时,ax+b<0 C、当x>2时,y1>y2. D、有两个不同的解3. 已知二次函数y=ax2+bx+4的图象如图所示,下列结论:①abc>0;②a+b+c=2;③b2﹣4ac>0;④a< ;⑤b>1,其中正确结论有( )
A、 B、当x>3时,ax+b<0 C、当x>2时,y1>y2. D、有两个不同的解3. 已知二次函数y=ax2+bx+4的图象如图所示,下列结论:①abc>0;②a+b+c=2;③b2﹣4ac>0;④a< ;⑤b>1,其中正确结论有( )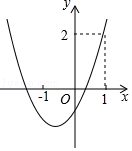 A、2个 B、3个 C、4个 D、5个4. 已知二次函数y=ax2+bx+c的图像与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:①abc>0 ② 4ac-b2>0 ③ a-b+c>0 ④ac+b+1=0.其中正确的个数是( )
A、2个 B、3个 C、4个 D、5个4. 已知二次函数y=ax2+bx+c的图像与x轴分别交于A、B两点,与y轴交于C点,OA=OC,则由抛物线的特征写出如下结论:①abc>0 ② 4ac-b2>0 ③ a-b+c>0 ④ac+b+1=0.其中正确的个数是( ) A、4个 B、3个 C、2个 D、1个5. 如图,二次函数 的图象与x轴交于 两点,与y轴负半轴交于点C,它的对称轴为直线 ,则下列选项中正确的是( )
A、4个 B、3个 C、2个 D、1个5. 如图,二次函数 的图象与x轴交于 两点,与y轴负半轴交于点C,它的对称轴为直线 ,则下列选项中正确的是( ) A、 B、 C、 D、当 为实数)时,6. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( )
A、 B、 C、 D、当 为实数)时,6. 如图,二次函数 的图象与 轴交于两点 , ,其中 .下列四个结论:① ;② ;③ ;④ ,正确的个数是( ) A、1 B、2 C、3 D、47. 如图,抛物线y=ax2+bx+c(a< 0)的图象经过点(1, 2),与x轴交点的横坐标分别为x1 , x2 , 其中-1<x1<0,1<x2<2, 则下列结论中正确的是( )
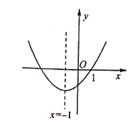
A、1 B、2 C、3 D、47. 如图,抛物线y=ax2+bx+c(a< 0)的图象经过点(1, 2),与x轴交点的横坐标分别为x1 , x2 , 其中-1<x1<0,1<x2<2, 则下列结论中正确的是( )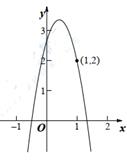 A、a<-1 B、b>2 C、2a+b> 0 D、k为任意实数,关于x的方程ax2 +bx+c+k2 = 0没有实数根8. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。
A、a<-1 B、b>2 C、2a+b> 0 D、k为任意实数,关于x的方程ax2 +bx+c+k2 = 0没有实数根8. 在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:①abc <0;②c+2a<0;③9a-3b+c=0; ④a-b≥m(am+b) (m为实数):⑤4ac-b2<0。其中错误结论的个数有( )
 A、1个 B、2个 C、3个 D、4个9. 如图.抛物线y=ax2+bx+c(a≠0)经过点(-1,0),与y轴交于点(0,2),抛物线的对称轴为直线x=1,下列结论:①a+c=b:②方程ax2+bx+c=0的解为-1和3;③2a+b=0;④abc<0;其中正确的结论有( )
A、1个 B、2个 C、3个 D、4个9. 如图.抛物线y=ax2+bx+c(a≠0)经过点(-1,0),与y轴交于点(0,2),抛物线的对称轴为直线x=1,下列结论:①a+c=b:②方程ax2+bx+c=0的解为-1和3;③2a+b=0;④abc<0;其中正确的结论有( ) A、1个 B、2个 C、3个 D、4个10. 抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( )
A、1个 B、2个 C、3个 D、4个10. 抛物线C1:y1=mx2-4mx+2n-1与平行于x轴的直线交于A、B两点,且A点坐标为(-1,2),请结合图象分析以下结论:①对称轴为直线x=2;②抛物线与y轴交点坐标为(0,-1);③m> ;④若抛物线C2:y2=ax2(a≠0)与线段AB恰有一个公共点,则a的取值范围是 ≤a<2;⑤不等式mx2-4mx+2n>0的解作为函数C1的自变量的取值时,对应的函数值均为正数,其中正确结论的个数有( ) A、2个 B、3个 C、4个 D、5个
A、2个 B、3个 C、4个 D、5个二、填空题
-
11. 在平面直角坐标系xOy中,抛物线y=-x2+6x-8与x轴交于点A , B(点A在点B的左侧),与y轴交于点C . 垂直于y轴的直线l与抛物线交于点P(x1 , y1),Q(x2 , y2),与直线BC交于点N(x3 , y3),若x1<x2<x3 , 记s=x1+x2+x3 , 则s的取值范围为 .12. 如图,抛物线y=﹣x2+bx+c与x轴相交于A、B两点,点A在点B左侧,顶点在折线M﹣P﹣N上移动,它们的坐标分别为M(﹣1,4)、P(3,4)、N(3,1).若在抛物线移动过程中,点A横坐标的最小值为﹣3,则﹣1﹣b+c的最小值是 .
 13. 已知抛物线 的顶点为 ,对称轴 与 轴交于点 , 是 的中点. 在抛物线上, 关于直线 的对称点为 , 关于点 的对称点为 .当 时,线段 的长随 的增大而发生的变化是: . (“变化”是指增减情况及相应 的取值范围)14. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+ x+2和直线y= x-2于点A和点C,以线段AC为对角线作正方形ABCD,则当正方形ABCD的面积最小时m的值为。
13. 已知抛物线 的顶点为 ,对称轴 与 轴交于点 , 是 的中点. 在抛物线上, 关于直线 的对称点为 , 关于点 的对称点为 .当 时,线段 的长随 的增大而发生的变化是: . (“变化”是指增减情况及相应 的取值范围)14. 如图,在平面直角坐标系中,过点P(m,0)作x轴的垂线,分别交抛物线y=x2+ x+2和直线y= x-2于点A和点C,以线段AC为对角线作正方形ABCD,则当正方形ABCD的面积最小时m的值为。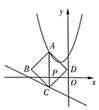 15. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .
15. 如图,抛物线 与 交于点 ,过点 作 轴的平行线,分别交两条抛物线于点 , .则以下结论:①无论 取何值, 2的值总是正数;② ;③当 时, ;④ .其中正确结论是 .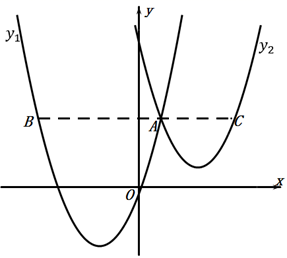 16. 如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1 , 与x轴交于点P1 和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1 , F2 , F3 , …,Fn , 则其中F1的顶点坐标为 , F8的顶点坐标为 , Fn的顶点坐标为(n为正整数,用含n的代数式表示).
16. 如图,在平面直角坐标系xOy中,二次函数y=-x2-2x图象位于x轴上方的部分记作F1 , 与x轴交于点P1 和O;F2与F1关于点O对称,与x轴另一个交点为P2;F3与F2关于点P2对称,与x轴另一个交点为P3;….这样依次得到F1 , F2 , F3 , …,Fn , 则其中F1的顶点坐标为 , F8的顶点坐标为 , Fn的顶点坐标为(n为正整数,用含n的代数式表示). 17. 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是 .
17. 如图,在平面直角坐标系中,线段AB的两个端点的坐标分别为(-1,2)、(1,1).抛物线y=ax2+bx+c(a≠0)与x轴交于C、D两点,点C在点D左侧,当顶点在线段AB上移动时,点C横坐标的最小值为-2.在抛物线移动过程中,a-b+c的最小值是 . 18. 如图,二次函数 的图象与x轴交于A,B两点,与y轴交于点C,点A坐标为 ,点C在 与 之间 不包括这两点 ,抛物线的顶点为D,对称轴为直线 有以下结论:
18. 如图,二次函数 的图象与x轴交于A,B两点,与y轴交于点C,点A坐标为 ,点C在 与 之间 不包括这两点 ,抛物线的顶点为D,对称轴为直线 有以下结论:① ;
②
③ 若点 ,点 是函数图象上的两点,则 ;
④ ;⑤ 可以是等腰直角三角形.
其中正确的结论序号为 .
 19. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②当-1<x<3时,y>0;③a-b+c<0;④3a+c<0.其中正确的是(填序号).
19. 二次函数y=ax2+bx+c(a,b,c是常数,a≠0)图象的对称轴是直线x=1,其图象的一部分如图所示,对于下列说法:①abc<0;②当-1<x<3时,y>0;③a-b+c<0;④3a+c<0.其中正确的是(填序号). 20. 设函数y=x2+2kx+k-1(k为常数),下列说法中:(1)对任意实数k,函数与x轴有两个交点;(2)当x≥-k时,函数y的值都随x的增大而减小;(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上;(4)对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点.正确的说法有(填写序号) .
20. 设函数y=x2+2kx+k-1(k为常数),下列说法中:(1)对任意实数k,函数与x轴有两个交点;(2)当x≥-k时,函数y的值都随x的增大而减小;(3)k取不同的值时,二次函数y的顶点始终在同一条抛物线上;(4)对任意实数k,抛物线y=x2+2kx+k-1都必定经过唯一定点.正确的说法有(填写序号) .三、解答题
-
21. 如图,抛物线 的图象与x轴交于A、B两点(点A在点B的左边),与y轴交于点C,点D为抛物线的顶点.点A坐标的为 ,点C的坐标为 .
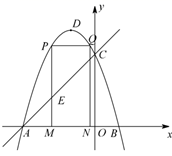 (1)、求抛物线的解析式;(2)、点M为线段 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线 交于点E,与抛物线交于点P,过点P作 交抛物线于点Q,过点Q作 轴于点N.若点P在点Q左边,当矩形 的周长最大时,求 的面积;(3)、在(2)的条件下,当矩形 的周长最大时,连接 ,过抛物线上一点F作y轴的平行线,与直线 交于点G(点G在点F的上方).若 ,求点F的坐标.22. 如图,在平面直角坐标系中,抛物线 经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).
(1)、求抛物线的解析式;(2)、点M为线段 上一点(点M不与点A、B重合),过点M作i轴的垂线,与直线 交于点E,与抛物线交于点P,过点P作 交抛物线于点Q,过点Q作 轴于点N.若点P在点Q左边,当矩形 的周长最大时,求 的面积;(3)、在(2)的条件下,当矩形 的周长最大时,连接 ,过抛物线上一点F作y轴的平行线,与直线 交于点G(点G在点F的上方).若 ,求点F的坐标.22. 如图,在平面直角坐标系中,抛物线 经过原点O,与x轴交于点A(5,0),第一象限的点C(m,4)在抛物线上,y轴上有一点B(0,10).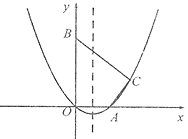
(I)求抛物线的解析式及它的对称轴;
(Ⅱ)点 在线段OB上,点Q在线段BC上,若 ,且 ,求n的值;
(Ⅲ)在抛物线的对称轴上,是否存在点M,使以A,B,M为顶点的三角形是等腰三形?若存在,求出点M的坐标;若不存在,请说明理由.
四、作图题
-
23. 已知抛物线 中(a , b是常数)与y轴的交点为A , 点A与点B关于抛物线的对称轴对称,二次函数 中(b , c是常数)的自变量x与函数值y的部分对应值如下表:,
…
0
1
3
4
…
…
8
0
0
…
(1)、下列结论正确的是A . 抛物线的对称轴是
B . 当 时,y有最大值
C . 当 时,随x的增大而增大
D . 点A的坐标是 ,点B的坐标是
(2)、求二次函数 的解析式(3)、已知点 在抛物线 上,设 的面积为S , 求S与m的函数关系式画出函数图象.并利用函数图象说明S是否存在最大值,为什么?24. 已知y是x的二次函数,该函数的图象经过点A(0,5)、B(1,2)、C(3,2).(1)、求该二次函数的表达式,画出它的大致图象并标注顶点及其坐标;(2)、结合图象,回答下列问题:①当1≤x≤4时,y的取值范围是;
②当m≤x≤m+3时,求y的最大值(用含m的代数式表示);
③是否存在实数m、n(m≠n),使得当m≤x≤n时,m≤y≤n?若存在,请求出m、n;若不存在,请说明理由.
五、综合题
-
25. 疫情期间,某口罩公司销售一种成本为每盒60元的口罩,规定试销期间销售单价不低于成本价,且获利不得高于40%,经试销发现,销售量y(万盒)与销售单价x(元)之间的函数图象如图.
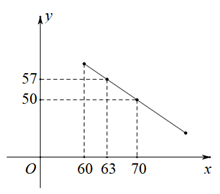 (1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、当售价为元时,销售利润最大,最大利润为万元;(3)、该公司决定每销售一盒口罩,就抽出a(a>0)元钱捐给“火神山”医院,若除去捐款后,所获得的最大利润为756万元,求a的值.26. 某水果连锁店销售热带水果,其进价为20元/千克,销售一段时间后发现:该水果的日销售y(千克)与售价x(元/千克)的函数图象关系 ,设日销售利润为w元.(1)、当日销售利润为1600元时,求售价x值;(2)、当售价为多少元/千克时,当日销售利润w最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了m元/千克 ,物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价的函数关系不变.若日销售最大利润是1280元,请直接写出m的值.27. 在平面直角坐标系xOy中,已知二次函数y=ax2﹣4ax+3a(a≠0)的图象与x轴交于点A , B(A在B的左侧),与y轴交于点C .
(1)、求y与x的函数关系式,并写出自变量x的取值范围;(2)、当售价为元时,销售利润最大,最大利润为万元;(3)、该公司决定每销售一盒口罩,就抽出a(a>0)元钱捐给“火神山”医院,若除去捐款后,所获得的最大利润为756万元,求a的值.26. 某水果连锁店销售热带水果,其进价为20元/千克,销售一段时间后发现:该水果的日销售y(千克)与售价x(元/千克)的函数图象关系 ,设日销售利润为w元.(1)、当日销售利润为1600元时,求售价x值;(2)、当售价为多少元/千克时,当日销售利润w最大,最大利润为多少元?(3)、由于某种原因,该水果进价提高了m元/千克 ,物价局规定该水果的售价不得超过40元/千克,该连锁店在今后的销售中,日销售量与售价的函数关系不变.若日销售最大利润是1280元,请直接写出m的值.27. 在平面直角坐标系xOy中,已知二次函数y=ax2﹣4ax+3a(a≠0)的图象与x轴交于点A , B(A在B的左侧),与y轴交于点C . (1)、直接写出点C的坐标(用含有a的代数式表示);(2)、记△ABC的面积为S , 判断说法:“当a 0时,S与a满足正比例函数关系”的正误,并说明理由;(3)、已知点P(a , 0),Q(0,a﹣3),如果抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.28. 如图,在平面直角坐标系中,抛物线 经过 、 两点,
(1)、直接写出点C的坐标(用含有a的代数式表示);(2)、记△ABC的面积为S , 判断说法:“当a 0时,S与a满足正比例函数关系”的正误,并说明理由;(3)、已知点P(a , 0),Q(0,a﹣3),如果抛物线与线段PQ恰有一个公共点,结合函数图象,求a的取值范围.28. 如图,在平面直角坐标系中,抛物线 经过 、 两点, (1)、求抛物线的解析式及顶点 的坐标;(2)、在二次函数的图象位于 轴上方的部分有两个动点 、 ,且点 在点 的左侧,过点 、 作 轴的垂线,分别交 轴于点 、 .
(1)、求抛物线的解析式及顶点 的坐标;(2)、在二次函数的图象位于 轴上方的部分有两个动点 、 ,且点 在点 的左侧,过点 、 作 轴的垂线,分别交 轴于点 、 .①当四边形 为正方形时,求 的长;
②当四边形 为矩形时,求矩形 周长的最大值
29. 如图1,抛物线y=﹣x2+bx+c经过A(﹣1,0),B(4,0)两点,与y轴相交于点C,连结BC,点P为抛物线上一动点,过点P作x轴的垂线l,交直线BC于点G,交x轴于点E.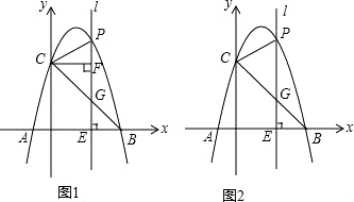 (1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.
(1)、求抛物线的表达式;(2)、当P位于y轴右边的抛物线上运动时,过点C作CF⊥直线l,F为垂足,当点P运动到何处时,以P,C,F为顶点的三角形与△OBC相似?并求出此时点P的坐标;(3)、如图2,当点P在位于直线BC上方的抛物线上运动时,连结PC,PB,请问△PBC的面积S能否取得最大值?若能,请求出最大面积S,并求出此时点P的坐标,若不能,请说明理由.