湘教版备考2021年中考数学二轮复习专题22锐角三角形函数
试卷更新日期:2021-04-27 类型:二轮复习
一、单选题
-
1. 在Rt△ABC中,∠C=90°,AB=26,tanA= ,则AC的长为( )A、25 B、13 C、24 D、122. 一渔船在海岛A南偏东20°方向的B处遇险,测得海岛A与B的距离为20海里,渔船将险情报告给位于A处的救援船后,沿北偏西80°方向向海岛C靠近,同时,从A处出发的救援船沿南偏西10°方向匀速航行,20分钟后,救援船在海岛C处恰好追上渔船,那么救援船航行的速度为( )
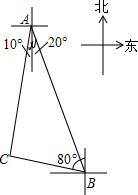 A、 海里/时 B、30海里/时 C、 海里/时 D、 海里/时3. 若规定 ,则sin15°=( )A、 B、 C、 D、4. 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )
A、 海里/时 B、30海里/时 C、 海里/时 D、 海里/时3. 若规定 ,则sin15°=( )A、 B、 C、 D、4. 如图,热气球探测器显示,从热气球A处看一栋楼顶部B处的仰角α为30°,看这栋楼底部C处的俯角β为60°,热气球与楼的水平距离AD为90米,则这栋楼的高度BC为( )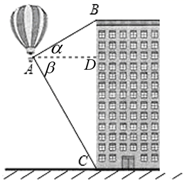 A、 米 B、90 米 C、120 米 D、225米5. 如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , )
A、 米 B、90 米 C、120 米 D、225米5. 如图,小明家附近有一观光塔CD,他发现当光线角度发生变化时,观光塔的影子在地面上的长度也发生变化.经测量发现,当小明站在点A处时,塔顶D的仰角为37°,他继续往前再走5米到达点B(点A,B,C在同一直线上),此时塔顶D的仰角为53°,则观光塔CD的高度约为( )(精确到0.1米,参考数值: , )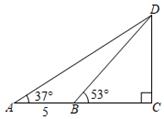 A、7.6米 B、7.8米 C、8.6米 D、8.8米6. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )
A、7.6米 B、7.8米 C、8.6米 D、8.8米6. 如图,一块矩形木板ABCD斜靠在墙边(OC⊥OB,点A,B,C,D,O在同一平面内).已知AB=a,AD=b,∠BCO=x,则点A到OC的距离等于( )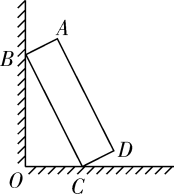 A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx7. 如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )
A、asinx+bsinx B、acosx+bcosx C、asinx+bcosx. D、acosx+bsinx7. 如图,在观测站O处测得船A和灯塔B分别位于正东方向和北偏东60°方向,灯塔B位于船A的北偏东15°方向4海里处,若船A向正东航行,则船A离灯塔B的最近距离是( )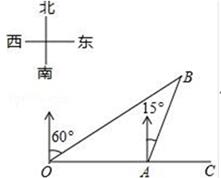 A、( + )海里 B、2 海里 C、( +1)海里 D、2 海里8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里10. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )
A、( + )海里 B、2 海里 C、( +1)海里 D、2 海里8. 在△ABC中,AB=12 ,AC=13,cosB= ,则BC的边长为( )A、7 B、8 C、8或17 D、7或179. 一艘在南北航线上的测量船,于A点处测得海岛B在点A的南偏东30°方向,继续向南航行30海里到达C点时,测得海岛B在C点的北偏东15°方向,那么海岛B离此航线的最近距离是( )(结果保留小数点后两位)(参考数据: )A、4.64海里 B、5.49海里 C、6.12海里 D、6.21海里10. 如图,在△ABC中,∠B=90°,tan∠C= ,AB=6cm.动点P从点A开始沿边AB向点B以1cm/s的速度移动,动点Q从点B开始沿边BC向点C以2cm/s的速度移动.若P,Q两点分别从A,B两点同时出发,在运动过程中,△PBQ的最大面积是( )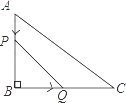 A、18cm2 B、12cm2 C、9cm2 D、3cm2
A、18cm2 B、12cm2 C、9cm2 D、3cm2二、填空题
-
11. 如图,在边长为1的小正方形网格中,点A , B , C , D都在这些小正方形的顶点上,AB , CD相交于点O , 则cos∠BOD= .
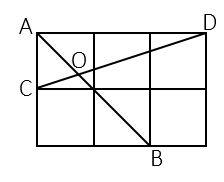 12. 如图,△ABC中,AB=AC=10,tan∠ABC=2,BE⊥AC于点E,D是线段BE上的一个动点,则sin∠ABC = ,CD+ BD的最小值是 .
12. 如图,△ABC中,AB=AC=10,tan∠ABC=2,BE⊥AC于点E,D是线段BE上的一个动点,则sin∠ABC = ,CD+ BD的最小值是 .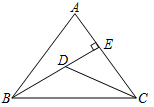 13. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .则观众区的水平宽度 ;顶棚的 处离地面的高度 .( , ,结果精确到 )
13. 某体育看台侧面的示意图如图所示,观众区 的坡度 为 ,顶端 离水平地面 的高度为 ,从顶棚的 处看 处的仰角 ,竖直的立杆上 、 两点间的距离为 , 处到观众区底端 处的水平距离 为 .则观众区的水平宽度 ;顶棚的 处离地面的高度 .( , ,结果精确到 )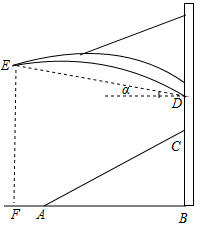 14. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是.
14. 如图, 中, , , 于点D,点E是线段CD的一个动点,则 的最小值是. 15. 如图,在四边形ABCD中,AB= ,AD=7,BC=8,tan ∠B= ,∠C=∠D,则线段CD的长为 .
15. 如图,在四边形ABCD中,AB= ,AD=7,BC=8,tan ∠B= ,∠C=∠D,则线段CD的长为 .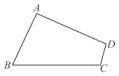 16. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD= .
16. 如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则cos∠AOD= .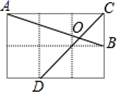 17. 图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,∠E=∠F=90°,两门AB,CD的门轴A,B,C,D都在滑动轨道上.两门关闭时(图2),A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿E→M,F→N的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启。已知AB=50cm,CD=40cm.
17. 图2、图3是某公共汽车双开门的俯视示意图,ME,EF,FN是门轴的滑动轨道,∠E=∠F=90°,两门AB,CD的门轴A,B,C,D都在滑动轨道上.两门关闭时(图2),A,D分别在E,F处,门缝忽略不计(即B,C重合);两门同时开启,A,D分别沿E→M,F→N的方向匀速滑动,带动B,C滑动;B到达E时,C恰好到达F,此时两门完全开启。已知AB=50cm,CD=40cm.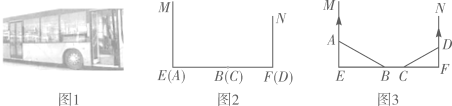 (1)、如图3,当∠ABE=30°时,BC= cm.(2)、在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为cm2 .18. 等腰△ABC的腰AC边上的高BD=3,且CD=5,则tan∠ABD= .19. 在△ABC中,∠C=90°,AC=4,点G为△ABC的重心.如果GC=2,那么sin∠GCB的值是 .20. 在△ABC中,AB=2,AC=3,cos∠ACB= ,则∠ABC的大小为度.
(1)、如图3,当∠ABE=30°时,BC= cm.(2)、在(1)的基础上,当A向M方向继续滑动15cm时,四边形ABCD的面积为cm2 .18. 等腰△ABC的腰AC边上的高BD=3,且CD=5,则tan∠ABD= .19. 在△ABC中,∠C=90°,AC=4,点G为△ABC的重心.如果GC=2,那么sin∠GCB的值是 .20. 在△ABC中,AB=2,AC=3,cos∠ACB= ,则∠ABC的大小为度.三、解答题
-
21. 如图,燕尾槽的横断面是等腰梯形ABCD,现将一根木棒MN放置在该燕尾槽中,木棒与横断面在同一平面内,厚度等不计,它的底端N与点C重合,且经过点A.已知燕尾角∠B=54.5°,外口宽AD=180毫米,木棒与外口的夹角∠MAE=26.5°,求燕尾槽的里口宽BC(精确到1毫米).(参考数据: , , , , , )
 22. 在棚户区改造时,要拆除废旧烟囱 (如图),在烟囱正西方向的楼房 的顶端C处,测得烟囱的顶端A的仰角为 ,底端B的俯角为 已量得 .拆除时若让烟囱向正东方向倒下,试问:距离烟囱正东方向 远的一棵大树是否会被歪倒的烟囱砸到?请说明理由.(参考数据: )
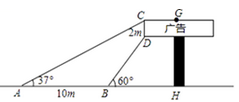
22. 在棚户区改造时,要拆除废旧烟囱 (如图),在烟囱正西方向的楼房 的顶端C处,测得烟囱的顶端A的仰角为 ,底端B的俯角为 已量得 .拆除时若让烟囱向正东方向倒下,试问:距离烟囱正东方向 远的一棵大树是否会被歪倒的烟囱砸到?请说明理由.(参考数据: )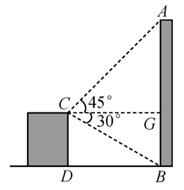 23. 如图,长方形广告牌架在楼房顶部,边长CD=2m,经测量∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.
23. 如图,长方形广告牌架在楼房顶部,边长CD=2m,经测量∠CAH=37°,∠DBH=60°,AB=10m,求GH的长.(参考数据:tan37°≈0.75, ≈1.732,结果精确到0.1m)
四、综合题
-
24. 如图1是某体育看台侧面的示意图,观众区AC的坡度i=1:2,顶端C离水平地面AB的高度为15m,顶棚外沿处的点E恰好在点A的正上方,从D处看E处的仰角α=30°,竖直的立杆上C,D两点间的距离为5m.
 (1)、求观众区的水平宽度AB.(2)、求图1中点E离水平地面的高度EA.(3)、因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)25. 如图所示,在 中, , , , 是边 的中点, 交 于点 .
(1)、求观众区的水平宽度AB.(2)、求图1中点E离水平地面的高度EA.(3)、因为遮阳需要,现将顶棚ED绕D点逆时针转动11°30′,若E点在地面上的铅直投影是点F(图2),求AF.(sin11°30′≈0.20,cos11°30′≈0.98,tan11°30′≈0.20;sin18°30′≈0.32,cos18°30′≈0.95,tan18°30′≈0.33,结果精确到0.1m)25. 如图所示,在 中, , , , 是边 的中点, 交 于点 .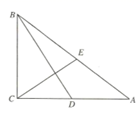 (1)、求 的值;(2)、求 .26. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
(1)、求 的值;(2)、求 .26. 筒车是我国古代利用水力驱动的灌溉工具,唐代陈廷章在《水轮赋》中写道:“水能利物,轮乃曲成”.如图,半径为 的筒车 按逆时针方向每分钟转 圈,筒车与水面分别交于点A、B,筒车的轴心 距离水面的高度 长为 ,简车上均匀分布着若干个盛水筒.若以某个盛水筒 刚浮出水面时开始计算时间.
 (1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )27. 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)
(1)、经过多长时间,盛水筒 首次到达最高点?(2)、浮出水面3.4秒后,盛水筒P距离水面多高?(3)、若接水槽 所在直线是 的切线,且与直线 交于点M, .求盛水筒P从最高点开始,至少经过多长时间恰好在直线 上.(参考数据: , , )27. 如图,某大楼的顶部树有一块广告牌CD,小李在山坡的坡脚A处测得广告牌底部D的仰角为60°.沿坡面AB向上走到B处测得广告牌顶部C的仰角为45°,已知山坡AB的坡度i=1: ,AB=10米,AE=15米.(i=1: 是指坡面的铅直高度BH与水平宽度AH的比)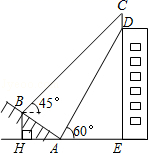 (1)、求点B距水平面AE的高度BH;(2)、求广告牌CD的高度.
(1)、求点B距水平面AE的高度BH;(2)、求广告牌CD的高度.(测角器的高度忽略不计,结果精确到0.1米.参考数据: 1.414,
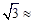 1.732)
1.732)