湘教版备考2021年中考数学二轮复习专题21图形的相似
试卷更新日期:2021-04-27 类型:二轮复习
一、单选题
-
1. 如图,以点O为支点的杠杆,在A端用竖直向上的拉力将重为G的物体匀速拉起,当杠杆OA水平时,拉力为F;当杠杆被拉至OA1时,拉力为F1 , 过点B1作B1C⊥OA,过点A1作A1D⊥OA,垂足分别为点C、D.在下列结论中:
① ;②OA•OC=OB•OD;③OC•G=OD•F1;④F=F1 , 正确的是( )
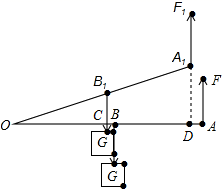 A、①②④ B、②③④ C、①②③ D、①②③④2. 如图,正五边形的边长为2,连接对角线AD、BE、CE , 线段AD分别与BE和CE相交于点M、N , 给出下列结论:①∠AME=108°,②AN2=AM·AD;③MN= ;④BE= ,其中正确的有( )
A、①②④ B、②③④ C、①②③ D、①②③④2. 如图,正五边形的边长为2,连接对角线AD、BE、CE , 线段AD分别与BE和CE相交于点M、N , 给出下列结论:①∠AME=108°,②AN2=AM·AD;③MN= ;④BE= ,其中正确的有( ) A、1个 B、2个 C、3个 D、4个3. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,延长至点G,连接BG,过点A作AF⊥BG,垂足为F,AF交CD于点E,则下列错误的是( )
A、1个 B、2个 C、3个 D、4个3. 如图,在△ABC中,∠ACB=90°,CD⊥AB,垂足为D,延长至点G,连接BG,过点A作AF⊥BG,垂足为F,AF交CD于点E,则下列错误的是( ) A、 B、 C、 D、4. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )
A、 B、 C、 D、4. 将矩形OABC如图放置,O为坐标原点,若点A(﹣1,2),点B的纵坐标是 ,则点C的坐标是( )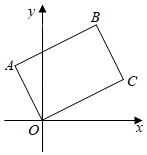 A、(4,2) B、(3, ) C、(3, ) D、(2, )5. 如图,在矩形 中, , 分别为边 , 的中点,线段 , 与对角线 分别交于点 , .设矩形 的面积为 ,则以下4个结论中:① ;② ;③ ;④ .正确的结论有( )
A、(4,2) B、(3, ) C、(3, ) D、(2, )5. 如图,在矩形 中, , 分别为边 , 的中点,线段 , 与对角线 分别交于点 , .设矩形 的面积为 ,则以下4个结论中:① ;② ;③ ;④ .正确的结论有( ) A、1个 B、2个 C、3个 D、4个6. 如图,已知 ,它们依次交直线 、 于点 、 、 和点 、 、 ,如果 , ,那么 等于( )
A、1个 B、2个 C、3个 D、4个6. 如图,已知 ,它们依次交直线 、 于点 、 、 和点 、 、 ,如果 , ,那么 等于( ) A、 B、 C、 D、7. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )
A、 B、 C、 D、7. 在正方形网格中,每个小正方形的顶点称为格点,以格点为顶点的三角形叫做格点三角形.如图,△ABC是格点三角形,在图中的6×6正方形网格中作出格点三角形△ADE(不含△ABC),使得△ADE∽△ABC(同一位置的格点三角形△ADE只算一个),这样的格点三角形一共有( )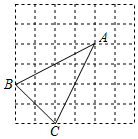 A、4个 B、5个 C、6个 D、7个8. 如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x , 0)且﹣2<x<3,BC⊥AC垂足为点C , 连接AB . 若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )
A、4个 B、5个 C、6个 D、7个8. 如图,已知点A(3,4),点B为直线x=﹣2上的动点,点C(x , 0)且﹣2<x<3,BC⊥AC垂足为点C , 连接AB . 若AB与y轴正半轴的所夹锐角为α,当tanα的值最大时x的值为( )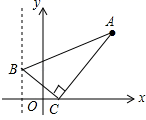 A、 B、 C、1 D、9. 如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为( )
A、 B、 C、1 D、9. 如图,正方形ABCD中,点E为BC右侧一点,∠AEC=90°,作DF⊥AE于点F,若CE=AF=2则正方形的面积为( )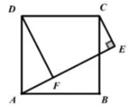 A、16 B、18 C、20 D、2510. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有
A、16 B、18 C、20 D、2510. 如图,M是Rt△ABC的斜边BC上异于B、C的一定点,过M点作直线截△ABC,使截得的三角形与△ABC相似,这样的直线共有 A、1条 B、2条 C、3条 D、4条
A、1条 B、2条 C、3条 D、4条二、填空题
-
11. 如图,在 中, ,点D是 的中点,连结 ,过点B作 ,分别交 于点 ,与过点A且垂直于 的直线相交于点G,连结 ,给出以下几个结论:① ;② ;③点F是 的中点;④ .其中正确的结论是(写出所有正确结论的序号).
 12. 秦九韶的《数书九章》中有一个“峻积验雪”的例子,其原理为:如图,在Rt ABC中,∠C=90°,AC=12,BC=5,AD⊥AB,AD=0.4,过点D作DE AB交CB的延长线于点E,过点B作BF⊥CE交DE于点F,那么BF= .
12. 秦九韶的《数书九章》中有一个“峻积验雪”的例子,其原理为:如图,在Rt ABC中,∠C=90°,AC=12,BC=5,AD⊥AB,AD=0.4,过点D作DE AB交CB的延长线于点E,过点B作BF⊥CE交DE于点F,那么BF= .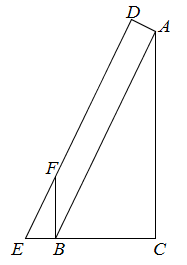 13. 在Rt△ABC中,∠C=90°,AB=13, (如图),将△ABC绕点C旋转后,点A落在斜边AB上的点A’,点B落在点B’,A’B’与边BC相交于点D,那么 的值为 .
13. 在Rt△ABC中,∠C=90°,AB=13, (如图),将△ABC绕点C旋转后,点A落在斜边AB上的点A’,点B落在点B’,A’B’与边BC相交于点D,那么 的值为 .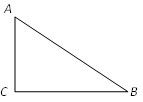 14. 在 中, , , 为边 上的点,联结 (如图所示),如果将 沿直线 翻折后,点 恰好落在边 的中点处,那么点 到 的距离是 .
14. 在 中, , , 为边 上的点,联结 (如图所示),如果将 沿直线 翻折后,点 恰好落在边 的中点处,那么点 到 的距离是 . 15. 若 , 则 的值为 .16. 如图,在 中, .若进行以下操作,在边 上从左到右依次取点 ,过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ,则 .
15. 若 , 则 的值为 .16. 如图,在 中, .若进行以下操作,在边 上从左到右依次取点 ,过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ;过点 作 的平行线分别交 于点 ,则 . 17. 如图,在 中, , 于点 , 于点 .交 于点 ,点 在直线 上运动, , , ,则 的最小值是 .
17. 如图,在 中, , 于点 , 于点 .交 于点 ,点 在直线 上运动, , , ,则 的最小值是 . 18. 如图,在 纸板中,AC=8,BC=4,AB=10,P是AC上一点,过点P沿直线剪下一个与 相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是.
18. 如图,在 纸板中,AC=8,BC=4,AB=10,P是AC上一点,过点P沿直线剪下一个与 相似的小三角形纸板,如果有4种不同的剪法,那么AP长的取值范围是.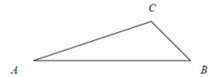 19. 在矩形 中, ,点 在直线 上,且 ,连接 和 交于点 ,若 ,则 的长为 .20. 已知,边长为6的正方形 中, 、 相交于点 ,点 是直线 上一点,点 是直线 上一点,且 ,连接 交 于点 ,交 于点 ,则线段 的长为 .
19. 在矩形 中, ,点 在直线 上,且 ,连接 和 交于点 ,若 ,则 的长为 .20. 已知,边长为6的正方形 中, 、 相交于点 ,点 是直线 上一点,点 是直线 上一点,且 ,连接 交 于点 ,交 于点 ,则线段 的长为 .三、计算题
-
21. 已知xyz≠0且 ,求k的值.
四、解答题
-
22. 如图(图形不全),等边三角形 中, ,点 在直线 上,点 在直线 上,且 ,当 时,求 的长.
几位同学通过探究得出结论:此题有多种结果.有同学已经得出两个符合题意结论:①当点 在边 上、点 在边 上时, ;②当点 在边 上、点 在 的延长线上时, .
要求:请针对其它情况,继续求出 的长,并写出总的正确结论.
 23. 附加题:
23. 附加题:如图,在 中, , ,垂足为 , 、 分别为 、 的中点, ,垂足为 ,求证: .

五、作图题
-
24. 定义:有两个相邻内角互余的凸四边形称为互余四边形,这两个角的夹边称为互余线.
 (1)、在ΔABC中,AB=AC,AD是ΔABC的角平分线,E、F分别是BD,AD上的点,求证:四边形ABEF是互余四边形;(2)、如图2,在5×4的方格纸中,A、B在格点上,请画出一个符合条件的互余四边形ABEF,使AB是互余线,E、F在格点上;(3)、如图3,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF交AC于点N,若N为AC的中点,DE=2BE,如互余线AB=10,求BQ的长.25. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
(1)、在ΔABC中,AB=AC,AD是ΔABC的角平分线,E、F分别是BD,AD上的点,求证:四边形ABEF是互余四边形;(2)、如图2,在5×4的方格纸中,A、B在格点上,请画出一个符合条件的互余四边形ABEF,使AB是互余线,E、F在格点上;(3)、如图3,在(1)的条件下,取EF中点M,连接DM并延长交AB于点Q,延长EF交AC于点N,若N为AC的中点,DE=2BE,如互余线AB=10,求BQ的长.25. 定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”;
理解:
(1)、如图1,△ABC的三个顶点均在正方形网格中的格点上,若四边形ABCD是以AC为“相似对角线”的四边形,请用无刻度的直尺在网格中画出点D(保留画图痕迹,找出3个即可);(2)、如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.请问BD是四边形ABCD的“相似对角线”吗?请说明理由;运用:
(3)、如图3,已知FH是四边形EFGH的“相似对角线”, ∠EFH=∠HFG=30°.连接EG,若△EFG的面积为 ,求FH 的长.26. 如图,矩形ABCD中,AB=4,BC=m(m>1),点E是AD边上一定点,且AE=1. (1)、当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.(2)、如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)(3)、对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?
(1)、当m=3时,AB上存在点F,使△AEF与△BCF相似,求AF的长度.(2)、如图②,当m=3.5时.用直尺和圆规在AB上作出所有使△AEF与△BCF相似的点F.(不写作法,保留作图痕迹)(3)、对于每一个确定的m的值,AB上存在几个点F,使得△AEF与△BCF相似?六、综合题
-
27. 如图1, 是 的高, .
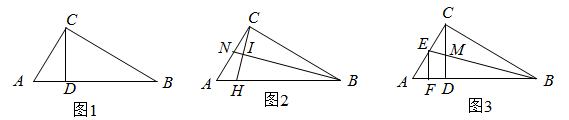 (1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.28. 在梯形 中, , , ,对角线 和 相交于点 ,等腰直角 的直角顶点 与梯形的顶点 重合,将 绕点 旋转
(1)、求证: .(2)、如图2, 是 的中线, 于点I交 于H点,若 ,求 的值.(3)、如图3,M是 的中点, 交 于E, 于F.若 , ,直接写出 的值.28. 在梯形 中, , , ,对角线 和 相交于点 ,等腰直角 的直角顶点 与梯形的顶点 重合,将 绕点 旋转 (1)、如图1,当 的一边 落在 边上,另一边 落在 边的延长线上时,求证:(2)、继续旋转 ,旋转角为 ,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;(3)、如图3,继续旋转 ,当三角形的一边 与梯形对角线 重合, 与 相交于点 时,若 , , ,分别求出线段 、 、 的长.29. 如图1,矩形ABCD中,已知 , ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将 沿直线AE翻折,点B的对应点为点 ,延长 交CD于点M.
(1)、如图1,当 的一边 落在 边上,另一边 落在 边的延长线上时,求证:(2)、继续旋转 ,旋转角为 ,请你在图2中画出图形,并判断(1)中的结论是否成立?若成立加以证明:若不成立,说明理由;(3)、如图3,继续旋转 ,当三角形的一边 与梯形对角线 重合, 与 相交于点 时,若 , , ,分别求出线段 、 、 的长.29. 如图1,矩形ABCD中,已知 , ,点E是线段BC上的一个动点,连接AE并延长,交射线DC于点F.将 沿直线AE翻折,点B的对应点为点 ,延长 交CD于点M.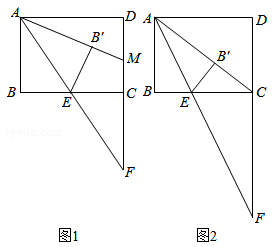 (1)、求证: ;(2)、如图2,若点 恰好落在对角线 上,求 的值.30. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.
(1)、求证: ;(2)、如图2,若点 恰好落在对角线 上,求 的值.30. 如图,平台AB上有一棵直立的大树CD,平台的边缘B处有一棵直立的小树BE,平台边缘B外有一个向下的斜坡BG.小明想利用数学课上学习的知识测量大树CD的高度.一天,他发现大树的影子一部分落在平台CB上,一部分落在斜坡上,而且大树的顶端D与小树顶端E的影子恰好重合,且都落在斜坡上的F处,经测量,CB长5 米,BF长2米,小树BE高1.8米,斜坡BG与平台AB所成的∠ABG=150°.请你帮小明求出大树CD的高度.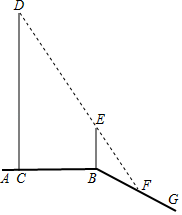
-