湘教版备考2021年中考数学二轮复习专题11一元一次不等式（组）

试卷更新日期：2021-04-27 类型：二轮复习

进入出卷网下载

一、单选题

1. 关于x的不等式 ${\begin{array}{l} x - m > 0 \\ 7 - 2 x > 1 \end{array}$ 的整数解只有4个，则m的取值范围是（）

A、 $- 2 < m \leq - 1$ B、 $- 2 \leq m \leq - 1$ C、 $- 2 \leq m < - 1$ D、 $- 3 < m \leq - 2$

查看试题解析
2. 若关于 x 的不等式组 ${\begin{array}{l} x - 2 < 0 \\ 3 x + 4 > a - x \end{array}$ 恰好只有 2 个整数解，则所有满足条件的整数 a 的值之和是（）

A、3 B、4 C、6 D、1

查看试题解析
3. 老张从一个鱼摊上买了三条鱼，平均每条a元，又从另一个鱼摊上买了两条鱼，平均每条b元，后来他又以每条 $\frac{a + b}{2}$ 元的价格把鱼全部卖给了乙，结果发现赔了钱，原因是（）

A、a＞b B、a＜b C、a＝b D、与a和b的大小无关

查看试题解析
4. 某种出租车的收费标准是：起步价7元(即行驶距离不超过3千米都收7元车费)，超过3千米以后，超过部分每增加1千米，加收2.4元(不足1千米按1千米计)．某人乘这种出租车从甲地到乙地共支付19元，设此人从甲地到乙地经过的路程是x千米，那么x的取值范围是（）

A、1＜x≤11 B、7＜x≤8 C、8＜x≤9 D、7＜x＜8

查看试题解析
5. 运行程序如图所示，从“输入实数 x”到“结果是否＜18”为一次程序操作，若输入 x 后程序操作仅进行了三次就停止，那么 x 的取值范围是（）

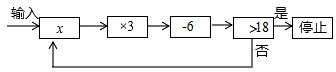A、 $x \geq \frac{32}{9}$ B、 $\frac{32}{9} \leq x \leq \frac{14}{3}$ C、 $\frac{32}{9} < x \leq \frac{14}{3}$ D、 $x \leq \frac{14}{3}$

查看试题解析
6. 设m，n是实数，a，b是正整数，若 $(m + n) a ⩾ (m + n) b$ ，则（）

A、 $m + n + a ⩾ m + n + b$ B、 $m + n - a ⩽ m + n - b$ C、 $\frac{a}{m + n} ⩾ \frac{b}{m + n}$ D、 $\frac{m + n}{a} ⩽ \frac{m + n}{b}$

查看试题解析
7. 不等式组 ${\begin{cases} 3 x + 9 < 5 x + 1 \\ x > 2 m + 2 \end{cases}$ 的解集是x＞4，则m的取值范围是（）

A、m≤2 B、m≥2 C、m≤1 D、m＞1

查看试题解析
8. 已知非负数a,b,c满足条件a+b=7，c-a=5，设S=a+b+c的最大值为m，最小值为n，则m-n的值是（）

A、5 B、6 C、7 D、8

查看试题解析
9. 若不等式组 ${\begin{array}{l} x - a \geq 0, \\ 1 - 2 x > x - 2 \end{array}$ 有解，则a的取值范围是（）

A、a＞－1 B、a≥－1 C、a≤1 D、a＜1

查看试题解析
10. 已知a，b为实数，则解集可以为-2<x<2的不等式组是（）

A、 ${\begin{array}{l} a x > 1 \\ b x > 1 \end{array}$ B、 ${\begin{array}{l} a x > 1 \\ b x < 1 \end{array}$ C、 ${\begin{array}{l} a x < 1 \\ b x > 1 \end{array}$ D、 ${\begin{array}{l} a x < 1 \\ b x < 1 \end{array}$

查看试题解析

二、填空题

11. 任何实数a，可用 $[a]$ 表示不超过a的最大整数，如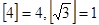，现对72进行如下操作： $72 \overset{第 1 次}{\to} [\sqrt{72}] = 8 \overset{第 2 次}{\to} [\sqrt{8}] = 2 \overset{第 3 次}{\to} [\sqrt{2}] = 1$ ，这样对72只需进行3次操作后变为1，类似地，①对81只需进行次操作后变为1；②只需进行3次操作后变为1的所有正整数中，最大的是.

查看试题解析
12. 若关于x的不等式组 ${\begin{cases} \frac{2 x + 5}{3} > x - 5 \\ \frac{x + 3}{2} < x + a \end{cases}$ 只有5个整数解，则a的取值范围

查看试题解析
13. 已知关于x的不等式组 ${\begin{array}{l} 3 x + m < 0 \\ x > - 5 \end{array}$ 的所有整数解的和为﹣9，m的取值范围为

查看试题解析
14. 邮政部门规定：信函重100克以内（包括100克）每20克贴邮票0.8元，不足20克重以20克计算；超过100克，先贴邮票4元，超过100克部分每100克加贴邮票2元，不足100克重以100克计算．八（9）班有11位同学参加项目化学习知识竞赛，若每份答卷重12克，每个信封重4克，将这11份答卷分装在两个信封中寄出，所贴邮票的总金额最少是元．

查看试题解析
15. 如图，在平面直角坐标系中，点M是直线y=﹣x上的动点，过点M作MN⊥x轴，交直线y=x于点N，当MN≤8时，设点M的横坐标为m，则m的取值范围为．

查看试题解析
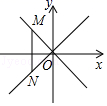16. 已知分式方程 $\frac{2 x + a}{x - 1}$ =1的解为非负数，则a的取值范围是．

查看试题解析
17. 已知关于x的不等式组 ${\begin{array}{l} \frac{2 x + 5}{3} - t > 5 \\ \frac{x + 3}{2} - t > x \end{array}$ 恰有三个整数解，则t的取值范围为.

查看试题解析

三、计算题

18. 解不等式： ||x|-4|+|2x+3|＞8.

查看试题解析
19. 解关于x的不等式组
${\begin{matrix} a (x - 2) > x - 3 \\ 9 (a + 1) x > 9 a x + 8 \end{matrix}$

查看试题解析

四、解答题

20. 已知关于 $x$ 的不等式组 ${\begin{array}{l} 5 x - a > 3 (x - 1) \\ 2 x - 3 \leq 5 \end{array}$ 的所有整数解的和为 $7$ ，求 $a$ 的取值范围

查看试题解析
21. 某单位计划在五一期间组织员工到某地旅游，参加旅游的人数估计为10至25人，甲、乙两家旅行社的服务质量相同，且报价都是每人200元.经过协商，甲旅行社表示可给予每位游客七五折优惠；乙旅行社表示可先免去一位游客的旅游费用，然后给予其余游客八折优惠.该单位选择哪一家旅行社支付的旅游费用较少？

查看试题解析

五、综合题

22. 对于 $x ， y$ 定义一种新运算 $T$ ，规定： $T (x ， y) = a x + 2 b y - 1$ （其中 $a, b$ 均为非零常数），这里等式右边是通常的四则运算，例如：
$T (2, 1) = 2 a + 2 b - 1$

(1)、已知 $T (1, 1) = 3, T (2, - 1) = 1$
①求 $a, b$ 的值；

②若关于 $m$ 的不等式组 ${\begin{array}{l} T (3 m, 2 - m) < 4 \\ T (m, m + 2) > k \end{array}$ 恰好有三个整数解，求实数 $k$ 的取值范围.

(2)、若 $T (x, y) = T (y, x)$ 对于任意不相等的实数 $x, y$ 都成立，求 $a$ 与 $b$ 满足的关系式.

查看试题解析
23. 自学下面材料后，解答问题.
分母中含有未知数的不等式叫分式不等式.如： $\frac{x - 2}{x + 1} > 0$ ； $\frac{2 x + 3}{x - 1} < 0$ 等.那么如何求出它们的解集呢？

根据我们学过的有理数除法法则可知：两数相除，同号得正，异号得负.其字母表达式为：若 $a > 0$ ， $b > 0$ ，则 $\frac{a}{b} > 0$ ；若 $a < 0$ ， $b < 0$ ，则 $\frac{a}{b} > 0$ ；若 $a > 0$ ， $b < 0$ ，则 $\frac{a}{b} < 0$ ；若 $a < 0$ ， $b > 0$ ，则 $\frac{a}{b} < 0$ .

(1)、反之：若 $\frac{a}{b} > 0$ ，则 ${\begin{array}{l} a > 0 \\ b > 0 \end{array}$ 或 ${\begin{array}{l} a < 0 \\ b < 0 \end{array}$ ；若 $\frac{a}{b} < 0$ ，则或.

(2)、根据上述规律，求不等式 $\frac{x - 2}{x + 1} > 0$ 的解集.

(3)、直接写出分式不等式 $\frac{x^{2} + 1}{x - 3} > \frac{x^{2} + 1}{3 x - 2}$ 的解集.

查看试题解析
24. 某公司装修需用A型板材240块、B型板材180块，A型板材规格是60cm×30cm，B型板材规格是40cm×30cm.现只能购得规格是150cm×30cm的标准板材.一张标准板材尽可能多地裁出A型、B型板材，共有下列三种裁法：（如图是裁法一的裁剪示意图）

裁法一
裁法二
裁法三
A型板材块数
1
2
0
B型板材块数
2
m
n
设所购的标准板材全部裁完，其中按裁法一裁x张、按裁法二裁y张、按裁法三裁z张，且所裁出的A、B两种型号的板材刚好够用.

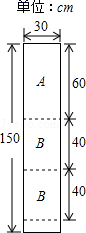(1)、上表中，m= ， n= ；

(2)、分别求出y与x和z与x的函数关系式；

(3)、若用Q表示所购标准板材的张数，求Q与x的函数关系式，并指出当x取何值时Q最小，此时按三种裁法各裁标准板材多少张？

查看试题解析
25. 先阅读理解下面的例题，再按要求解答：
例题：解不等式（x+5）（x-5）>0

解：由有理数的乘法法则“两数相乘，同号得正”，得 ${\begin{cases} x + 5 > 0 \\ x - 5 > 0 \end{cases}$ ①或 ${\begin{cases} x + 5 < 0 \\ x - 5 < 0 \end{cases}$ ②解不等式组①得x>5，解不等式组②得x<-5，

所以不等式的解集为x>5或x<-5。

(1)、求不等式x²-2x-3<0的解集。

(2)、求不等式 $\frac{2 x + 4}{3 x - 1} < 0$ 的解集。

查看试题解析

	裁法一	裁法二	裁法三
A型板材块数	1	2	0
B型板材块数	2	m	n