黑龙江省绥化市2019-2020学年高二下学期理数期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 设集合 $U = {x | 1 \leq x \leq 10 ， x \in Z}$ ， $A = {1 ， 3 ， 5 ， 7 ， 8}$ ， $B = {2 ， 4 ， 6 ， 8}$ ，则 $(∁_{U} A) \cap B =$ （）

A、 ${2 ， 4 ， 6 ， 7}$ B、 ${2 ， 4 ， 5 ， 9}$ C、 ${2 ， 4 ， 6 ， 8}$ D、 ${2 ， 4 ， 6 ，}$

查看试题解析
2. 已知 $z = (1 + i) (2 - i)$ ，则 $| z |^{2} =$ （）

A、 $2 + i$ B、 $3 + i$ C、 $5$ D、 $10$

查看试题解析
3. 函数 $f (x) = \frac{1}{\ln (x + 1)} + \sqrt{4 - x^{2}}$ 的定义域为（）

A、[－2，0)∪(0，2] B、(－1，0)∪(0，2] C、[－2，2] D、(－1，2]

查看试题解析
4. 用数学归纳法证明 $1 + \frac{1}{2} + \frac{1}{3} + \dots + \frac{1}{2^{n} - 1} < n (n \in N^{*} ， n > 1)$ 时，第一步应验证不等式（）

A、 $1 + \frac{1}{2} < 2$ B、 $1 + \frac{1}{2} + \frac{1}{3} < 2$ C、 $1 + \frac{1}{2} + \frac{1}{3} < 3$ D、 $1 + \frac{1}{2} + \frac{1}{3} + \frac{1}{4} < 3$

查看试题解析
5. 已知 $f (x)$ 是偶函数，且在 $(0 ， + \infty)$ 上单调递增，则函数 $f (x)$ 可以是（）

A、 $f (x) = x^{4} - 2 x^{2}$ B、 $f (x) = \frac{e^{x} + e^{- x}}{2}$ C、 $f (x) = x \sin x$ D、 $f (x) = \frac{1}{3} x^{2} + \cos x$

查看试题解析
6. 一件产品要经过2道独立的加工程序，第一道工序的次品率为a ，第二道工序的次品率为b ，则产品的正品率为（）

A、 1－a－b B、1－ab C、(1－a)(1－b) D、1－(1－a)(1－b)

查看试题解析
7. 已知随机变量X服从正态分布 $N (2 ， σ^{2})$ $(σ > 0)$ ，且 $P (X > 0) = 0.9$ ，则 $P (2 < X < 4) =$ （）

A、0.2 B、0.3 C、0.4 D、0.6

查看试题解析
8. 给出下列命题：
①命题“若 $b^{2} - 4 a c < 0$ ，则方程 $a x^{2} + b x + c = 0 (a \neq 0)$ 无实根”的否命题；②命题“在 $Δ A B C$ 中， $A B = B C = C A$ ，那么 $△ A B C$ 为等边三角形”的逆命题；③命题“若 $a > b > 0$ ，则 $\sqrt[3]{a} > \sqrt[3]{b} > 0$ ”的逆否命题；④“若 $m \geq 1$ ，则 $m x^{2} - 2 (m + 1) x + (m + 3) \geq 0$ 的解集为 $R$ ”的逆命题；其中真命题的序号为（）

A、①②③④ B、①②④ C、②④ D、①②③

查看试题解析
9. 已知函数 $f (x) = {\begin{array}{l} 2^{x - 1} - 2 ， x \leq 1 \\ - \log_{2} (x + 1) ， x > 1 \end{array}$ ，且 $f (a) = - 3$ ，则 $f (6 - a) =$ （）

A、 $- \frac{7}{4}$ B、 $- \frac{5}{4}$ C、 $- \frac{3}{4}$ D、 $- \frac{1}{4}$

查看试题解析
10. 已知 $a = 2^{1.2}$ ， $b = {(\frac{1}{2})}^{- 0.8}$ ， $c = \ln 2$ ，则 $a ， b ， c$ 的大小关系为（）

A、 $c < a < b$ B、 $b < c < a$ C、 $b < a < c$ D、 $c < b < a$

查看试题解析
11. 已知x、y的取值如下表所示：
x
0
1
3
4
y
2.2
4.3
4.8
6.7
若从散点图分析，y与x线性相关，且 $\hat{y}$ =0.95x+ $\hat{a}$ ，则 $\hat{a}$ 的值等于（）

A、2.6 B、6.3 C、2 D、4.5

查看试题解析
12. 已知函数 $f(x)$ 的定义域为 $R$ ，且 $f (x) = {\begin{matrix} 2^{- x} - 1 ， x \leq 0 \\ f (x - 1) ， x > 0 \end{matrix}$ ，若方程 $f (x) = x + a$ 有两个不同实根，则 $a$ 的取值范围为（）

A、 $(- \infty ， 1)$ B、 $(- \infty ， 1]$ C、 $(0 ， 1)$ D、 $(- \infty ， + \infty)$

查看试题解析

二、填空题

13. 命题“∃x₀∈R, $4 x_{0}^{2} - a x_{0} + 1 < 0$ ”为假命题，则实数a的取值范围是．

查看试题解析
14. 已知随机变量X的分布列为P(X=i)= $\frac{i}{2 a}$ (i=1，2，3)，则P(X=2)=.

查看试题解析
15. 定义在 $(- 1 ， 1)$ 上的函数 $f (x) = - 3 x - \sin x$ ，如果 $f (1 - a) + f (1 - a^{2}) > 0$ ，则实数 $a$ 的取值范围为.

查看试题解析
16. 点 $P (1 ， 0)$ 到曲线 ${\begin{matrix} x = t^{2} \\ y = 2 t \end{matrix}$ （其中参数 $t \in R$ ）上的点的最短距离为

查看试题解析

三、解答题

17. 已知复数 $z = \frac{1 - 3 i}{1 - i}$ ，求复数 $z$ 在复平面内对应的点，到点 $(- 1 ， 2)$ 的距离.

查看试题解析
18. 在极坐标系中,直线 $l$ 的极坐标方程为 $θ = \frac{π}{3}$ $(ρ \in R)$ ．以极点为原点,极轴为 $x$ 轴的正半轴建立平面直角坐标系,曲线 $C$ 的参数方程为 ${\begin{array}{l} x = 2 \sin α \\ y = 1 - \cos 2 α \end{array}$ ,（ $α$ 为参数）．

(1)、请写出直线 $l$ 的参数方程;

(2)、求直线 $l$ 与曲线 $C$ 交点 $P$ 的直角坐标．

查看试题解析
19. 设甲、乙两位同学上学期间，每天7：30之前到校的概率均为 $\frac{2}{3}$ .假定甲、乙两位同学到校情况互不影响，且任一同学每天到校情况相互独立.
（Ⅰ）用 $X$ 表示甲同学上学期间的三天中7：30之前到校的天数，求随机变量 $X$ 的分布列和数学期望；

（Ⅱ）设 $M$ 为事件“上学期间的三天中，甲同学在7：30之前到校的天数比乙同学在7：30之前到校的天数恰好多2”，求事件 $M$ 发生的概率.

查看试题解析

20. 某公司为了提高某产品的收益，向各地作了广告推广，同时广告对销售收益也有影响，在若干地区各投入4万元广告费用，并将各地区的销售收益绘制成频率分布直方图（如图所示），且拟定一个合理的收益标准

t

（百万元），由于工作人员操作失误，横轴的数据丢失，但可以确定横轴是从0开始计数的.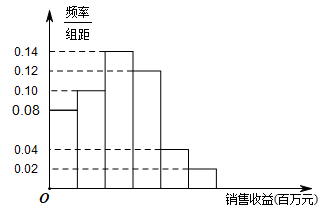

(1)、根据频率分布直方图，计算图中各小长方形的宽度；

(2)、根据频率分布直方图，若该公司想使

74 %

的地区的销售收益超过标准

t

（百万元），估计

t

的值；

(3)、按照类似的研究方法，测得另外一些数据，并整理得到下表：

广告投入 $x$ （单位：万元）	1	2	3	4	5
销售收益 $y$ （单位：百万元）	2	3	2	5	7

表中的数据显示， $x$ 与 $y$ 之间存在线性相关关系，计算 $y$ 关于 $x$ 的回归方程.

（回归直线的斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} x_{i} y_{i} - n \bar{x} \bar{y}}{\sum_{i = 1}^{n} x_{i}^{2} - n {\bar{x}}^{2}}$ ， $\hat{a} = \bar{y} - \hat{b} \bar{x}$ ）

查看试题解析

21. 已知某单位甲、乙、丙三个部门的员工人数分别为24，16，16.现采用分层抽样的方法从中抽取7人，进行睡眠时间的调查.
（I）应从甲、乙、丙三个部门的员工中分别抽取多少人？

（II）若抽出的7人中有4人睡眠不足，3人睡眠充足，现从这7人中随机抽取3人做进一步的身体检查.

（i）用X表示抽取的3人中睡眠不足的员工人数，求随机变量X的分布列与数学期望；

（ii）设A为事件“抽取的3人中，既有睡眠充足的员工，也有睡眠不足的员工”，求事件A发生的概率.

查看试题解析

22. 为了搞好某运动会的接待工作，组委会招募了16名男志愿者和14名女志愿者，调查发现，男、女志愿者中分别有10人和6人喜爱运动，其余人不喜爱运动.

附：

$P (K^{2} \geq k)$	0.050 0.010 0.001
$k$	3.841 6.635 10.828

$K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}$ .

(1)、根据以上数据完成以下

2 \times 2

列联表：

	喜爱运动	不喜爱运动	总计
男	10		16
女	6		14
总计			30

(2)、根据列联表的独立性检验，能否在犯错误的概率不超过0.10的前提下认为性别与喜爱运动有关？

(3)、如果从喜欢运动的女志愿者中（其中恰有4人会外语），抽取2名负责翻译工作，那么抽出的志愿者中至少有1人能胜任翻译工作的概率是多少？

查看试题解析

x	0	1	3	4
y	2.2	4.3	4.8	6.7