河北省邢台市2019-2020学年高二下学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {2, 3, 4, 7}$ ， $B = {x | - 2 x + 7 < 0}$ 则 $A \cap (∁_{R} B) =$ （）

A、 ${3, 4}$ B、 ${2, 3}$ C、 ${2, 3, 4}$ D、 ${3, 4, 7}$

查看试题解析
2. 张先生打算第二天从本地出发到上海，查询得知一天中从本地到上海的动车有4列，飞机有3个航班，且无其他出行方案，则张先生从本地到上海的出行方案共有（）

A、7种 B、12种 C、14种 D、24种

查看试题解析
3. 已知随机变量 $X, Y$ 满足 $Y = a X + b$ ，且 $a, b$ 为正数，若 $D (X) = 2, D (Y) = 8$ ，则（）

A、 $b = 2$ B、 $a = 4$ C、 $a = 2$ D、 $b = 4$

查看试题解析
4. 已知 $a = \log_{3} 4, b = 5^{- 0.5}, c = \log_{3} \frac{1}{2}$ ，则 $a, b, c$ 的大小关系为（）

A、 $c < a < b$ B、 $b < a < c$ C、 $b < c < a$ D、 $c < b < a$

查看试题解析
5. 已知 ${(x^{3} - 2)}^{n}$ 的展开式的所有二项式系数之和为64，则 $n =$ （）

A、9 B、8 C、7 D、6

查看试题解析
6. 函数 $f (x) = \ln x + x - 2$ 的零点所在的大致区间为（）

A、 $(0 ， 1)$ B、 $(1 ， 2)$ C、 $(2 ， e)$ D、 $(e ， 4)$

查看试题解析
7. 已知 ${(\frac{x^{2}}{2} - \frac{1}{\sqrt{x}})}^{n}$ 的展开式中第9项为常数项，则展开式中的各项系数之和为（）

A、 $\frac{1}{2^{10}}$ B、 $- \frac{1}{2^{10}}$ C、 $2^{10}$ D、 $- 2^{10}$

查看试题解析
8. 某同学对如图所示的小方格进行涂色（一种颜色），若要求每行、每列中都恰好只涂一个方格，则不同的涂色种数为（）

A、12 B、36 C、24 D、48

查看试题解析
9. 已知 $η \sim N (1, 4)$ ，若 $P (η > 2 a) = P (η < a - 1)$ ，则 $a =$ （）

A、-1 B、0 C、1 D、2

查看试题解析
10. 函数 $f (x) = (x + \sin x) \cos x$ 的部分图象大致为（）

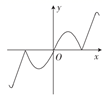A、 B、 C、 D、

查看试题解析
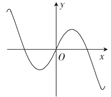11. 已知随机变量X的分布列为

X

0

2

4

P

$\frac{1}{3}$

$\frac{2}{3} - a$

a

则当a在要求范围内增大时，（）

A、 $E (X)$ 增大， $D (X)$ 减小 B、 $E (X)$ 增大， $D (X)$ 增大 C、 $E (X)$ 减小， $D (X)$ 先增大后减小 D、 $E (X)$ 减小， $D (X)$ 先减小后增大

查看试题解析
12. 已知函数 $f (x)$ $(x \in R)$ 满足 $f (x + 2) = f (4 - x)$ ，若函数 $y = x^{2} - 6 x + 1$ 与 $y = f (x)$ 的图象的交点为 $(x_{1}, y_{1}), (x_{2}, y_{2}), (x_{3}, y_{3}), \dots, (x_{n}, y_{n})$ ，则 $x_{1} + x_{2} + x_{3} + \dots + x_{n} =$ （）

A、 $3 n$ B、 $2 n$ C、n D、0

查看试题解析

二、填空题

13. 函数 $f (x)$ 的定义域为R，满足 $f (x) + f (- x) = 0$ ，且当 $x > 0$ 时， $f (x) = x^{2} - 2^{x}$ ，则 $f (- 1) =$ ．

查看试题解析
14. 已知 $C_{n}^{0} 3^{n} + C_{n}^{1} 3^{n - 1} + C_{n}^{2} 3^{n - 2} + \dots + C_{n}^{n - 1} 3 + C_{n}^{n} = 1024$ ，则 $n =$ ．

查看试题解析
15. 已知函数 $f (x) = {\begin{array}{l} \log_{2} (x + 2), x > - 2, \\ x^{2} + 3 x - 2, x ⩽ - 2, \end{array}$ 则 $f (f (- \frac{15}{8})) =$ ．

查看试题解析
16. 十二生肖，又叫属相，是与十二地支相配以人出生年份的十二种动物，包括鼠、牛、虎、兔、龙、蛇、马、羊、猴、鸡、狗、猪，十二生肖的起源与动物崇拜有关．据湖北云梦睡虎地和甘肃天水放马滩出土的秦简可知，先秦时期即有比较完整的生肖系统存在．现有6名学生的属相均是龙、蛇、马中的一个，若每个属相至少有一人，则不同的情况共有种．

查看试题解析

三、解答题

17.

(1)、已知 $f (x)$ 是一次函数，且 $2 f (2 x + 1) - f (x - 2) = 6 x + 5$ ，求 $f (x)$ 的解析式；

(2)、已知函数 $f (x - 3) = x^{2} - 4 x + 6$ ，求 $f (x)$ 的解析式．

查看试题解析

18. 某土特产超市为预估2021年元旦期间游客购买土特产的情况，对2020年元旦期间的购买情况进行随机抽样并统计，得到如下数据：

购买金额（元）	$[0, 15)$	$[15, 30)$	$[30, 45)$	$[45, 60)$	$[60, 75)$	$[75, 90]$
人数	10	15	20	25	20	10

附：参考公式和数据： $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}, n = a + b + c + d$ ．

附表：

$k_{0}$	2.072	2.706	3.841	6.635	7.879
$P (K^{2} ⩾ k_{0})$	0.150	0.100	0.050	0.010	0.005

(1)、估计游客平均购买金额（同一组中的每个数据可用该组区间的中点值代替）；

(2)、根据以上数据完成

2 \times 2

列联表，并判断是否有90%的把握认为购买金额是否少于60元与性别有关．

	不少于60元	少于60	合计
男		40
女	18
合计

查看试题解析

19. 2019年，中华人民共和国成立70周年，为了庆祝建国70周年，某中学在全校进行了一次爱国主义知识竞赛，共1000名学生参加，答对题数（共60题）分布如下表所示：

组别	$[0 ， 10]$	$(10 ， 20]$	$(20 ， 30]$	$(30 ， 40]$	$(40 ， 50]$	$(50 ， 60]$
频数	10	185	265	400	115	25

答对题数 $Y$ 近似服从正态分布 $N (μ ， 81)$ ， $μ$ 为这1000人答对题数的平均值（同一组数据用该组区间的中点值作为代表）.

(1)、估计答对题数在

(12 ， 48]

内的人数（精确到整数位）.

(2)、学校为此次参加竞赛的学生制定如下奖励方案：每名同学可以获得2次抽奖机会，每次抽奖所得奖品的价值与对应的概率如下表所示.

获得奖品的价值（单位：元）	0	10	20
概率	$\frac{3}{10}$	$\frac{1}{2}$	$\frac{1}{5}$

用 $X$ （单位：元）表示学生甲参与抽奖所得奖品的价值，求 $X$ 的分布列及数学期望.

附：若 $Z \sim N (μ ， σ^{2})$ ，则 $\frac{3}{4}$ ， $K^{2} = \frac{n {(a d - b c)}^{2}}{(a + b) (c + d) (a + c) (b + d)}, n = a + b + c + d$ ， $P (μ - 3 σ < Z \leq μ + 3 σ) = 0.9974$ .

查看试题解析

20. 在某公司举行的年会中，为了表彰年度优秀员工，该公司特意设置了一个抽奖环节，其规则如下：一个不透明的箱子中装有形状大小相同的两个红色和四个绿色的小球，从箱子中一次取出两个小球，同色奖励，不同色不奖励，每名优秀员工仅有一次抽奖机会.若取出的两个均为红色，奖励2000元；若两个均为绿色，奖励1000元

(1)、求优秀员工小张获得2000元的概率；

(2)、若一对夫妻均为年度优秀员工，求这对夫妻获得的奖励总金额 $X$ 的分布列和数学期望.

查看试题解析
21. 已知 $m > 0$ ，函数 $f (x) = \lg (2 x - m)$ ．

(1)、当 $m = 1$ 时，解不等式 $f (x) ⩽ 0$ ；

(2)、若对于任意 $t \in [1, \frac{3}{2}], f (x)$ 在区间 $[t, 2 t]$ 上的最大值与最小值的和不大于1，求m的取值范围．

查看试题解析

22. 近年来，我国电子商务快速发展，快递行业的市场规模逐渐扩大．国家邮政局数据显示，2013~2019年，中国快递量持续增长，2019年，我国快递量达到635.2亿件，比前一年增长25.3%，人均使用快递45件左右．某快递公司为预测本公司下一年的快递量，以便提前增加设备和招聘工人，该快递公司对近5年本公司快递量的数据进行对比分析，并对这些数据做了初步处理，得到了下表数据及一些统计量的值，其中

μ_{i} = x_{i}^{2}, v_{i} = \ln y_{i} (i = 1, 2, 3, 4, 5)

．

编号x	1	2	3	4	5
年份	2015	2016	2017	2018	2019
快递量y（单位：百万件）	1	3	6	9	15

$\sum_{i = 1}^{5} {(μ_{i} - \bar{μ})}^{2}$	$\sum_{i = 1}^{5} {(v_{i} - \bar{v})}^{2}$	$\sum_{i = 1}^{5} (μ_{i} - \bar{μ}) (y_{i} - \bar{y})$	$\sum_{i = 1}^{5} (x_{i} - \bar{x}) (v_{i} - \bar{v})$	$\sum_{i = 1}^{5} {(y_{i} - \bar{y})}^{2}$
374	4.4	212	6.5	121

附：①相关系数 $r = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sqrt{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}} \sqrt{\sum_{i = 1}^{n} {(y_{i} - \bar{y})}^{2}}}$ ，回归直线 $\hat{y} = \hat{b} x + \hat{a}$ 中斜率和截距的最小二乘估计公式分别为 $\hat{b} = \frac{\sum_{i = 1}^{n} (x_{i} - \bar{x}) (y_{i} - \bar{y})}{\sum_{i = 1}^{n} {(x_{i} - \bar{x})}^{2}}, \hat{a} = \bar{y} - \hat{b} \bar{x}$ ．

②参考数据： $\sqrt{374} \approx 19.34, \frac{10600}{10637} \approx 0.997, \sqrt{11} \approx 3.3$ ．

(1)、设

{μ_{i}}

和

{y_{i}}

的相关系数为

r_{1}, {x_{i}}

和

{v_{i}}

的相关系数为

r_{2}

，请从相关系数的角度，确定

y = a x^{2} + b

或

y = e^{m x + n}

（其中

a, b, m, n

均为常数，e为自然对数的底数）哪一个拟合程度更好；

(2)、根据（1）的结论及表中数据，建立y关于x的回归方程（系数精确到0.01），并预测2020年度的快递量（单位：百万件，精确到0.01）．

查看试题解析

X	0	2	4
P	$\frac{1}{3}$	$\frac{2}{3} - a$	a