河北省秦皇岛市卢龙县2019-2020学年高二下学期数学期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 已知集合 $A = {x | x > 2}$ ， $B = {x | - 1 \leq x \leq 4}$ ，则 $A \cap B =$ （）

A、 ${x | 2 < x < 4}$ B、 ${x | - 1 < x \leq 2}$ C、 ${x | 2 < x \leq 4}$ D、 ${x | - 1 \leq x \leq 4}$

查看试题解析
2. 已知复数 $z = \frac{1 + a i}{3 + i}$ 为纯虚数（其中i为虚数单位），则实数 $a =$ （）

A、-3 B、3 C、 $- \frac{1}{3}$ D、 $\frac{1}{3}$

查看试题解析
3. 设命题 $p : \forall n \in N, 3^{n} \geq n^{2} + 1$ ,则 $\neg p$ 为（）

A、 $\forall n \in N, 3^{n} < n^{2} + 1$ B、 $\exists n_{0} \in N, 3^{n_{0}} < n_{0}^{2} + 1$ C、 $\forall n \in N, 3^{n} \leq n^{2} + 1$ D、 $\exists n_{0} \in N, 3^{n_{0}} \geq n_{0}^{2} + 1$

查看试题解析
4. 在等差数列 ${a_{n}}$ 中，已知 $a_{1} + a_{5} + a_{9} = 15$ ，则 $a_{4} + a_{6} =$ （）

A、10 B、11 C、12 D、13

查看试题解析
5. 已知 $\vec{a}$ 与 $\vec{b}$ 均为单位向量，若 $\vec{b} ⊥ (2 \vec{a} + \vec{b})$ ，则 $\vec{a}$ 与 $\vec{b}$ 的夹角为（）

A、30° B、45° C、60° D、120°

查看试题解析
6. 双曲线 $\frac{x^{2}}{12} - \frac{y^{2}}{4} = 1$ 的焦点到渐近线的距离为（）

A、 $2 \sqrt{3}$ B、3 C、2 D、 $\sqrt{3}$

查看试题解析
7. 为了得到函数 $y = sin (2 x - \frac{π}{3})$ 的图像，只需把函数 $y = sin (2 x + \frac{π}{6})$ 的图像（）

A、向左平移 $\frac{π}{4}$ 个长度单位 B、向右平移 $\frac{π}{4}$ 个长度单位 C、向左平移 $\frac{π}{2}$ 个长度单位 D、向右平移 $\frac{π}{2}$ 个长度单位

查看试题解析
8. 如图是函数y＝f（x）的导数y＝f'（x）的图象，则下面判断正确的是（）

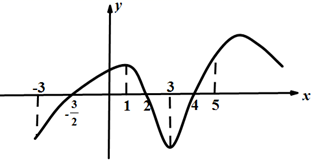A、在（﹣3，1）内f（x）是增函数 B、在x＝1时，f（x）取得极大值 C、在（4，5）内f（x）是增函数 D、在x＝2时，f（x）取得极小值

查看试题解析
9. 定义在 $R$ 上的偶函数 $f (x)$ 满足 $f (x + 2) = f (x)$ ，且在 $[- 1, 0]$ 上单调递减，设 $a = f (- 2.8)$ ， $b = f (- 1.6)$ ， $c = f (0.5)$ ，则 $a$ ， $b$ ， $c$ 大小关系是（）

A、 $a > b > c$ B、 $c > a > b$ C、 $b > c > a$ D、 $a > c > b$

查看试题解析
10. 已知抛物线 $C : y^{2} = 4 x$ 的焦点为 $F$ ，过点 $F$ 的直线与抛物线交于 $A$ ， $B$ 两点，满足 $| A B | = 6$ ，则线段 $A B$ 的中点的横坐标为（）

A、2 B、4 C、5 D、6

查看试题解析
11. 要将甲、乙、丙、丁四位老师分配到 $A 、 B 、 C 、 D$ 四个班级，每个班级一位老师，且甲不能分配到 $A$ 班，则共有分配方案的种数为（）

A、192 B、186 C、24 D、18

查看试题解析
12. 一直三棱柱的每条棱长都是2，且每个顶点都在球 $O$ 的表面上，则球 $O$ 的表面积为（）

A、 $\frac{28}{3} π$ B、 $\frac{\sqrt{22}}{3} π$ C、 $\frac{4 \sqrt{3}}{3} π$ D、 $\sqrt{7} π$

查看试题解析

二、填空题

13. 若直线 $a x - y - 2 = 0$ 与直线 $2 x - (a - 1) y + 1 = 0$ 垂直，则 $a =$ ．

查看试题解析
14. 二项式 ${(1 + 2 x)}^{5}$ 展开式中含 $x^{2}$ 项的系数是（用数字回答）.

查看试题解析
15. 袋中有3个红球，2个白球，现从中取出3个球，则取到的红球个数为2的概率为.

查看试题解析
16. 下列说法正确的是.
①独立性检验中，为了调查变量 $X$ 与变量 $Y$ 的关系，经过计算得到 $P (k^{2} \geq 6.635) = 0.01$ ，表示的意义是有99%的把握认为变量 $X$ 与变量 $Y$ 有关系；

② $f (x) = e^{x} - a x$ 在 $x = 1$ 处取极值，则 $a = e$ ；

③ $a > b$ 是 $\ln a > \ln b$ 成立的充要条件.

查看试题解析

三、解答题

17. 已知函数f（x）＝ $\frac{1}{3} x^{3} - \frac{3}{2} x^{2}$ ﹣4x+1．

(1)、求函数f（x）的单调区间；

(2)、当x∈[﹣2，5]时，求函数f（x）的最大值和最小值．

查看试题解析
18. 在 $Δ A B C$ 中,角 $A$ 、 $B$ 、 $C$ 所对的边分别为 $a$ 、 $b$ 、 $c$ .已知 $a = 2 a \cos A \cos B - 2 b \sin^{2} A$ .

(1)、求 $C$ ；

(2)、若 $Δ A B C$ 的面积为 $\frac{15 \sqrt{3}}{4}$ ，周长为 $15$ ，求 $c$ .

查看试题解析
19. 甲、乙两位同学进行篮球三分球投篮比赛，甲每次投中的概率为 $\frac{1}{3}$ ，乙每次投中的概率为 $\frac{1}{2}$ ，每人分别进行三次投篮．
（I）记甲投中的次数为 $ξ$ ，求 $ξ$ 的分布列及数学期望 $E ξ$ ；

（Ⅱ）求乙至多投中2次的概率；

（Ⅲ）求乙恰好比甲多投进2次的概率．

查看试题解析
20. 如图，在四棱锥 $P - A B C D$ 中，棱 $A B$ ､ $A D$ ､ $A P$ 两两垂直，且长度均为1， $\vec{B C} = \vec{A D}$ .

(1)、求证： $B D ⊥$ 平面 $P A C$ ；

(2)、求直线 $P C$ 与平面 $P B D$ 所成角的正弦值.

查看试题解析
21. 已知点 $F_{1}$ ､ $F_{2}$ 是椭圆 $C : \frac{x^{2}}{a^{2}} + \frac{y^{2}}{b^{2}} = 1 (a > b > 0)$ 的左､右焦点，点 $P$ 是该椭圆上一点，若当 $∠ F_{1} P F_{2} = \frac{π}{3}$ 时， $△ P F_{1} F_{2}$ 面积达到最大，最大值为 $\sqrt{3}$ .

(1)、求椭圆 $C$ 的标准方程；

(2)、设 $O$ 为坐标原点，是否存在过左焦点 $F_{1}$ 的直线 $l$ ，与椭圆交于 $A$ ， $B$ 两点，使得 $△ O A B$ 的面积为 $\frac{12}{13}$ ？若存在，求出直线 $l$ 的方程；若不存在，说明理由.

查看试题解析
22. 已知函数 $f (x) = x^{2} + 2 a \ln x$

(1)、若函数 $f (x)$ 的图象在 $(2 ， f (2))$ 处的切线斜率为1，求实数 $a$ 的值；并求函数 $f (x)$ 的单调区间；

(2)、若函数 $g (x) = \frac{2}{x} + f (x)$ 在 $[1 ， 2]$ 上是减函数，求实数 $a$ 的取值范围.

查看试题解析