福建省三明市2019-2020学年高二下学期数学期末考试试卷
试卷更新日期:2021-04-27 类型:期末考试
一、单选题
-
1. ( )A、 B、 C、 D、2. 某中学共有学生2500人,其中男生1500人,为了解该校学生参加体育锻炼的时间,采用分层抽样的方法从该校全体学生中抽取一个容量为50的样本,则样本中女生的人数为( )A、10 B、15 C、20 D、303. 已知 ,则 ( )A、 B、 C、 D、4. 设 , 满足约束条件 ,则 的最小值为( )A、-1 B、2 C、4 D、55. 如图,将一个正方形平均划分为9个小正方形,去掉中间的小正方形,再对余下的小正方形重复这一操作,得到的图形称为“谢尔宾斯基地毯”.在原正方形内部随机取一点,则该点取自“谢尔宾斯基地毯”的概率是( )
 A、 B、 C、 D、6. 的展开式中常数项是( )A、-252 B、-220 C、220 D、2527. 对于一组具有线性相关关系的数据 ,根据最小二乘法求得回归直线方程为 ,则以下说法正确的是( )A、至少有一个样本点落在回归直线 上 B、预报变量 的值由解释变量 唯一确定 C、相关指数 越小,说明该模型的拟合效果越好 D、在残差图中,残差点分布水平带状区域的宽度越窄,则回归方程的预报精确度越高8. 近几年新能源汽车产业正持续快速发展,动力蓄电池技术是新能源汽车的核心技术.已知某品牌新能源汽车的车载动力蓄电池充放电次数达到800次的概率为 ,充放电次数达到1000次的概率为 .若某用户的该品牌新能源汽车已经经过了800次的充放电,那么他的车能够达到充放电100次的概率为( )A、0.324 B、0.36 C、0.4 D、0.549. 为响应国家“足球进校园”的号召,某校成立了足球队,假设在一次训练中,队员甲有10次的射门机会,且他每次射门踢进球的概率均为0.6,每次射门的结果相互独立,则他最有可能踢进球的个数是( )A、5 B、6 C、7 D、810. 已知函数 的部分图象如图所示,则下列结论正确的是( )
A、 B、 C、 D、6. 的展开式中常数项是( )A、-252 B、-220 C、220 D、2527. 对于一组具有线性相关关系的数据 ,根据最小二乘法求得回归直线方程为 ,则以下说法正确的是( )A、至少有一个样本点落在回归直线 上 B、预报变量 的值由解释变量 唯一确定 C、相关指数 越小,说明该模型的拟合效果越好 D、在残差图中,残差点分布水平带状区域的宽度越窄,则回归方程的预报精确度越高8. 近几年新能源汽车产业正持续快速发展,动力蓄电池技术是新能源汽车的核心技术.已知某品牌新能源汽车的车载动力蓄电池充放电次数达到800次的概率为 ,充放电次数达到1000次的概率为 .若某用户的该品牌新能源汽车已经经过了800次的充放电,那么他的车能够达到充放电100次的概率为( )A、0.324 B、0.36 C、0.4 D、0.549. 为响应国家“足球进校园”的号召,某校成立了足球队,假设在一次训练中,队员甲有10次的射门机会,且他每次射门踢进球的概率均为0.6,每次射门的结果相互独立,则他最有可能踢进球的个数是( )A、5 B、6 C、7 D、810. 已知函数 的部分图象如图所示,则下列结论正确的是( )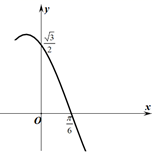 A、 B、 图象关于直线 对称 C、 D、 在 上单调递增
A、 B、 图象关于直线 对称 C、 D、 在 上单调递增二、多选题
-
11. 某教师退休前后各类支出情况如下,已知退休前工资收入为9000元/月,退休后每月储蓄的金额比退休前每月储蓄的金额少1800元,则下面结论中正确的是( )
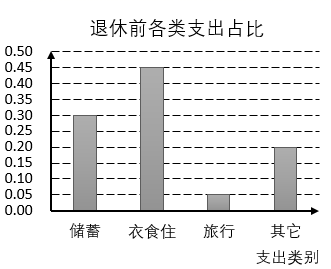

A、该教师退休前每月储蓄支出2700元 B、该教师退休工资收入为6000元/月 C、该教师退休后的旅行支出是退休前旅行支出的3倍 D、该教师退休后的其他支出比退休前的其他支出多12. 已知某三棱锥的三视图如图所示,则下列结论正确的是( )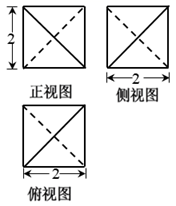 A、该三棱锥的所有棱长都相等 B、该三棱锥的体积为 C、该三棱锥的外接球表面积为 D、该三棱锥内任意一点到各个面的距离之和等于它的高
A、该三棱锥的所有棱长都相等 B、该三棱锥的体积为 C、该三棱锥的外接球表面积为 D、该三棱锥内任意一点到各个面的距离之和等于它的高三、填空题
-
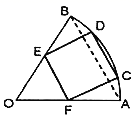
13. 在直角坐标系 中,若角 始边为 轴的非负半轴,终边为射线 : ,则 .14. 某校广播站在下午放学后随机播放歌单收藏的《微微》、《起风了》、《牵丝戏》、《年少有为》4首歌中的2首,则《牵丝戏》、《年少有为》这2首歌中至少有一首被播放的概率为.15. 如图,某公园要在一块圆心角为 ,半径为 的扇形草坪 中修建一个内接矩形文化景观区域 ,若 ,则文化景观区域面积的最大值为 .
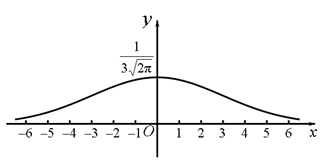
 16. 已知某批零件的长度误差 服从正态分布 ,其密度函数 的曲线如图所示,则 ;从中随机取一件,其长度误差落在 内的概率为.
16. 已知某批零件的长度误差 服从正态分布 ,其密度函数 的曲线如图所示,则 ;从中随机取一件,其长度误差落在 内的概率为.(附:若随机变量 服从正态分布 ,则 , , .)
四、解答题
-
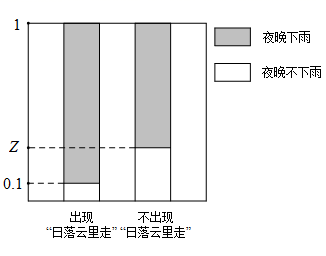
17. 已知 ,且 , .(1)、求 的值;(2)、求 的值.18. “天上钩钩云,地上雨淋淋”,“日落云里走,雨在半夜后”……这些耳熟能详的谚语是千百年来我国劳动人民在生产实践中根据云的形状、走向、速度、厚度、颜色等变化,总结出来的“看云识天气”的宝贵经验.小明同学为了验证“日落云里走,雨在半夜后”的关联性,观察了他所在地区200天“日落云里走”和夜晚天气情况,得到了如图所示 列联表和等高条形图,由于种种原因两图表的信息不全.
夜晚天气
日落云里走
下雨
未下雨
出现
90
未出现
30
附表:
0.10
0.05
0.025
0.010
0.005
0.001
2.706
3.841
5.024
6.635
7.879
10.828
(参考公式 ,其中 )
(1)、根据以上图表的信息,求图表中 , , 的值;(2)、根据以上数据判断能否有99%的把握认为“当晚下雨”与“日落云里走”有关?19. “双十一”是阿里巴巴从2009年起举办的一个全民购物狂欢活动.11年来,天猫“双十一”交易额年年创新高,为预测2020年“双十一”的交易额,收集了历年天猫“双十一”活动的交易额 (亿元),对数据作了初步处理,得到下面的散点图及一些统计量的值.
注:年份代码1-11分别对应年份2009-2019
66
9790
506
152
22
表中 , .
附:对于一组数据 , ,…, ,其回归直线 的斜率和截距的最小二乘估计分别为 , .
(1)、根据散点图判断, 与 哪一个适宜作为交易额 关于时间变量 的回归方程类型?(给出判断即可,不必说明理由)(2)、根据(1)的判断结果及表中数据,建立 关于 的回归方程,并预测2020年“双十一”的交易额.20. 为弘扬我国古代的“六艺”文化,某夏令营主办单位计划利用暑期开设“礼”、“乐”、“射”、“御”、“书”、“数”六门体验课程.(1)、若体验课连续开设六周,每周一门,求其中“射”不排在第一周,“数”不排在最后一周的所有可能排法种数;(2)、甲、乙、丙、丁、戊五名教师在教这六门课程,每名教师至少任教一门课程,求其中甲不任教“数”的课程安排方案种数.21. 已知函数 .(1)、求 的最小正周期;(2)、将 图象上每个点的横坐标变为原来的 倍,再将所得图象向右平移 个长度单位得到 的图象,若 时, 恰有一个零点和两个极值点,求实数 的取值范围.22. 某单位食堂每天以3元/个的价格从面包店购进面包,然后以5元/个的价格出售,如果当天卖不完,剩下的面包以1元/个的价格全部卖给饲料加工厂,根据调查,得到食堂每天面包销售量 (单位:个)的频率分布直方图(如图所示),将频率视为概率,同一组数据用该区间的中点值作为代表. (1)、求面包的日销售量 (单位:个)的分布列和均值;(2)、若食堂每天购买的面包数量相同,该食堂有以下两种购买方案:方案一:按平均数购买;方案二:按中位数购买,请你以利润期望值为决策依据选择更合理的方案.
(1)、求面包的日销售量 (单位:个)的分布列和均值;(2)、若食堂每天购买的面包数量相同,该食堂有以下两种购买方案:方案一:按平均数购买;方案二:按中位数购买,请你以利润期望值为决策依据选择更合理的方案.