北京市朝阳区2019-2020学年度高二下学期数学期末质量检测试卷
试卷更新日期:2021-04-27 类型:期末考试
一、单选题
-
1. 若随机变量X的分布列为
X
0
1
2
P
则X的数学期望 是( )
A、 B、 C、1 D、2. 某物体作直线运动,位移y(单位:m)与时间t(单位:s)满足关系式 ,那么该物体在 s时的瞬时速度是( )A、2m/s B、4m/s C、7m/s D、12m/s3. 曲线 在点 处的切线方程为( )A、 B、 C、 D、4. 的二项展开式中的常数项为( )A、1 B、6 C、15 D、205. 从3名男生和4名女生中各选2人组成一队参加数学建模比赛,则不同的选法种数是( )A、12 B、18 C、35 D、366. 某射手每次射击击中目标的概率都是 ,则这名射手在3次射击中恰有2次击中目标的概率为( )A、 B、 C、 D、7. 曲线 上任意一点P处的切线斜率的取值范围是( )A、 B、 C、 D、8. 一般地,一个程序模块由许多子模块组成,一个程序模块从开始到结束的路线称为该程序模块的执行路径.如图是一个计算机程序模块,则该程序模块的不同的执行路径的条数是( ) A、6 B、14 C、49 D、849. 函数 的图象大致是( )A、
A、6 B、14 C、49 D、849. 函数 的图象大致是( )A、 B、
B、 C、
C、 D、
D、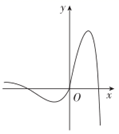 10. 已知函数 , ,若存在 使得 ,则实数a的取值范围是( )A、 B、 C、 D、
10. 已知函数 , ,若存在 使得 ,则实数a的取值范围是( )A、 B、 C、 D、二、填空题
-
11. 已知函数 的导函数为 ,则 .12. 若随机变量 ,则X的数学期望 是.13. 从某校高一年级所有学生中随机选取100名学生,将他们参加知识竞赛的成绩的数据绘制成频率分布直方图,如图所示.从成绩在 , 两组内的学生中,用分层抽样的方法选取了6人参加一项活动,若从这6人中随机选取两人担任正副队长,则这两人来自同一组的概率为.
 14. 某商场举行促销活动,凡购买一定价值的商品便可以获得两次抽奖机会.第一次抽奖中奖的概率是0.5,第二次抽奖中奖的概率是0.3,两次抽奖是否中奖互不影响.那么两次抽奖中至少有一次中奖的概率是.15. 设定义在R上的连续函数 的导函数为 ,已知函数 的图象(如图)与x轴的交点分别为 , , .给出下列四个命题:
14. 某商场举行促销活动,凡购买一定价值的商品便可以获得两次抽奖机会.第一次抽奖中奖的概率是0.5,第二次抽奖中奖的概率是0.3,两次抽奖是否中奖互不影响.那么两次抽奖中至少有一次中奖的概率是.15. 设定义在R上的连续函数 的导函数为 ,已知函数 的图象(如图)与x轴的交点分别为 , , .给出下列四个命题:
①函数 的单调递增区间是 , ;
②函数 的单调递增区间是 , ;
③ 是函数 的极小值点;
④ 是函数 的极小值点.
其中,正确命题的序号是.
16. 在 的二项展开式中,二项式系数之和为;所有项的系数之和为.三、解答题
-
17. 新生婴儿性别比是指在某段时间内新生儿中男婴人数与女婴人数的比值的100倍.下表是通过抽样调查得到的某地区2014年到2018年的年新生婴儿性别比.
年份
2014
2015
2016
2017
2018
新生婴儿性别比
110.8
108.0
106.4
105.4
104.8
(1)、根据样本数据,估计从该地区2015年的新生儿中随机选取1人为女婴的概率(精确到0.01);(2)、从2014年到2018年这五年中,随机选取两年,用X表示该地区的新生婴儿性别比高于107的年数,求X的分布列和数学期望;(3)、根据样本数据,你认为能否否定“生男孩和生女孩是等可能的”这个判断?并说明理由.18. 已知函数 , .(1)、若 ,求证:当 时, 恒成立;(2)、当 时,求 在区间 上的最大值和最小值;(3)、若函数 存在极大值和极小值,且极大值和极小值的差不超过4,求a的取值范围.