河南省郑州市2020届九年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
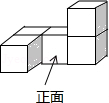
1. 中国人最早使用负数,可追溯到两千多年前的秦汉时期, 的相反数是( )A、 B、 C、 D、2. 如图是一个由5个完全相同的小正方体组成的立体图形,它的俯视图是( )
 A、
A、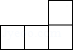 B、
B、 C、
C、 D、
D、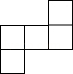 3. 从河南省工商联获悉,自新型冠状病毒引发的肺炎疫情出现以来,截止2月13日下午6点,全省民营企业、商会及企业家个人累计7412家(人),共向武汉等疫情严重地区及我省定点防治新冠肺炎的医院、政府部门、执勤卡点等捐赠物款约10.1亿元.10.1亿用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算正确的是( )A、a4+a2=a6 B、a6÷a2=a3 C、a2•a3=a6 D、(﹣2ab2)3=﹣8a3b65. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF交CD于点G,如果∠2=64°,那么∠1的度数是( )
3. 从河南省工商联获悉,自新型冠状病毒引发的肺炎疫情出现以来,截止2月13日下午6点,全省民营企业、商会及企业家个人累计7412家(人),共向武汉等疫情严重地区及我省定点防治新冠肺炎的医院、政府部门、执勤卡点等捐赠物款约10.1亿元.10.1亿用科学记数法表示应为( )A、 B、 C、 D、4. 下列运算正确的是( )A、a4+a2=a6 B、a6÷a2=a3 C、a2•a3=a6 D、(﹣2ab2)3=﹣8a3b65. 如图,直线AB∥CD,直线EF分别交AB、CD于E、F两点,EG平分∠AEF交CD于点G,如果∠2=64°,那么∠1的度数是( )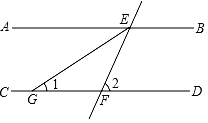 A、24° B、28° C、32° D、36°6. 甲、乙两图分别表示2018年和2019年郑州市财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )
A、24° B、28° C、32° D、36°6. 甲、乙两图分别表示2018年和2019年郑州市财政经费支出情况统计图,阴影部分表示教育经费支出.从中可以看出( )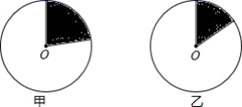 A、2018年教育经费占财政经费支出比例较高 B、2018年教育经费支出金额比较多 C、2018年教育经费支出增幅比较大 D、2018年财政经费支出总额比较小7. 一个盒子里装有两个红球,两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到的球的颜色能配成紫色(红色和蓝色能配成紫色)的概率为( )A、 B、 C、 D、8. 如图,数轴上点A,B分别对应实数1,2,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C,以点A为圆心, 长为半径画弧,交数轴于点M,则点M对应的实数的平方是( )
A、2018年教育经费占财政经费支出比例较高 B、2018年教育经费支出金额比较多 C、2018年教育经费支出增幅比较大 D、2018年财政经费支出总额比较小7. 一个盒子里装有两个红球,两个白球和一个蓝球,这些球除颜色外都相同.从中随机摸出一个球,记下颜色后放回,再从中随机摸出一个球,两次摸到的球的颜色能配成紫色(红色和蓝色能配成紫色)的概率为( )A、 B、 C、 D、8. 如图,数轴上点A,B分别对应实数1,2,过点B作 ,以点B为圆心, 长为半径画弧,交 于点C,以点A为圆心, 长为半径画弧,交数轴于点M,则点M对应的实数的平方是( )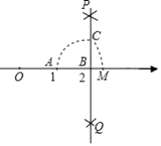 A、2 B、5 C、 D、9. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、10. 如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )
A、2 B、5 C、 D、9. 世界文化遗产“三孔”景区已经完成5G基站布设,“孔夫子家”自此有了5G 网络.5G网络峰值速率为4G 网络峰值速率的10倍,在峰值速率下传输500兆数据,5G 网络比4G 网络快45秒,求这两种网络的峰值速率.设4G网络的峰值速率为每秒传输 兆数据,依题意,可列方程是( )A、 B、 C、 D、10. 如图,Rt△ABC中,AB=4,BC=2,正方形ADEF的边长为2,F、A、B在同一直线上,正方形ADEF向右平移到点F与B重合,点F的平移距离为x,平移过程中两图重叠部分的面积为y,则y与x的关系的函数图象表示正确的是( )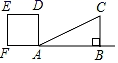 A、
A、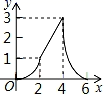 B、
B、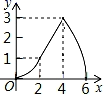 C、
C、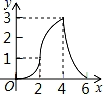 D、
D、
二、填空题
-
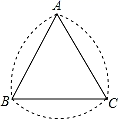
11. 计算: .12. 不等式组 的解集是.13. 乐乐同学的身高为 ,测得他站立在阳光下的影长为 ,紧接着他把手臂竖直举起,测得影长为 ,那么乐乐竖直举起的手臂超出头顶的长度约为 .14. 如图所示的曲边三角形可按下述方法作出:作等边三角形ABC;分别以点A,B,C为圆心,以AB的长为半径作弧BC,AC,AB.三段弧所围成的图形就是一个曲边三角形,如果一个曲边三角形的周长为2π,那么这个曲边三角形的面积是.
 15. 如图,在矩形纸片ABCD中,AB=4,BC=4 ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是.
15. 如图,在矩形纸片ABCD中,AB=4,BC=4 ,点E是AB的中点,点F是AD边上的一个动点,将△AEF沿EF所在直线翻折,得到△A'EF,连接A'C,A'D,则当△A'DC是以A'D为腰的等腰三角形时,FD的长是.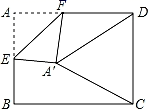
三、解答题
-
16. 先化简,再求值: ,请你选取一个使原分式有意义的a的值代入求值.17. 为迎接2022年冬奥会,鼓励更多的大学生参与到志愿服务中,甲、乙两所学校组织了志愿服务团队选拔活动,经过初选,两所学校各有300名学生进入综合素质展示环节,为了了解这些学生的整体情况,从两校进入综合素质展示环节的学生中分别随机抽取了50名学生的综合素质展示成绩(百分制),并对数据(成绩)进行整理、描述和分析,下面给出了部分信息.
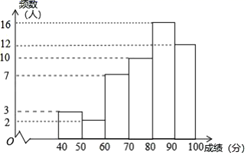
a.甲学校学生成绩的频数分布直方图如图(数据分成6组: , , , , , ).
b.甲学校学生成绩在 这一组是:
80 80 81 81.5 82 83 83 84
85 86 86.5 87 88 88.5 89 89
c.乙学校学生成绩的平均数、中位数、众数、优秀率(85分及以上为优秀)如下:
平均数
中位数
众数
优秀率
83.3
84
78
46%
根据以上信息,回答下列问题:
(1)、甲学校学生A,乙学校学生B的综合素质展示成绩同为82分,这两人在本校学生中综合素质展示排名更靠前的是(填“A”或“B”);(2)、根据上述信息,推断学校综合素质展示的水平更高,理由为:(至少从两个不同的角度说明推断的合理性).(3)、若每所学校综合素质展示的前120名学生将被选入志愿服务团队,预估甲学校分数至少达到分的学生才可以入选.18. 如图,AB是⊙O的直径,BM切⊙O于点B,点P是⊙O上的一个动点(点P不与A,B两点重合),连接AP,过点O作OQ∥AP交BM于点Q,过点P作PE⊥AB于点C,交QO的延长线于点E,连接PQ,OP,AE.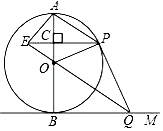 (1)、求证:直线PQ为⊙O的切线;(2)、若直径AB的长为4.
(1)、求证:直线PQ为⊙O的切线;(2)、若直径AB的长为4.①当PE=时,四边形BOPQ为正方形;
②当PE=时,四边形AEOP为菱形.
19. 如图,大楼 高 ,附近有一座塔 ,某人在楼底A处测得塔顶的仰角为 ,爬到楼顶D处测得塔顶的仰角为 分别求塔高 及大楼与塔之间的距离 的长.(结果精确到 ,参考数据: , , , ,)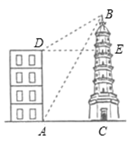 20. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于A,B两点,与x轴相交于点C,连接 ,且 的面积为2.
20. 如图,在平面直角坐标系 中,一次函数 的图象与反比例函数 的图象相交于A,B两点,与x轴相交于点C,连接 ,且 的面积为2.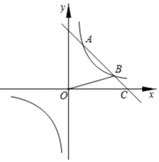 (1)、求反比例函数的表达式;(2)、将直线 向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线 向下平移了几个单位长度?21. 某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.
(1)、求反比例函数的表达式;(2)、将直线 向下平移,若平移后的直线与反比例函数的图象只有一个交点,试说明直线 向下平移了几个单位长度?21. 某单位要印刷“市民文明出行,遵守交通安全”的宣传材料.甲印刷厂提出:每份材料收2元印刷费,另收1000元的制版费;乙印刷厂提出:每份材料收3元印刷费,不收制版费.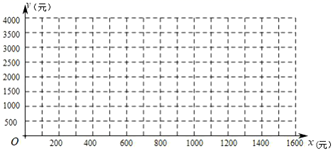 (1)、分别写出两个印刷厂的收费 , (元)与印制数量x(份)之间的关系式(不用写出自变量的取值范围);(2)、在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?(3)、结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?22. 在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:
(1)、分别写出两个印刷厂的收费 , (元)与印制数量x(份)之间的关系式(不用写出自变量的取值范围);(2)、在同一坐标系内画出它们的图象,并求出当印制多少份宣传材料,两个印刷厂的印制费用相同?此时费用为多少?(3)、结合图象回答:在印刷品数量相同的情况下选哪家印刷厂印制省钱?22. 在学习《圆》这一单元时,我们学习了圆周角定理的推论:圆内接四边形的对角互补;事实上,它的逆命题:对角互补的四边形的四个顶点共圆,也是一个真命题.在图形旋转的综合题中经常会出现对角互补的四边形,那么,我们就可以借助“对角互补的四边形的四个顶点共圆”,然后借助圆的相关知识来解决问题,例如:已知: 是等边三角形,点D是 内一点,连接 ,将线段 绕C逆时针旋转 得到线段 ,连接 , , ,并延长 交 于点F.当点D在如图所示的位置时:
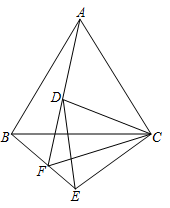 (1)、观察填空:
(1)、观察填空:①与 全等的三角形是;
② 的度数为
(2)、利用题干中的结论,证明:C,D,F,E四点共圆;(3)、直接写出线段 , , 之间的数量关系..23. 如图,抛物线y=﹣ x2+bx+c与x轴交于点A和点B,与y轴交于点C,点B坐标为(4,0),点C坐标为(0,4),点D是抛物线的顶点,过点D作x轴的垂线,垂足为E,连接BD.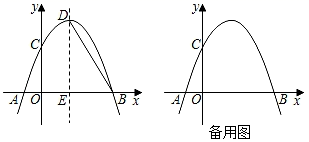 (1)、求抛物线的解析式及点D的坐标;(2)、点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;(3)、若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.
(1)、求抛物线的解析式及点D的坐标;(2)、点F是抛物线上的动点,当∠FBA=2∠BDE时,求点F的坐标;(3)、若点P是x轴上方抛物线上的动点,以PB为边作正方形PBGH,随着点P的运动,正方形的大小、位置也随着改变,当顶点G或H恰好落在y轴上时,请直接写出点P的横坐标.