河南省驻马店市汝南县2020届九年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
1. 下列各数中,比﹣2小的数是( )A、﹣3 B、﹣1 C、0 D、12. 2019年底在武汉发现病毒性肺炎病例,导致春节假期延长,这种致病的新型冠状病毒的直径约为90纳米,1纳米=0.000001毫米,它的直径用科学记数法表示为( )A、 0.9×10-4毫米 B、9×10-5毫米 C、9×10-6毫米 D、9×10-7毫米3. 如图是一个圆柱体切割一部分后的几何体,则其左视图是( )
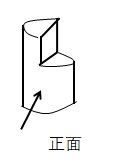 A、
A、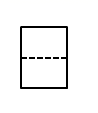 B、
B、 C、
C、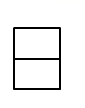 D、
D、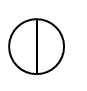 4. 下列各式计算正确的是( )A、 =1 B、a6÷a2=a3 C、x2+x3=x5 D、(﹣x2)3=﹣x65. 某学校对学生的数学成绩按阶段考试、期中考试、期末考试三方面确定最终成绩(考试满分均为 分),若三方面依次按 确定成绩,且张军同学考试后所得的分数依次为 分、 分、 分,则张军同学的最终成绩是( )A、 分 B、 分 C、 分 D、 分6. 如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )
4. 下列各式计算正确的是( )A、 =1 B、a6÷a2=a3 C、x2+x3=x5 D、(﹣x2)3=﹣x65. 某学校对学生的数学成绩按阶段考试、期中考试、期末考试三方面确定最终成绩(考试满分均为 分),若三方面依次按 确定成绩,且张军同学考试后所得的分数依次为 分、 分、 分,则张军同学的最终成绩是( )A、 分 B、 分 C、 分 D、 分6. 如图,在菱形ABCD中,M,N分别在AB,CD上,且AM=CN,MN与AC交于点O,连接BO.若∠DAC=28°,则∠OBC的度数为( )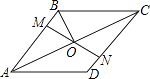 A、28° B、52° C、62° D、72°7. 将抛物线 向左平移 个单位,再向下平移 个单位后得到抛物线 ,则原抛物线是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:
A、28° B、52° C、62° D、72°7. 将抛物线 向左平移 个单位,再向下平移 个单位后得到抛物线 ,则原抛物线是( )A、 B、 C、 D、8. 如图,Rt△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,按下列步骤作图:步骤1:分别以点C和点D为圆心,大于 的长为半径作弧,两弧相交于M,N两点;
步骤2:作直线MN,分别交AC,BC于点E,F;
步骤3:连接DE,DF;
若AC=4,BC=2,则线段DE的长为
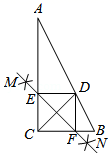 A、 B、 C、 D、9. 如图,在平面直角坐标系中,将正方形 绕点O逆时针旋转 后得到正方形 ,依此方式,绕点O连续旋转 次得到正方 ,如果点A的坐标为 ,那么 的坐标为( )
A、 B、 C、 D、9. 如图,在平面直角坐标系中,将正方形 绕点O逆时针旋转 后得到正方形 ,依此方式,绕点O连续旋转 次得到正方 ,如果点A的坐标为 ,那么 的坐标为( )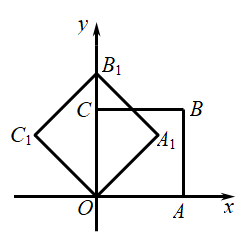 A、 B、 C、 D、10. 如图①, 中,D为 上的动点,D从点A出发以 个单位长度/秒的速度向点B移动, 交折线 于点M,设 , 的面积为y,若y与x的函数图象如图②所示,当M为 中点时,y的值为( )
A、 B、 C、 D、10. 如图①, 中,D为 上的动点,D从点A出发以 个单位长度/秒的速度向点B移动, 交折线 于点M,设 , 的面积为y,若y与x的函数图象如图②所示,当M为 中点时,y的值为( )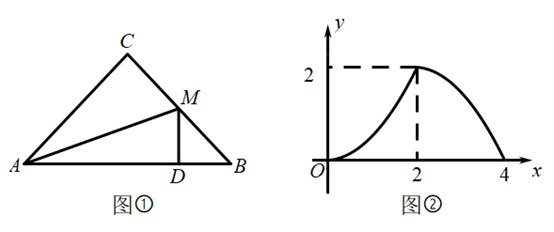 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
11. 计算: .12. 不等式组 的非负整数的解为.13. 某校欲从初三级部3名女生,2名男生中任选两名学生代表学校参加全市举办的“中国梦•青春梦”演讲比赛,则恰好选中一男一女的概率是 .14. 如图,在平面直角坐标系中,已知 经过原点 ,与 轴、 轴分别交于 、 两点,点 坐标为 , 与 交于点 , ,则圆中阴影部分的面积为.
 15. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
15. 在矩形ABCD中,AB=4,BC=3,点P在AB上.若将△DAP沿DP折叠,使点A落在矩形对角线上的A′处,则AP的长为 .
三、解答题
-
16. 先化简: ,再从1,2,3中选取一个适当的数代入求值.17. 万州三中初中数学组深知人生最具好奇心和幻想力、创造力的时期是中学时代,经研究,为我校每一个初中生推荐一本中学生素质数育必读书《数学的奥秘》,这本书就是专门为好奇的中学生准备的.这本书不但给于我们知识,解答生活中的疑惑,更重要的是培养我们细致观察、认真思考、勤于动手的能力.经过一学期的阅读和学习,为了了解学生阅读效果,我们从初一、初二的学生中随机各选20名,对《数学的奥秘》此书阅读效果做测试(此次测试满分:100分).通过测试,我们收集到20名学生得分的数据如下:
初一
96
100
89
95
62
75
93
86
86
93
95
95
88
94
95
68
92
80
78
90
初二
100
98
96
95
94
92
92
92
92
92
86
84
83
82
78
78
74
64
60
92
通过整理,两组数据的平均数、中位数、众数和方差如表:
年级
平均数
中位数
众数
方差
初一
87.5
91
m
96.15
初二
86.2
n
92
113.06
某同学将初一学生得分按分数段( , , , ),绘制成频数分布直方图,初二同学得分绘制成扇形统计图,如图(均不完整),初一学生得分频数分布直方图 初二学生得分扇形统计图(注:x表示学生分数)
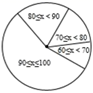
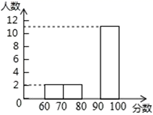
请完成下列问题:
(1)、初一学生得分的众数 ;初二学生得分的中位数 ;(2)、补全频数分布直方图;扇形统计图中, 所对用的圆心角为_▲_度;(3)、经过分析学生得分相对稳定(填“初一”或“初二”);(4)、你认为哪个年级阅读效果更好,请说明理由.18. 如图, 中, ,点O是 边上一点.以O为圆心 长为半径的⊙O与 边相切于D点,与边 相交于点F,连接 交⊙O于点E,连接 .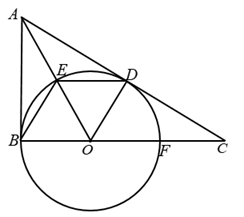 (1)、求证: .(2)、若⊙O的半径为 .
(1)、求证: .(2)、若⊙O的半径为 .①当 的长为时,四边形 为菱形;
②若 .则 的长为.
19. 某商场为方便消费者购物,准备将原来的阶梯式自动扶梯改造成斜坡式自动扶梯,如图所示,已知原阶梯式自动扶梯 长为 ,坡角 为 ”改造后的斜坡式自动扶梯的坡角 为 ,若国标规定自动扶梯的速度一般是 ,请你计算乘坐改造后的斜坡式自动扶梯比乘坐阶梯式自动扶梯多用的时间.(结果保留整数,参考数据: , , .)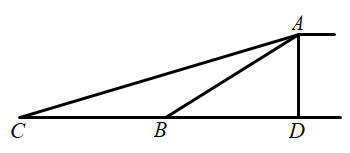 20. 2020 年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和 84 消毒液对校园进行消毒,经调查,若购买 1 箱酒精和 2 箱 84 消毒液共需 210 元,购买 2 箱酒精和 5 箱 84 消毒液共需 500 元.(1)、求酒精和 消毒液的单价;(2)、根据学校实际情况,需从该商店一次性购买酒精和 消毒液共 箱,总费用不超过 元,那么最多可以购买多少箱 消毒液?(3)、由于分阶段开学,九年级学生第一批开学,年级组长张老师准备用 元购买一批酒精和 消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?21. 数学活动课上,张老师引导同学进行如下探究:如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端A固定在桌面上,图2是示意图.
20. 2020 年初,一场突如其来的冠状肺炎肆虐全国,学生经历了“停课不停学”,疫情逐渐消退.某校在开学前夕,准备买一批酒精和 84 消毒液对校园进行消毒,经调查,若购买 1 箱酒精和 2 箱 84 消毒液共需 210 元,购买 2 箱酒精和 5 箱 84 消毒液共需 500 元.(1)、求酒精和 消毒液的单价;(2)、根据学校实际情况,需从该商店一次性购买酒精和 消毒液共 箱,总费用不超过 元,那么最多可以购买多少箱 消毒液?(3)、由于分阶段开学,九年级学生第一批开学,年级组长张老师准备用 元购买一批酒精和 消毒液进行先期消毒,在钱刚好用完的条件下,他有哪几种购买方案?21. 数学活动课上,张老师引导同学进行如下探究:如图1,将长为 的铅笔 斜靠在垂直于水平桌面 的直尺 的边沿上,一端A固定在桌面上,图2是示意图.活动一
如图3,将铅笔 绕端点A顺时针旋转, 与 交于点D,当旋转至水平位置时,铅笔 的中点C与点O重合.
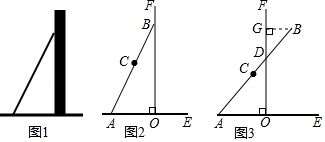 (1)、数学思考
(1)、数学思考设 ,点B到 的距离 .
①用含x的代数式表示: 的长是 , 的长是 ;
②y与x的函数关系式是 , 自变量x的取值范围是.
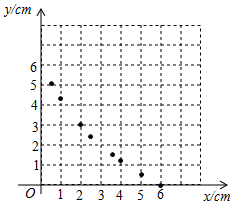
(2)、活动二①列表:根据(1)中所求函数关系式计算并补全表格.
6
5
4
3.5
3
2.5
2
1
0.5
0
0
0.55
1.2
1.58
1.0
2.47
3
4.29
5.08
②描点:根据表中数值,描出①中剩余的两个点 .
③连线:在平面直角坐标系中,请用平滑的曲线画出该函数的图象.
(3)、数学思考请你结合函数的图象,写出该函数的两条性质或结论.
 22.
22.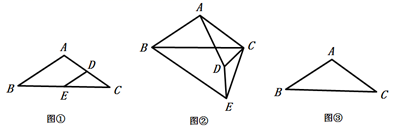 (1)、探索发现
(1)、探索发现如图①,在 中, , , ,点 分别是 的中点,连接,则 的值为.
(2)、拓展探索若将 绕点C逆时针方向旋转一周,在旋转过程中 的值有没有变化?以图②的情形给出证明.
(3)、问题解决如图③,当 旋转到 三点在同一条直线上是,直接写出 的长.
23. 如图1,在平面直角坐标系中,直线y=x+4与抛物线y=﹣ x2+bx+c(b , c是常数)交于A、B两点,点A在x轴上,点B在y轴上.设抛物线与x轴的另一个交点为点C .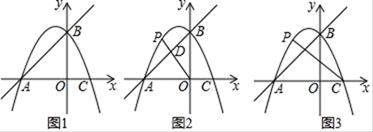 (1)、求该抛物线的解析式;(2)、P是抛物线上一动点(不与点A、B重合),
(1)、求该抛物线的解析式;(2)、P是抛物线上一动点(不与点A、B重合),①如图2,若点P在直线AB上方,连接OP交AB于点D , 求 的最大值;
②如图3,若点P在x轴的上方,连接PC , 以PC为边作正方形CPEF , 随着点P的运动,正方形的大小、位置也随之改变.当顶点E或F恰好落在y轴上,直接写出对应的点P的坐标.