四川省成都市天府新区六校2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 若 $x > y$ ，则下列式子错误的是（）

A、 $x - 3 > y - 3$ B、 $3 - x > 3 - y$ C、 $x + 3 > y + 2$ D、 $\frac{x}{3} > \frac{y}{3}$

查看试题解析
2. 下面的图形中，既是轴对称图形又是中心对称图形的是（）

A、 B、 C、 D、

查看试题解析
3. 要使分式 $\frac{x^{2} - 4}{x - 2}$ 为零，那么x的值是

A、 $- 2$ B、2 C、 $\pm 2$ D、0

查看试题解析
4. 下列从左到右的变形，是分解因式的是（）

A、xy²(x－1)＝x²y²－xy² B、x²＋x－5＝(x－2)(x＋3)＋1 C、(a＋3)(a－3)＝a²－9 D、2a²＋4a＝2a(a＋2)

查看试题解析
5. 不等式 $\frac{1}{4}$ x＞x-1的非负数解的个数是（）

A、1 B、2 C、3 D、无数个

查看试题解析
6. 如图，直线 $y = k x + b$ 与坐标轴的两交点分别为 A(2， 0) 和 B(0，-3) ，则不等式 $k x + b + 3 \leq 0$ 的解为（）

A、 $x \leq 0$ B、 $x \geq 0$ C、 $x \geq 2$ D、 $x < 2$

查看试题解析
7. 下列多项式中不能用公式进行因式分解的是（）

A、a²+a+ $\frac{1}{4}$ B、a²+b²-2ab C、 $- a^{2} + 25 b^{2}$ D、 $- 4 - b^{2}$

查看试题解析
8. 如图所示.在△ABC中，∠C=90°，DE垂直平分AB，交BC于点E，垂足为点D，BE=6cm，∠B=15°，则AC等于（）

A、6cm B、5cm C、4cm D、3cm

查看试题解析
9. 如图，已知正方形ABCD的边长为3，E为CD上一点，DE=1，以点A为中心，把△ADE顺时针旋转90°得△ABE'，连接EE'，则EE'的长度为（）

A、 $2 \sqrt{5}$ B、4 C、3 D、 $5 \sqrt{2}$

查看试题解析
10. 某次自然灾害导致某铁路遂道被严重破坏，为抢修其中一段120米的铁路，施工队每天比原计划多修5米，结果提前4天开通了列车，问原计划每天修多少米？设某原计划每天修x米，所列方程正确的是（）

A、 $\frac{120}{x + 5} - \frac{120}{x} = 4$ B、 $\frac{120}{x} - \frac{120}{x + 5} = 4$ C、 $\frac{120}{x - 5} - \frac{120}{x} = 4$ D、 $\frac{120}{x} - \frac{120}{x - 5} = 4$

查看试题解析

二、填空题

11. 已知 $2 x - y = \frac{1}{3}$ ， $x y = 2$ ，则 $2 x^{2} y - x y^{2} =$ .

查看试题解析
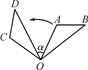
12. 函数y= $\frac{1}{x - 2}$ 中，自变量x的取值范围是．

查看试题解析
13. 如图，将△OAB绕点O逆时针旋转80°，得到△OCD，若∠A=2∠D=100°，则∠α的度数．

查看试题解析
14. 如图，ABCD是一张边长为4cm的正方形纸片，E，F分别为AB，CD的中点，沿过点D的折痕将A 角翻折，使得点A落在EF上的点A′处折痕交AE于点G，则∠ADG=°，EG=cm .

查看试题解析
15. 当k＝时，100x²﹣kxy+49y²是一个完全平方式.

查看试题解析
16. 已知不等式组 ${\begin{matrix} 2 x - a < 1 \\ x - 2 b > 3 \end{matrix}$ 的解集为 $- 1 < x < 1$ ，则 $(a + 1) (b - 1)$ 的值是.

查看试题解析
17. 某商品的标价比成本高 $p %$ ，当该商品降价出售时，为了不亏本，降价幅度不得超过 $d %$ ，若用p表示d，则 $d =$ .

查看试题解析
18. 如图，OA⊥OB，等腰直角△CDE的腰CD在OB上，∠ECD＝45°，将△CDE绕点C逆时针旋转75°，点E的对应点N恰好落在OA上，则 $\frac{O C}{C D}$ 的值为

查看试题解析
19. 如图，把Rt△ABC绕顶点C顺时针旋转90°得到Rt△DFC，若直线DF垂直平分AB，垂足为点E，连接BF，CE，且BC=2.下面四个结论：

①BF= $2 \sqrt{2}$ ；

②∠CBF=45°；

③∠CED=30°；

④△ECD的面积为 $2 \sqrt{2} + 3$ ，

其中正确的结论有.(填番号)

查看试题解析

三、解答题

20.

(1)、解不等式组： ${\begin{matrix} 2 x + 4 \leq 5 (x + 2) \\ x - 1 < \frac{2}{3} x \end{matrix}$ 并把它的解集在数轴上表示出来；

(2)、因式分解： $4 x^{3} - 8 x^{2} + 4 x$ .

查看试题解析
21. 先化简 $(a - 2 + \frac{3}{a + 2}) \div \frac{a^{2} - 2 a + 1}{a + 2}$ ，再从﹣2，0，1中选择一个你喜欢的数代入求值.

查看试题解析
22. 解分式方程： $\frac{x + 1}{x - 1} + \frac{4}{x^{2} - 1} = 1$

查看试题解析
23.
如图，方格纸中的每个小方格都是边长为1个单位长度的正方形，每个小正方形的顶点叫格点，△ABC和△DEF的顶点都在格点上，结合所给的平面直角坐标系解答下列问题：
（1）画出△ABC向上平移4个单位长度后所得到的△A₁B₁C₁；
（2）画出△DEF绕点O按顺时针方向旋转90°后所得到的△D₁E₁F₁；
（3）△A₁B₁C₁和△D₁E₁F₁组成的图形是轴对称图形吗？如果是，请直接写出对称轴所在直线的解析式．

查看试题解析
24. 如图，在△ABC中，∠CAB的平分线AD与BC的垂直平分线DE交于点D，DM⊥AB于M，DN⊥AC的延长线于N.

(1)、求证：BM=CN；

(2)、若AB=8，AC=4，求BM的长.

查看试题解析
25. 如图，等边 $△ A B C$ 中， $A O$ 是 $∠ B A C$ 的角平分线， $D$ 为 $A O$ 上一点，以 $C D$ 为一边且在 $C D$ 下方作等边 $△ C D E$ ，连接 $B E$ ．

(1)、求证： $△ A C D$ ≌ $△ B C E$ ．

(2)、延长 $B E$ 至 $Q$ ， $P$ 为 $B Q$ 上一点，连接 $C P$ 、 $C Q$ 使 $C P = C Q = 5$ ，若 $B C = 6$ ，求 $P Q$ 的长．

查看试题解析
26. 已知关于x、y的方程组 ${\begin{matrix} x + 2 y = 1 \\ x - 2 y = m \end{matrix}$ 的解都小于1，若关于a的不等式组 ${\begin{matrix} \frac{1}{5} a + 2 \geq 1 \\ 2 n - 3 a \geq 1 \end{matrix}$ 恰好有三个整数解.

(1)、分别求出m与n的取值范围；

(2)、化简： $| m + 3 | - \sqrt{1 - 2 m + m^{2}} + | 2 n + 8 |$

查看试题解析
27. 为了迎接“十•一”小长假的购物高峰.某运动品牌专卖店准备购进甲、乙两种运动鞋.其中甲、乙两种运动鞋的进价和售价如下表：

运动鞋

价格

甲

乙

进价（元/双）

m

m﹣20

售价（元/双）

240

160

已知：用3000元购进甲种运动鞋的数量与用2400元购进乙种运动鞋的数量相同.

(1)、求m的值；

(2)、要使购进的甲、乙两种运动鞋共200双的总利润（利润=售价﹣进价）不少于21700元，且不超过22300元，问该专卖店有几种进货方案？

(3)、在（2）的条件下，专卖店准备对甲种运动鞋进行优惠促销活动，决定对甲种运动鞋每双优惠a（50＜a＜70）元出售，乙种运动鞋价格不变.那么该专卖店要获得最大利润应如何进货？

查看试题解析
28. 图1，在平面直角坐标系xOy中，直线l₁ ， l₂都经过点A(﹣6，0)，它们与y轴的正半轴分别相交于点B，C，且∠BAO=∠ACO=30 $°$

(1)、求直线l₁ ， l₂的函数表达式；

(2)、设P是第一象限内直线l₁上一点，连接PC，有S_△ACP=24 $\sqrt{3}$ .M，N分别是直线l₁ ， l₂上的动点，连接CM，MN，MP，求CM+MN+NP的最小值；

(3)、如图2，在(2)的条件下，将△ACP沿射线PA方向平移，记平移后的三角形为△A′C′P′，在平移过程中，若以A，C'，P为顶点的三角形是等腰三角形，请直接写出所有满足条件的点C′的坐标.

查看试题解析