陕西省渭南市2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
1. 下列不等式中,属于一元一次不等式的是( )A、4>1 B、3x–2<4 C、 <2 D、4x–3<2y–72. 在△ABC中,已知CA=CB,∠A=45°,BC=5,则AB的长为( )A、 B、 C、5 D、23. 不等式 的解集在数轴上表示为( )A、
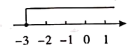 B、
B、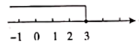 C、
C、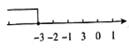 D、
D、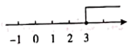 4. 到三角形三个顶点距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点5. 等腰三角形的一个角是40°,则它的底角是( )A、40° B、40°或70° C、80°或70° D、70°6. 如果 ,那么下列不等式中正确的是( )A、 B、 C、 D、7. 下列命题的逆命题是假命题的是( )A、同旁内角互补,两直线平行 B、偶数一定能被 整除 C、如果两个角是直角,那么这两个角相等 D、如果一个数能被 整除,那么这个数也能被 整除8. 如图,点D、E分别在△ABC的边AC、BC上,且DE垂直平分AC,若△ABE的周长为13,AD=5,则△ABC的周长是( )
4. 到三角形三个顶点距离相等的点是( )A、三条角平分线的交点 B、三边中线的交点 C、三边上高所在直线的交点 D、三边的垂直平分线的交点5. 等腰三角形的一个角是40°,则它的底角是( )A、40° B、40°或70° C、80°或70° D、70°6. 如果 ,那么下列不等式中正确的是( )A、 B、 C、 D、7. 下列命题的逆命题是假命题的是( )A、同旁内角互补,两直线平行 B、偶数一定能被 整除 C、如果两个角是直角,那么这两个角相等 D、如果一个数能被 整除,那么这个数也能被 整除8. 如图,点D、E分别在△ABC的边AC、BC上,且DE垂直平分AC,若△ABE的周长为13,AD=5,则△ABC的周长是( ) A、18 B、23 C、21 D、269. 对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=11.请根据上述的定义解决问题:若不等式2※x>2,则不等式的解为( )A、x>1 B、x>2 C、x<1 D、x<210. 如图,△ABC是等边三角形,AB=12,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF的长是( )
A、18 B、23 C、21 D、269. 对于任意实数a、b,定义一种运算:a※b=ab﹣a+b﹣2.例如,2※5=2×5﹣2+5﹣2=11.请根据上述的定义解决问题:若不等式2※x>2,则不等式的解为( )A、x>1 B、x>2 C、x<1 D、x<210. 如图,△ABC是等边三角形,AB=12,点D是BC边上任意一点,DE⊥AB于点E,DF⊥AC于点F,则BE+CF的长是( ) A、6 B、5 C、12 D、8
A、6 B、5 C、12 D、8二、填空题
-
11. 将不等式“ ”化为“ ”的形式为:.12. 在△ABC中,若∠C=90°,∠B=30°,BC=5,则AB的长为.(结果保留根号)13. 如图,已知OA=OB=OC,BC∥AO,若∠A=36°,则∠B的度数为.
 14. 一个篮球队共打了12场比赛,其中赢的场数比平的场数要多,平的场数比输的场数要多,则这个篮球队赢了的场数最少为.
14. 一个篮球队共打了12场比赛,其中赢的场数比平的场数要多,平的场数比输的场数要多,则这个篮球队赢了的场数最少为.三、解答题
-
15. 解不等式:1﹣3(x﹣1)<8﹣x.16. 已知:线段AB和AB外一点C.
求作:AB的垂线,使它经过点C(要求:尺规作图,保留作图痕迹,不写作法).
 17.
17.已知:如图,△ABO是等边三角形,CD∥AB,分别交AO、BO的延长线于点C、D.求证:△OCD是等边三角形.
 18. 用反证法求证:三角形的一个外角等于与它不相邻的两个内角的和.
18. 用反证法求证:三角形的一个外角等于与它不相邻的两个内角的和.已知:如图,∠1是△ABC的一个外角.

求证:∠1=∠A+∠B.
19. 已知关于x的方程4(x+2)-5=3a+2的解不大于 ,求字母a的取值范围20. 如图,在△ABC中,∠ACB=90°,D为AB边上的一点,∠BCD=∠A=30°,BC=4cm,求AD的长. 21. 已知x是1+ ≥2﹣ 的一个负整数解,请求出代数式(x+1)2﹣4x的值.22. 如图,四边形ABCD中,∠BCD=90°,AD⊥DB,DE=BE,BD平分∠ABC,连接EC,若∠A=30°,DB=4,求EC的长.
21. 已知x是1+ ≥2﹣ 的一个负整数解,请求出代数式(x+1)2﹣4x的值.22. 如图,四边形ABCD中,∠BCD=90°,AD⊥DB,DE=BE,BD平分∠ABC,连接EC,若∠A=30°,DB=4,求EC的长. 23. 如图,△ABC中,AB=AC , D为BC边的中点,DE⊥AB .
23. 如图,△ABC中,AB=AC , D为BC边的中点,DE⊥AB .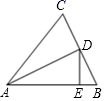 (1)、求证:∠BAC=2∠EDB;(2)、若AC=6,DE=2,求△ABC的面积.
(1)、求证:∠BAC=2∠EDB;(2)、若AC=6,DE=2,求△ABC的面积.
