安徽省宣城市2019-2020学年高二下学期理数期末考试试卷

试卷更新日期：2021-04-27 类型：期末考试

进入出卷网下载

一、单选题

1. 从某校高二1000名学生中采用等距离系统抽样的方法抽取10名学生作代表，学生的编号从000到999，若第一组中抽到的号码是003，则第三组中抽到的号码是（）

A、023 B、033 C、203 D、303

查看试题解析
2. 甲、乙两名篮球运动员10场比赛得分的茎叶图如图所示，则甲、乙两名运动员得分数据的中位数之差的绝对值是（）

A、0 B、1 C、2 D、3

查看试题解析
3. 已知一组数据（1，2），（3，5），（6，8）， $(x_{0}, y_{0})$ 的线性回归方程为 $\overset{\land}{y} = x + 2$ ，则 $x_{0} - y_{0}$ 的值为（）

A、-3 B、-5 C、-2 D、-1

查看试题解析
4. 从装有2个红球和2个白球的口袋内任取2个球，互斥而不对立的两个事件是（）

A、至少有1个白球；都是白球 B、至少有1个白球；至少有1个红球 C、恰有1个白球；恰有2个白球 D、至少有1个白球；都是红球

查看试题解析

5. 《周易》历来被人们视为儒家经典之首，它表现了古代中华民族对万事万物的深刻而又朴素的认识，是中华人文文化的基础，它反映了中国古代的二进制计数的思想方法.我们用近代术语解释为：把阳爻“

”当做数字“1”，把阴爻“

”当做数字“0”，则八卦代表的数表示如下：

卦名	符号	表示的二进制数	表示的十进制数
坤		000	0
震		001	1
坎		010	2
兑		011	3

以此类推，则六十四卦中的“益”卦，符号“ ”表示的十进制数是（）

A、49 B、50 C、81 D、97

查看试题解析

6. 甲在微信群中发布6元“拼手气”红包一个，被乙、丙、丁三人抢完．若三人均领到整数元，且每人至少领到1元，则乙获得“最佳手气”(即乙领取的钱数不少于其他任何人)的概率是（）

A、 $\frac{3}{4}$ B、 $\frac{1}{3}$ C、 $\frac{3}{10}$ D、 $\frac{2}{5}$

查看试题解析
7. 某程序框图如图所示，若该程序运行后输出的值是 $\frac{15}{8}$ ，则m的整数值为（）

A、6 B、7 C、8 D、9

查看试题解析
8. 不等式 $x^{2} - x - 2 < 0$ 成立的一个充分不必要条件是 $a < x < a^{2} + 1$ ，则 $a$ 的取值范围为（）

A、 $- 1 \leq a \leq 1$ B、 $- 1 \leq a < 1$ C、 $- 1 < a < 1$ D、 $- 1 < a \leq 1$

查看试题解析
9. 已知点 $F_{1}$ ， $F_{2}$ 分别是椭圆 $C_{1}$ 和双曲线 $C_{2}$ 的公共焦点， $e_{1}$ ， $e_{2}$ 分别是 $C_{1}$ 和 $C_{2}$ 的离心率，点P为 $C_{1}$ 和 $C_{2}$ 的一个公共点，且 $∠ F_{1} P F_{2} = \frac{2 π}{3}$ ，若 $e_{2} = 2$ ，则 $e_{1}$ 的值是（）

A、 $\frac{\sqrt{5}}{5}$ B、 $\frac{\sqrt{5}}{4}$ C、 $\frac{2 \sqrt{5}}{7}$ D、 $\frac{2 \sqrt{5}}{5}$

查看试题解析
10. 已知函数 $f (x) = x + \frac{4}{x}$ ， $g (x) = 2^{x} + a$ ，若 $\forall x_{1} \in [\frac{1}{2} ， 1]$ ， $\exists x_{2} \in [2 ， 3]$ ， $f (x_{1}) \geq g (x_{2})$ 恒成立，则实数a的取值范围是（）

A、 $a \leq 1$ B、 $a \leq 0$ C、 $a \leq - \frac{1}{2}$ D、 $a \leq - 4$

查看试题解析
11. 若120°的二面角 $α - l - β$ 的棱l上有A ， B两点，AC ， BD分别在半平面α ， β内， $A C ⊥ l$ ， $B D ⊥ l$ ，且 $A B = A C = B D = 1$ ，则CD的长等于（）

A、 $\sqrt{5}$ B、2 C、 $\sqrt{3}$ D、 $\sqrt{2}$

查看试题解析
12. 已知 $F_{1}$ 、 $F_{2}$ 是双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{b^{2}} = 1 (a > 0 ， b > 0)$ 的左、右焦点，过点 $F_{1}$ 作直线 $l$ 与圆 $x^{2} + y^{2} = a^{2}$ 相切于点 $A$ ，且与双曲线的右支相交于点 $B$ ，若 $A$ 是 $B F_{1}$ 上的一个靠近点 $F_{1}$ 的三等分点，且 $| B F_{2} | = 10$ ，则该双曲线方程为（）

A、 $\frac{x^{2}}{4} - \frac{y^{2}}{6} = 1$ B、 $\frac{x^{2}}{16} - \frac{y^{2}}{10} = 1$ C、 $\frac{x^{2}}{16} - \frac{y^{2}}{36} = 1$ D、 $\frac{x^{2}}{36} - \frac{y^{2}}{64} = 1$

查看试题解析

二、填空题

13. 命题“对任意 $x \in R$ ，都有 $2^{x} \leq x$ ”的否定是.

查看试题解析
14. 如图风筝图案中的大、小三角形分别为全等的等腰直角三角形，向图中任意投掷一飞镖，则飞镖落在阴影部分的概率为.

查看试题解析
15. 双曲线 $C ： \frac{x^{2}}{a^{2}} - \frac{y^{2}}{3} = 1 (a > 0)$ 的一条渐近线的倾斜角为60°， $F_{1}$ 、 $F_{2}$ 为左、右焦点，若直线 $x = 2$ 与双曲线 $C$ 交于点 $P$ ，则 $△ P F_{1} F_{2}$ 的周长为.

查看试题解析
16. 过抛物线 $y^{2} = 2 p x (p > 0)$ 的焦点作倾斜角为 $45 °$ 的直线与该抛物线交于P ， Q两点，P ， Q在x轴上的射影分别为R ， S.若梯形PRQS的面积为12，则 $p$ 的值为.

查看试题解析

三、解答题

17. 已知命题p：方程 $\frac{x^{2}}{m + 2} + \frac{y^{2}}{1 - m} = 1$ 表示焦点在y轴上的双曲线；命题q：不等式 $4 x^{2} > 4 (m + 2) x - 1$ 恒成立.若 $p \lor q$ 为真， $p \land q$ 为假，求实数m的取值范围.

查看试题解析
18. 某校从参加某次知识竞赛的1000同学中，随机抽取60名同学将其成绩（百分制，均为整数）分成 $[40 ， 50)$ ， $[50 ， 60)$ ， $[60 ， 70)$ ， $[70 ， 80)$ ， $[80 ， 90)$ ， $[90 ， 100]$ 六组后，得到部分频率分布直方图（如图），观察图形中的信息，回答下列问题：

(1)、补全频率分布直方图，并估计本次知识竞赛的均分；

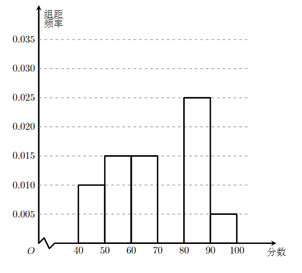(2)、如果确定不低于85分的同学进入复赛，问这1000名参赛同学中估计有多少人进人复赛；

(3)、若从第一组，第二组和第六组三组学生中分层抽取6人，再从这6人中随机抽取2人，求所抽取的2人成绩之差的绝对值大于20的概率.

查看试题解析
19. 如图，直三棱柱 $A B C - A_{1} B_{1} C_{1}$ 中，D是棱 $A A_{1}$ 的中点，且 $A C = B C = \frac{1}{2} A A_{1} = 2$ ， $B D = 2 \sqrt{3}$ .

（Ⅰ）证明：平面 $B C D ⊥$ 平面 $A C C_{1} A_{1}$ ；

（Ⅱ）求二面角 $A - B D - C_{1}$ 的大小.

查看试题解析
20. 如图，已知圆 $E ： {(x + \sqrt{3})}^{2} + y^{2} = 16$ ，点P是圆E上任意一点，且 $F (\sqrt{3} ， 0)$ ，线段PF的垂直平分线与半径PE相交于点Q.

（Ⅰ）求动点Q的轨迹Γ方程；

（Ⅱ）已知A ， B ， C是轨迹Γ的三个动点，A与B关于原点对称，且 $| C A | = | C B |$ ，当△ $A B C$ 的面积为 $\frac{8}{5}$ 时，求点C的坐标.

查看试题解析
21. 如图1，梯形ABCD中， $A B || C D$ ，过 $A$ ， $B$ 分别作 $A E ⊥ C D$ ， $B F ⊥ C D$ ，垂足分别为E.F.若 $A B = A E = 2$ ， $C D = 5$ ， $D E = 1$ ，将梯形 $A B C D$ 沿 $A E$ ， $B F$ 折起，且平面 $A D E ⊥$ 平面 $A B F E$ （如图2）.

（Ⅰ）证明： $A F ⊥ B D$ ；

（Ⅱ）若 $C F || D E$ ，在线段 $A B$ 上是否存在一点 $P$ ，使得直线 $C P$ 与平面 $A C D$ 所成角的正弦值为 $\frac{\sqrt{6}}{18}$ ，若存在，求出 $A P$ 的值，若不存在，说明理由.

查看试题解析
22. 已知抛物线 $C$ 的顶点为坐标原点，准线方程为 $x = - 1$ ，过焦点F的直线l与抛物线C相交于 $A ， B$ 两点，线段 $A B$ 的中点为 $M$ ，且 $k_{O M} = \frac{\sqrt{2}}{2}$ .
（Ⅰ）求直线l的方程；

（Ⅱ）若过 $T (4 ， 0)$ 且互相垂直的直线 $l_{1}$ ， $l_{2}$ 分别与抛物线 $C$ 交于 $P$ ， $Q$ ， $R$ ， $S$ 四点，求四边形 $P Q R S$ 面积的最小值.

查看试题解析