广西来宾市兴宾区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期：2021-04-27 类型：期中考试
一、单选题
-
1. 下列图形中，属于中心对称图形的是（ ）A、
B、
C、
D、
2. 如果一个三角形的三个内角的度数之比为 ，那么这个三角形是（ ）A、锐角三角形 B、直角三角形 C、钝角三角形 D、锐角三角形或直角三角形3. 下列各组线段能构成直角三角形的是（ ）A、 B、 C、 D、4. 在▱ABCD中，∠A∶∠B∶∠C∶∠D的值可以是（ ）A、1∶2∶3∶4 B、1∶2∶2∶1 C、1∶1∶2∶2 D、2∶1∶2∶15. 矩形具有而平行四边形不一定具有的性质是（ ）A、对边平行且相等 B、对角相等 C、对角线互相平分 D、对角线相等6. 如图，AD∥BC，∠ABC的平分线BP与∠BAD的平分线AP相交于点P，作PE⊥AB于点E，若PE＝2，则两平行线AD与BC间的距离为（ ）
A、2 B、3 C、4 D、57. 一个多边形的内角和是它的外角和的2倍，则这个多边形是（ ）A、五边形 B、六边形 C、七边形 D、八边形8. 如图，菱形ABCD中，点E，F分别是AC，DC的中点，若EF=3，则菱形ABCD的周长是（ ）
A、12 B、16 C、20 D、249. 如图，在平行四边形ABCD中，按以下步骤作图：①以A为圆心，AB长为半径画弧，交边AD于点；②再分别以B，F为圆心画弧，两弧交于平行四边形ABCD内部的点G处；③连接AG并延长交BC于点E，连接BF，若BF＝3，AB＝2.5，则AE的长为（ ）
A、2 B、4 C、8 D、510. 如图，边长相等的两个正方形ABCD和OEFG，若将正方形OEFG绕点O按逆时针方向旋转150°，两个正方形的重叠部分四边形OMCN的面积（ ）
A、不变 B、先增大再减小 C、先减小再增大 D、不断增大11. 如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（ ）
A、2 B、 C、 D、12. 如图，在▱ABCD中，AD=2AB，F是AD的中点，作CE⊥AB，垂足E在线段AB上（E不与A，B重合），连接EF，CF，则下列结论中一定成立的是 （ ）
①∠DCF= ∠BCD；②EF=CF；③ ；④∠DFE=4∠AEF
A、①②③④ B、①②③ C、①② D、①②④二、填空题
-
13. 如图，一棵树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°夹角，这棵树在折断前的高度为米.
14. 如图，数轴上点A表示的数据为 ．
15.三个正方形的面积如图所示，则字母B所代表的正方形的面积是
16. 如图，DE是△ABC的中位线，点F在DE上，且∠AFB=90°，AB=6，BC=10，则EF= ．
17. 如图，在矩形ABCD中，点E在边CD上，将矩形ABCD沿AE所在直线折叠，点D恰好落在边BC上的点F处.若AB=8，DE=5，则折痕AE的长为.
18. 如图，菱形 的对角线交于点 是线段 上一动点， E 是线段 AB上一个动点，则 的最小值为 .
三、解答题
-
19. 如图， ， ， 、 相交于点 .求证： .
20. 如图，▱ABCD的对角线AC、BD相交于点O，AE＝CF.求证：BE＝DF.
21. 如图，在四边形 中， ， ， ，且 于B.求四边形 的面积.
22. 如图，在Rt△ABC中，∠BAC＝90°，AD平分∠BAC，过AC的中点E作FG∥AD，交BA的延长线于点F，交BC于点G，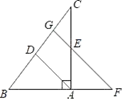
(1)、求证：AE＝AF；(2)、若BC＝ AB，AF＝3，求BC的长.23. 在平行四边形ABCD中，连接AC、BD交于点O，点E为AD的中点，连接CE并延长交于BA的延长线于点F，连接DF.
(1)、求证：四边形ACDF是平行四边形；(2)、若AD＝2AB，∠ABC＝60°，试判断四边形ACDF的形状，并说明理由.24. 如图，在△ABC中，AB=AC，AD ⊥BC，垂足为点D，AN是△ABC外角∠CAM的平分线，CE ⊥AN，垂足为点E．
(1)、求证：四边形ADCE为矩形；(2)、当△ABC满足什么条件时，四边形ADCE是一个正方形?并给出证明．25. 如图，在矩形ABCD中，BC＝4，AB＝10，E为CD边上的一点，DE＝7，动点P从点A出发，以每秒1个单位的速度沿着边AB向终点B运动，连接PE.设点P运动的时间为t秒.
(1)、求BE的长；(2)、当t为多少秒时，△BPE是直角三角形？26. 如图①，已知点O为正方形 的对角线的交点，点P是对角线 上的一个动点（点P不与 重合），分别过点 向直线 作垂线，垂足分别为点 ，连接 和 .
(1)、求证： ；(2)、如图②，延长正方形对角线 ，当点P运动到 的延长线上时，通过证明判断（1）中的结论是否仍然成立；(3)、若点P在射线 上运动， ，求线段 的长.