广西贺州市平桂区2019-2020学年八年级下学期数学期中考试试卷
试卷更新日期:2021-04-27 类型:期中考试
一、单选题
-
1. 下列各式是一元二次方程一般形式的是( ).A、 B、 C、 D、2. 若二次根式 在实数范围内有意义,则x的取值范围是( ).A、 B、 C、 D、3. 下列三边的长不能成为直角三角形三边的是( )A、3,4,5 B、4,5,6 C、6,8,10 D、5,12,134. 下列式子中,属于最简二次根式的是( ).A、 B、 C、 D、5. 用公式法解一元二次方程 ,对应a,b,c的值分别为( ).A、0,4,3 B、1,4,-3 C、1,4, 3 D、1,-4,36. 下列各式计算正确的是( ).A、 B、 C、 D、7. 方程x(x﹣1)=0的根是( )A、x=0 B、x=1 C、x1=0,x2=1 D、x1=0,x2=﹣18. 在Rt△ABC中,∠C=90°,AC=2,∠B=30°,则BC为( ).A、1 B、 C、 D、49. 下列一元二次方程不适合用因式分解法解方程的是( ).A、 B、 C、 D、10. 对于实数a,如果 ,那么下列结论正确的是( ).A、 B、 C、 D、11. 某公司今年销售一种产品,一月份获得利润10万元,由于产品畅销,利润逐月增加,一季度共获利36.4万元,已知2月份和3月份利润的月增长率相同.设2,3月份利润的月增长率为x,那么x满足的方程为( )A、10(1+x)2=36.4 B、10+10(1+x)2=36.4 C、10+10(1+x)+10(1+2x)=36.4 D、10+10(1+x)+10(1+x)2=36.412. 如图,在平面直角坐标系中,直线l是y=x的图象,点 在x轴正半轴上, .作 交直线l于点 ,以O为圆心, 为半径画弧,交x轴正半轴于点 .作 交直线l于点 ,以O为圆心, 为半径画弧,交x轴正半轴于点 .作 交直线l于点 ,以O为圆心, 为半径画弧,交x轴正半轴于点 …….按此作法进行下去,则点 的横坐标为( ).
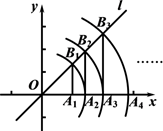 A、 B、 C、 D、
A、 B、 C、 D、二、填空题
-
13. 比较大小:14. 已知关于x的方程 是一元二次方程,则k=.15. 已知△ABC的三边长分别是1、2、 ,则△ABC的面积为;16. 已知等腰三角形的边长是方程 的两个根,则此三角形的周长为.17. 计算: .18. 如图,矩形纸片ABCD中,AB=4,BC=6,将△ABC沿AC折叠,使点B落在点E处,CE交AD于点F,则DF的长等于 .
 19. 形如 的方程的图解法:画Rt△ABC(如图),使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= ,则该方程的一个根就是AD的长.
19. 形如 的方程的图解法:画Rt△ABC(如图),使∠ACB=90°,BC= ,AC=b,再在斜边AB上截取BD= ,则该方程的一个根就是AD的长. (1)、如下是证明过程:
(1)、如下是证明过程:请阅读并填空:配方 ,
,
.
∵∠ACB=90° ,∴
∵AC=b,BC= , AB=AD+
∴ , ∴
∴ , 取 , 即
(2)、如果利用此图解法解方程 ,那么AC= , BC= , 方程的一个根是.三、解答题
-
20. 计算:(1)、(2)、21. 用适当的方法解下列方程:(1)、(2)、22. 已知关于x的方程 有实数根.(1)、求m的取值范围;(2)、若方程的一根为1,求m的值.23. 已知a、b、c满足(1)、求a、b、c的值.(2)、试问:以a、b、c为三边长能否构成三角形,如果能,请求出这个三角形的周长,如不能构成三角形,请说明理由.24. 在一次消防演习中,消防员架起一架25米长的云梯AB,如图斜靠在一面墙上,梯子底端B离墙角C的距离为7米。
 (1)、求这个梯子的顶端距地面的高度AC是多少?(2)、如果消防员接到命令,按要求将梯子底部在水平方向滑 动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?25. 商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)、若每台冰箱降价150元,则平均每天可售出台冰箱;(2)、商场要想在这种冰箱销售中平均每天盈利4800元,要使百姓得到实惠,每台冰箱应降价多少元?26. 如图,在△ABC中,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以1.5cm/s的速度移动,在B点停止,点P,Q分别从A、C同时出发4秒钟后PQ= cm.
(1)、求这个梯子的顶端距地面的高度AC是多少?(2)、如果消防员接到命令,按要求将梯子底部在水平方向滑 动后停在DE的位置上(云梯长度不变),测得BD长为8米,那么云梯的顶部在下滑了多少米?25. 商场将进价为2000元的冰箱以2400元售出,平均每天能售出8台,为了配合国家“家电下乡”政策的实施,商场决定采取适当的降价措施.调查表明:这种冰箱的售价每降低50元,平均每天就能多售出4台.(1)、若每台冰箱降价150元,则平均每天可售出台冰箱;(2)、商场要想在这种冰箱销售中平均每天盈利4800元,要使百姓得到实惠,每台冰箱应降价多少元?26. 如图,在△ABC中,AC=6cm,BC=8cm,点P从A沿AC边向C点以1cm/s的速度移动,在C点停止,点Q从C点开始沿CB边向点B以1.5cm/s的速度移动,在B点停止,点P,Q分别从A、C同时出发4秒钟后PQ= cm. (1)、求证:∠ACB=90°;(2)、若点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ.
(1)、求证:∠ACB=90°;(2)、若点P、Q分别从A、C同时出发,经过几秒钟后PQ=BQ.