广西崇左市大新县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 要使二次根式 $\sqrt{x + 1}$ 有意义，字母x的取值必须满足（）

A、 $x \geq 0$ B、 $x \leq 0$ C、 $x \geq 1$ D、 $x \geq - 1$

查看试题解析
2. 下列二次根式中，最简二次根式是（）

A、 $\sqrt{x^{2} - y^{2}}$ B、 $\sqrt{\frac{1}{2}}$ C、 $\sqrt{24}$ D、 $\sqrt{2 a^{2}}$

查看试题解析
3. 下列计算中，正确的是（　　）

A、 $2 \sqrt{3}$ + $3 \sqrt{2}$ = $5 \sqrt{5}$ B、 $3 \sqrt{3}$ × $2 \sqrt{3}$ =3 $\sqrt{6}$ C、 $\sqrt{27}$ ÷ $\sqrt{3}$ =3 D、 $\sqrt{{(- 3)}^{2}}$ =﹣3

查看试题解析
4. 方程 $x^{2} - 4 x = 0$ 的解是（）

A、 $x = 4$ B、 $x = 2$ C、 $x_{1} = 4, x_{2} = 0$ D、 $x = 0$

查看试题解析
5. 用配方法将方程 $x^{2} + 6 x - 11 = 0$ 变形为（）

A、 ${(x - 3)}^{2} = 20$ B、 ${(x + 3)}^{2} = 20$ C、 ${(x + 3)}^{2} = 2$ D、 ${(x - 3)}^{2} = 2$

查看试题解析
6. 已知关于 $x$ 的一元二次方程 $(a - 1) x^{2} - 2 x + 1 = 0$ 有实数根，则 $a$ 的取值范围是（）

A、 $a \leq 2$ B、 $a > 2$ C、 $a \leq 2$ 且 $a \neq 1$ D、 $a < - 2$

查看试题解析
7. 已知一个直角三角形的两边长分别3和4，则第三边长是（）

A、5 B、 $\sqrt{7}$ C、25 D、5或 $\sqrt{7}$

查看试题解析
8. 已知方程 $2 x^{2} + 6 x - 1 = 0$ 的两个实数根为 $x_{1}, x_{2}$ ，则 $\frac{1}{x_{1}} + \frac{1}{x_{2}}$ 的值为（）

A、-3 B、3 C、6 D、-6

查看试题解析
9. 某超市一月份的营业额是100万元，月平均增加的百分率相同，第一季度的总营业额是364万元，若设月平均增长的百分率是x，那么可列出的方程是（）

A、 $100 {(1 + x)}^{2} = 364$ B、 $100+100 (1 + x) + 100 {(1 + x)}^{2} = 364$ C、 $100 {(1 + 2 x)}^{2} = 364$ D、 $100+100 (1 + x) + 100 {(1 + 2 x)}^{2} = 364$

查看试题解析
10. 如图，在Rt△ABC中，∠ACB＝90°，AE为△ABC的角平分线，且ED⊥AB，若AC＝6，BC＝8，则BD的长（　　）

A、2 B、3 C、4 D、5

查看试题解析
11. 直线 $l ： y = (m - 3) x - 2 + n$ （m，n为常数）的图象如图，化简︱ $m - 3$ ︱－ $\sqrt{n^{2} - 4 n + 4}$ 得（）

A、 $5 - m - n$ B、 $n - m + 1$ C、 $m - n - 1$ D、 $m + n - 5$

查看试题解析
12. △ABC的三边分别为 $a, b, c$ ，下列条件能推出△ABC是直角三角形的有（）
① $a^{2} - c^{2} = b^{2}$ ;② $(a - b) (a + b) + c^{2} = 0$ ;③ ∠A＝∠B $-$ ∠C; ④∠A∶∠B∶∠C＝1∶2∶3 ;⑤ $a = \frac{1}{3}, b = \frac{1}{4}, c = \frac{1}{5}$ ;⑥ $a = 10,$ $b = 24,$ $c = 26$

A、2个 B、3个 C、4个 D、5个

查看试题解析

二、填空题

13. 计算 $\sqrt{48} - \sqrt{12}$ 的结果是.

查看试题解析
14. 如图，在一个高为5m ，长为13m的楼梯表面铺地毯，则地毯的长度至少是．

查看试题解析
15. $\sqrt{27}$ 与最简二次根式 $\sqrt{m + 1}$ 是同类二次根式，则m＝.

查看试题解析
16. 等腰三角形的顶角为 $120 °$ ，底边上的高为2，则它的周长为.

查看试题解析
17. 若关于x的一元二次方程 $(m - 1) x^{2} + 5 x + m^{2} + 3 m - 6 = 0$ 的常数项为-2，则m的值为.

查看试题解析
18. 若关于x的方程 $a x^{2} + 2 (a - b) + (b - a) x = 0$ 有两个相等的实数根，则a：b＝.

查看试题解析

三、解答题

19. 计算：

(1)、 $\sqrt{18} - 4 \sqrt{\frac{1}{2}} + \sqrt{24} \div \sqrt{3}$ 　　　　　　　

(2)、 $\sqrt{2} \times (\sqrt{2} + \frac{1}{\sqrt{2}}) - \frac{\sqrt{18} - \sqrt{8}}{\sqrt{2}}$

查看试题解析
20. 解下列方程：

(1)、 $x^{2} - 9 = 4 (x - 3)$

(2)、 $3 x^{2} - x = 1$

查看试题解析
21. 已知： $a = \sqrt{2} - 1, b = \sqrt{2} + 1$ ，求：

(1)、a－b的值；

(2)、ab的值；

(3)、 $\frac{a}{b} - \frac{b}{a}$ 的值.

查看试题解析
22. 如图，在4x4的正方形网格中，每个小正方形的边长都为1.

求：

(1)、△ABC的周长；

(2)、∠ABC度数.

查看试题解析
23. 已知关于x的方程 $x^{2} + 2 k x + k^{2} - 1 = 0$ .

(1)、试说明：无论k取何值时，方程总有两个不相等的实数很；

(2)、如果方程有一个根为-3，试求 $2 k^{2} + 12 k + 2019$ 的值.

查看试题解析
24. 一架梯子AB长25米，如图斜靠在一面墙上，梯子底端B离墙7米．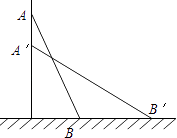

(1)、这个梯子的顶端距地面有多高？

(2)、如果梯子的顶端下滑了4米，那么梯子底部在水平方向滑动了4米吗？为什么？

查看试题解析
25. 已知a，b，c是△ABC的三边长，关于x的一元二次方程 $x^{2} + 2 \sqrt{b} x + 2 c = 0$ 有两个相等的实数根，关于x的方程3cx+2b＝2a的根为x＝0.

(1)、试判断△ABC的形状;

(2)、若a，b是关于x的一元二次方程 $x + m x - 3 m = 0$ 的两个实数根，求m的值.

查看试题解析
26. 某商场计划购进一批书包，经市场调查发现：某种进货价格为30元的书包以40元的价格出售时，平均每月售出600个，并且书包的售价每提高1元，某月销售量就减少10个.

(1)、若售价定为42元，每月可售出多少个？

(2)、若书包的月销售量为300个，则每个书包的定价为多少元？

(3)、当商场每月有10000元的销售利润时，为体现“薄利多销”的销售原则，你认为销售价格应定为多少？

查看试题解析