广西百色市田东县2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 计算 $\sqrt{4}$ 的结果是（）

A、 $\pm 2$ B、2 C、 $- 2$ D、4

查看试题解析
2. 直角三角形的两直角边长分别为1、 $\sqrt{3}$ ，则斜边长为（）

A、2 B、 $\sqrt{3}$ C、 $\sqrt{3} + 1$ D、4

查看试题解析
3. 方程 $x (x + 1) = 0$ 的两个根是（）

A、x₁=0，x₂=1 B、x₁=0，x₂=-1 C、x₁=0，x₂=0 D、x₁=1，x₂=-1

查看试题解析
4. $\sqrt{x - 2}$ 在实数范围内有意义，则x的取值范围是（）

A、x≥2 B、x＞2 C、 $x = 2$ D、x＜2

查看试题解析
5. 下面运算正确的是

A、 $\sqrt{2} + \sqrt{3} = \sqrt{5}$ B、 $\sqrt{2} \times \sqrt{3} = \sqrt{5}$ C、 $\sqrt{8} - 2 = 0$ D、 $\sqrt{12} \div \sqrt{3} = 2$

查看试题解析
6. 下列命题中，错误的命题是（）

A、 $2 \sqrt{10}$ 是最简二次根式 B、方程 $x^{2} + \sqrt{3} x + 1 ＝ 0$ 没有实数根 C、直角三角形两直角边的平方和等于斜边的平方 D、 $\sqrt{{(1 - \sqrt{2})}^{2}} = 1 - \sqrt{2}$

查看试题解析
7. 用配方法解方程 $x^{2} - 3 x - 2 = 0$ 时，该方程可变形为（）

A、 ${(x - \frac{3}{2})}^{2} = \frac{1}{4}$ B、 ${(x - \frac{3}{2})}^{2} = \frac{17}{4}$ C、 ${(x - 3)}^{2} = 2$ D、 ${(x - 3)}^{2} = 11$

查看试题解析
8. 一个长方体的体积是 $\sqrt{48} c m^{3}$ ，长是 $\sqrt{6} c m$ ，宽是 $\sqrt{2} c m$ ，则它的高是（）

A、 $4 c m$ B、 $\sqrt{3} c m$ C、 $2 \sqrt{2} c m$ D、 $2 c m$

查看试题解析
9. 一艘轮船和一艘渔船同时沿各自的航向从港口O出发，如图所示，轮船从港口O沿北偏西20°的方向行60海里到达点M处，同一时刻渔船已航行到与港口O相距80海里的点N处．若M，N两点相距100海里，则∠NOF的度数为（）

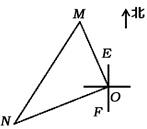A、50° B、60° C、70° D、90°

查看试题解析
10. 若x＝－2是关于x的一元二次方程x²＋ $\frac{3}{2}$ ax－a²＝0的一个根，则a的值为（）

A、1或-4 B、－1或－4 C、-1或4 D、1或4

查看试题解析
11. 我国南宋著名数学家秦九韶的著作《数书九章》里记载有这样一道题：“问有沙田一块，有三斜，其中小斜五里，中斜十二里，大斜十三里，欲知为田几何？”这道题讲的是：有一块三角形沙田，三条边长分别为5里，12里，13里，问这块沙田面积有多大？题中“里”是我国市制长度单位，1里=500米，则该沙田的面积为（）

A、7.5平方千米 B、15平方千米 C、75平方千米 D、750平方千米

查看试题解析
12. $\sqrt{10}$ 的整数部分是x，小数部分是y，则y（x+ $\sqrt{10}$ ）的值是（）

A、1 B、2 C、3 D、4

查看试题解析

二、填空题

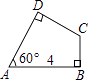
13. 在实数范围内分解因式：m²﹣2＝．

查看试题解析
14. 关于x的一元二次方程 $4 x^{2} - (a + 2) x + a - 1 = 0$ 有两个相等的实数根，则 $a =$ .

查看试题解析
15. 两直角边长分别为 $2 \sqrt{3} + 1$ ， $2 \sqrt{3} - 1$ 的三角形的面积是.

查看试题解析
16. 如图，在四边形ABCD中，∠B=∠D=90°，∠A=60°，AB=4，则AD的取值范围是．

查看试题解析
17. $\sqrt{9 \times 9 + 19} = \sqrt{9 \times 9 + 9 + 10} = \sqrt{9 \times (9 + 1) + 10} = \sqrt{10 \times 10} = 10$ ，那么 $\sqrt{\underset{2020 个 9}{\underset{�}{99 \dots 9}} \times \underset{2020 个 9}{\underset{�}{99 \dots 9}} + 1 \underset{2020 个 9}{\underset{�}{99 \dots 9}}}$ = .

查看试题解析

三、解答题

18. 计算： ${(- 2)}^{3} \times \frac{1}{8} + (\sqrt{27} - \sqrt{12}) \div \sqrt{3}$

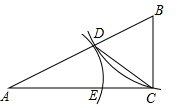
查看试题解析
19. 用适当的方法解方程： $x^{2} + 2 x + 2 = 5$

查看试题解析
20. 在直角三角形ABC中，∠C=90°，AC＝2，BC= $2 \sqrt{3}$ ，求AB边上的高CD是多少.

查看试题解析
21. 已知 $x = \frac{1}{2} (\sqrt{2} + 1)$ ， $y = \frac{1}{2} (\sqrt{2} - 1)$ ，求代数式 $x^{2} - x y + y^{2}$ 的值.

查看试题解析
22. 用配方法解关于x的方程： $x^{2} + p x + q = 0$

查看试题解析
23. 在直角墙角AOB（OA⊥OB，且OA、OB长度不限）中，要砌20m长的墙，与直角墙角AOB围成地面为矩形的储仓，且地面矩形AOBC的面积为96m².

(1)、求这地面矩形的边长；

(2)、有规格为0.80×0.80和1.00×1.00（单位：m）的地板砖单价分别为55元/块和80元/块，若只选其中一种地板砖都恰好能铺满储仓的矩形地面（不计缝隙），用哪一种规格的地板砖费用较少？

查看试题解析
24. 一艘轮船以16n mile/h的速度离开港口向东南方向航行，另一艘轮船在同时同地以12n mile/h的速度向西南方向航行，它们在离开港口1.5h后相距多远？

查看试题解析
25. 如图，在△ABC中，∠ACB＝90°，以点B为圆心，BC长为半径画弧，交线段AB于点D；以点A为圆心，AD长为半径画弧，交线段AC于点E，连结CD.

(1)、若∠A＝28°，求∠ACD的度数.

(2)、设BC＝a，AC＝b.
①线段AD的长是方程x²+2ax﹣b²＝0的一个根吗？说明理由.

②若AD＝EC，求 $\frac{a}{b}$ 的值.

查看试题解析