福建省南平市2019-2020学年八年级下学期数学期中考试试卷

试卷更新日期：2021-04-27 类型：期中考试

进入出卷网下载

一、单选题

1. 下列各式： $\sqrt{3}$ ， $\sqrt{x^{2}}$ ， $\sqrt[3]{2}$ ， $\sqrt{x + 2} (x \geq - 2)$ 其中二次根式的个数为(　　)

A、 $1$ B、 $2$ C、 $3$ D、 $4$

查看试题解析
2. 下列四组线段中，可以构成直角三角形的是（　　）

A、4，5，6 B、1.5，2，2.5 C、2，3，4 D、1， $\sqrt{2}$ ， 3

查看试题解析
3. 下列计算正确的是(　　)

A、 $\sqrt{- 3^{2}} = 9$ B、 ${(\sqrt{3})}^{2} = 3$ C、 $\sqrt{{(- 3)}^{2}} = - 3$ D、 $\sqrt{3^{2}} = 9$

查看试题解析
4. 杨伯家小院子的四棵小树E、F、G、H刚好在其四边形院子 $A B C D$ 各边的中点上，若在四边形 $E F G H$ 内种上小草，则这块草地的形状是(　　)

A、平行四边形 B、矩形 C、正方形 D、菱形

查看试题解析
5. 下列命题中，真命题的是（）

A、对角线互相垂直的四边形是菱形 B、对角线互相垂直平分的四边形是正方形 C、对角线相等的四边形是矩形 D、对角线互相平分的四边形是平行四边形

查看试题解析
6. 如图，在▱ABCD中，AC、BD为对角线，BC＝6，BC边上的高为4，则阴影部分的面积为（）

A、3 B、6 C、12 D、24

查看试题解析
7. 如图，已知在 $R t △ A B C$ 中， $∠ A C B = 90 ° ， A B = 8$ ，分别以 $A C ， B C$ 为直径作半圆，面积分别记为 $S_{1} ， S_{2}$ ，则 $S_{1} + S_{2}$ 等于(　　)

A、 $2 π$ B、 $4 π$ C、 $6 π$ D、 $8 π$

查看试题解析
8. 计算： ${(2 + \sqrt{3})}^{9} \times {(2 - \sqrt{3})}^{10} =$ (　　)

A、 $2 + \sqrt{3}$ B、 $2 - \sqrt{3}$ C、 $- 2 + \sqrt{3}$ D、 $- 2 - \sqrt{3}$

查看试题解析
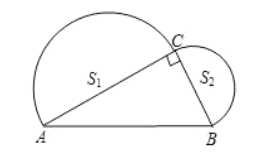9. 用四张大小一样的长方形纸片拼成一个正方形 $A B C D$ (如图)，它的面积是 $48 ，$ 已知长方形的一边长 $A E = 3 \sqrt{3} ，$ 图中空白部分是一个正方形，则这个小正方形的周长为(　　)

A、 $2 \sqrt{3}$ B、 $4 \sqrt{3}$ C、 $8 \sqrt{3}$ D、 $16 \sqrt{3}$

查看试题解析
10. 如图所示，在矩形 $A B C D$ 中， $A B = 12 ， A C = 20$ ，两条对角线相交于点O.以 $O B 、 O C$ 为邻边作第 $1$ 个 $▱ O B B_{1} C$ ，对角线相交于点 $A_{1}$ ，再以 $A_{1} B_{1}$ 、 $A_{1} C$ 为邻边作第 $2$ 个 $▱ A_{1} B_{1} C_{1} C$ ，对角线相交于点 $O_{1}$ ；再以 $O_{1} B_{1}$ 、 $O_{1} C_{1}$ 为邻边作第 $3$ 个 $▱ O_{1} B_{1} B_{2} C_{1}$ ……依此类推.则第 $6$ 个平行四边形的面积为(　　)

A、 $6$ B、 $15$ C、 $3$ D、 $12$

查看试题解析

二、填空题

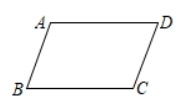
11. 若二次根式 $\sqrt{x - 2}$ 有意义，则x的取值范围是．

查看试题解析
12. 若实数a、b满足 $| a + 2 | + \sqrt{b - 4} = 0$ ，则 $\frac{a}{b}$ = ．

查看试题解析
13. 若菱形的两条对角线长分别是6㎝和8㎝，则该菱形的面积是㎝² ．

查看试题解析
14. 如图，在平行四边形 $A B C D$ 中，添加一个条件，使平行四边形 $A B C D$ 是矩形.

查看试题解析
15. 如图，把矩形纸片 $A B C D$ 沿 $E F$ 折叠，使点B落在边 $A D$ 上的点 $B^{'}$ 处，点A落在点 $A^{'}$ 处，已知 $A D = 10 ， C D = 4 ， B^{'} D = 2$ .则 $A E =$ .

查看试题解析
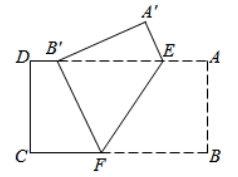16. 如图，小明在A时测得某树的影长为2m，B时又测得该树的影长为8m，若两次日照的光线互相垂直，则树的高度为m．

查看试题解析

三、解答题

17. 计算：

(1)、 $\sqrt{5} + \sqrt{45} - \sqrt{20}$

(2)、 $(2 \sqrt{2} + \sqrt{7}) (2 \sqrt{2} - \sqrt{7})$ .

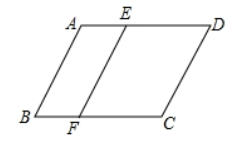
查看试题解析
18. 如图，在 $▱ A B C D$ 中，E、F分别在AD、BC上，且 $E F // A B$ .求证： $E F = C D$ .

查看试题解析
19. 如图，在 $△ A B C$ 中，AB=BC，D、E、F分别是BC、AC、AB边上的中点.

(1)、求证：四边形 $B D E F$ 是菱形.

(2)、若 $A B = 10 c m ，$ 求四边形 $B D E F$ 的周长.

查看试题解析
20. 某学校要对如图所示的一块地进行绿化，已知 $A D = 4 m$ ， $C D = 3 m$ ， $A D ⊥ D C$ ， $A B = 13 m$ ， $B C = 12 m$ ，求这块地的面积.

查看试题解析
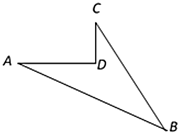21. 如图所示， $A B C D$ 是一个正方形花园，E，F是它的两个门，且 $D E = C F$ .要修建两条路 $B E$ 和 $A F$ ，这两条路等长吗？它们有什么位置关系？为什么？

查看试题解析
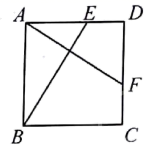22. 问题背景：在△ABC中，AB、BC、AC三边的长分别为 $\sqrt{5}$ 、 $\sqrt{10}$ 、 $\sqrt{13}$ ，求这个三角形的面积小辉同学在解答这道题时，先建立一个正方形网格（每个小正方形的边长为1），再在网格中画出格点△ABC（即△ABC三个顶点都在小正方形的顶点处），如图1所示.这样不需求△ABC的高，而借用网格就能计算出它的面积.

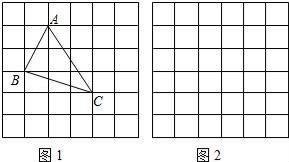(1)、请你利用上述方法求出△ABC的面积.

(2)、在图2中画△DEF，DE、EF、DF三边的长分别为 $\sqrt{2}$ 、 $\sqrt{8}$ 、 $\sqrt{10}$
①判断三角形的形状，说明理由.

②求这个三角形的面积.（直接写出答案）

查看试题解析
23. 如图，在四边形 $A B C D$ 中，连接AC、BD，已知 $∠ A C B = ∠ A D B = 90 ° ，$ 且点 $E ， F$ 分别为AB、CD的中点，连接 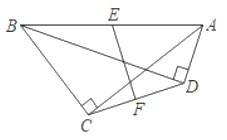$E F$ .

(1)、求证： $E F ⊥ C D$ .

(2)、若 $A B = 2 C D = 6$ ，求 $E F$ 的长.

查看试题解析
24. 先阅读下列材料，再解决问题：我们定义一组对边平行，另一组对边不平行的四边形叫做梯形，其中平行的两边叫梯形的底边，不平行的两边叫梯形的腰，连接梯形两腰中点的线段叫梯形的中位线.
如图， $E ， F$ 分别是梯形 $A B C D$ 的两腰 $A B$ 和 $C D$ 的中点，即 $E F$ 为梯形 $A B C D$ 的中位线.请同学们思考梯形的中位线与两底有何数量关系与位置关系？并给予证明.

猜想：

已知：

求证：

证明：

查看试题解析
25. 如图所示，在四边形 $A B C D$ 中， $A D // B C ， ∠ A = 90 °$ ， $A B = 12 ， B C = 21 ， A D = 16$ .动点P从点B出发，沿射线 $B C$ 方向以每秒 $2$ 个单位长度的速度运动，动点Q同时从点A出发，在线段 $A D$ 上以每秒 $1$ 个单位长度的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动.设运动的时间为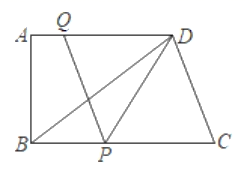 $t$ 秒.

(1)、填空： $A Q =$ ； $B P =$ ；t的取值范围是.

(2)、设 $△ D P Q$ 的面积为S，请用含t的式子表示S.

(3)、当 $t =$ 时， $P D = P Q$ .

(4)、当t为何值时，以点 $P ， C ， D ， Q$ 为顶点的四边形是平行四边形.

查看试题解析